The scenario:
In the depths of the Plane of Shadow stands Lacc, an ancient, unimaginably vast city inhabited by restless shades and creatures of darkness. This City of Monoliths consumes entire worlds, incorporating each world into itself as the monoliths that give Lacc its nickname grind their way across the landscape, expanding like a growing ink-stain upon a planet’s surface.
The important question, of course, is: how should I model this process mathematically?
The scenario described above comes from an adventure module called “Gates of Oblivion” (by Alec Austin), written for D&D 3.5, and published in Dungeon magazine #136. The module states that “The area consumed by Lacc expands at a rate of half a mile per hour”. This is clear enough, but: (a) it’s entirely the wrong sort of rate function for the needs of the adventure; (b) it’s much too arbitrary; and (c) it’s much too straightforward and thus boring.
Elaborating on each of these (click to expand):
The wrong rate function. In my adaptation of this module, Tenaris Xin (ruler of the City of Monoliths) is carrying out a ritual that, if completed, will incorporate the world of the player characters (a.k.a. “PCs”) into Lacc. Xin begins the ritual when Lacc makes contact with the PCs’ world (and the PCs should learn of Lacc’s incursion shortly thereafter); the completion date should (from a design standpoint) be far enough into the future that the PCs have time to hear about the strange zone of darkness which has begun to spread across the land, investigate, take some time to explore Lacc, discover the nature of the threat, and finally carry out a successful raid of Xin’s redoubt to stop the ritual and save their world. A reasonable time scale would be somewhere between a week and a month (probably closer to the latter); shorter, and it’s too easy for the PCs to end up feeling like they never had a chance and were set up to fail, while a longer time scale would undermine the sense that doom approaches and it’s up to the PCs to stop it.
Now, the adventure as written lacks the “ritual to be completed in a certain time period” aspect; instead, Tenaris Xin is totally passive (he’s basically just waiting in his tower for the PCs to show up and kill him), and Lacc is an automatic threat—it expands at the aforementioned fixed rate, and will eventually (at an absolutely predictable time) consume everything that the PCs value, if not stopped. When is “eventually”? Well, Lacc’s placement (see below) determines when any particular city or other locale of interest is consumed, but the entire world (assuming an Earth-sized planet) will take almost three years to fully incorporate. That is simultaneously too fast and too slow: too fast, because it means that there’s no need for any active measures on Xin’s part (consistent with the adventure as presented—Xin can just sit back and wait), but too slow, because a time scale of years makes it hard to have any sense of urgency about the problem.
The other problem with a fixed half-mile-per-hour rate of radius increase is that it can make Lacc’s placement feel arbitrary.
Too arbitrary. That is: where on the planet’s surface should Lacc’s incursion begin? From an authorial standpoint the answer is obviously “wherever the DM wants it to”, but what motivates the choice, and how will that choice appear both to the PCs’ (from an in-character perspective) and to the players (from a metagame perspective)? For instance, if the zone of darkness starts 100 miles away from the city of Greyhawk, then Lacc will consume Greyhawk exactly 200 hours after it arrives. What that looks like to the PCs is nothing: it’s an apparently arbitrary location. (If Xin were targeting Greyhawk for early assimilation, surely he could’ve aimed better? What’s a hundred miles away? Nothing in particular…) What it looks like to the players, meanwhile, is that the DM has decided, by fiat, that their characters have 200 hours to complete the adventure, and has placed Lacc’s point of contact accordingly. That’s not great for immersion and roleplaying.
Too straightforward. Every aspect of a well-designed adventure should contribute to feel of it, the atmosphere; the perceived theme should be consistent. The City of Monoliths should feel like something vast and ancient and powerful, lurking at the edge of comprehension, existing on a scale that daunts even high-level characters. Lacc’s rate of expansion, trivial a detail though it may seem, should serve that thematic purpose. It should seem to the players like there is a reason why it is thus and not otherwise, some mystery which they could perhaps unravel (though they don’t necessarily need to do so to achieve their goals), and that reason should play into the sense of Lacc’s otherworldly vastness.
The “half a mile per hour” fixed radius growth rate clearly fails to serve this purpose. It is obviously arbitrary; there’s no reason why it should be that, and not some other number; indeed, there’s no reason for a fixed radius growth rate at all. It’s immediately clear that there’s no deeper sense behind it. It’s not the most severe design sin, but we can do better.
Importantly, simply changing the rate of expansion wouldn’t fix these problems—if it’s a mile of radius growth per hour, or a mile per day, or ten miles per hour, the trouble is much the same. (The details would change: at ten miles per hour, the entire planet is consumed within just under two months, and an entire continent within perhaps 1–2 weeks. This is much too fast; it gives the PCs no chance to truly win, unless the point of origin for Lacc’s incursion is placed on some uninhabited continent. A rate could be found that will give the PCs just enough time… but the problems of arbitrariness and straightforwardness remain unchanged.) The rate function must be different. A linear rate of radius increase simply will not cut it.
What is the geometry of the Plane of Shadow?
Most planes (certainly including the Inner Planes) are said to be infinite in all directions (cf. the Manual of the Planes)—but how many directions is “all”? While considering this, I recalled certain suggestions (e.g. this blog post, Dragon magazine #8, #17, #38, etc.) that the planes exist in four spatial dimensions. This makes sense: if there’s only one Plane of Shadow, say, for all the Material Planes in existence (and such is indeed the canonical depiction of the planes in D&D), there will hardly be enough of it to contain everything that it would need to have (i.e., shadow reflections of Material Plane locations and inhabitants, for multiple—possibly infinitely many—Material Planes), if its dimensionality is no greater than that of a Material Plane.
This gave me the idea of modeling the manifestation of the City of Monoliths upon the Prime Material Plane as an intrusion of a four-dimensional object into a three-dimensional space. In this model, Lacc exists in four spatial dimensions, of which three are “lateral” (“north”, “south”, “east”, “west”, “kata”, “ana”) and one is the usual up–down. An incursion of Lacc onto the planet where our player characters reside will have the shape of an expanding hypersphere in four-dimensional space, the three-dimensional surface of which contains two “lateral” spatial dimensions and the one “vertical” dimension; at the point of contact with the PCs’ three-dimensional space, the contents of this surface will “flow” out into that space, the two “lateral” spatial dimensions of Lacc expanding onto the planet’s surface, and constituting the growing zone of darkness and inexorably advancing stone monoliths that the world’s inhabitants behold.
Consider first the one-dimension-lower analogue of the situation. We have two parallel planes (2D spaces), call them {$M$} and {$L$}, separated by a distance of {$d$} in the three-dimensional space within which they’re both embedded (figure 1); these are our analogues of the Prime Material Plane, and the city of Lacc in the Plane of Shadow, respectively. In {$M$} is a circle {$C_{M}$}; this is our analogue of a three-dimensional planet. (Note that the exterior of a circle is a finite one-dimensional space, just as the exterior of a sphere is a finite two-dimensional space.)
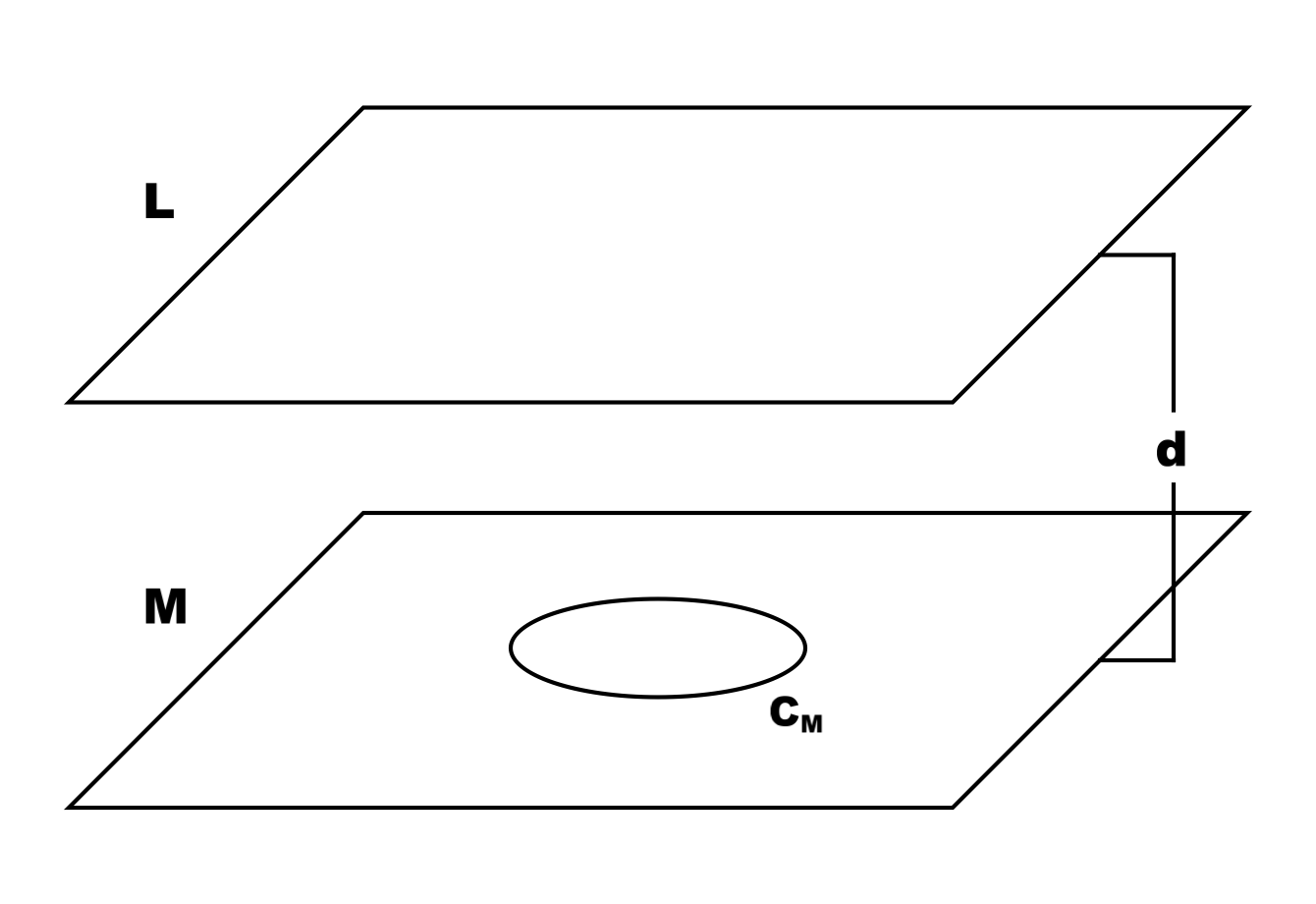
Figure 1. (Click to enlarge.)
At a point {$P_{M}$} on {$C_{M}$}, we construct a line, perpendicular to plane {$M$}; designate the point where this line intersects plane {$L$} as {$P_{L}$} (figure 2).
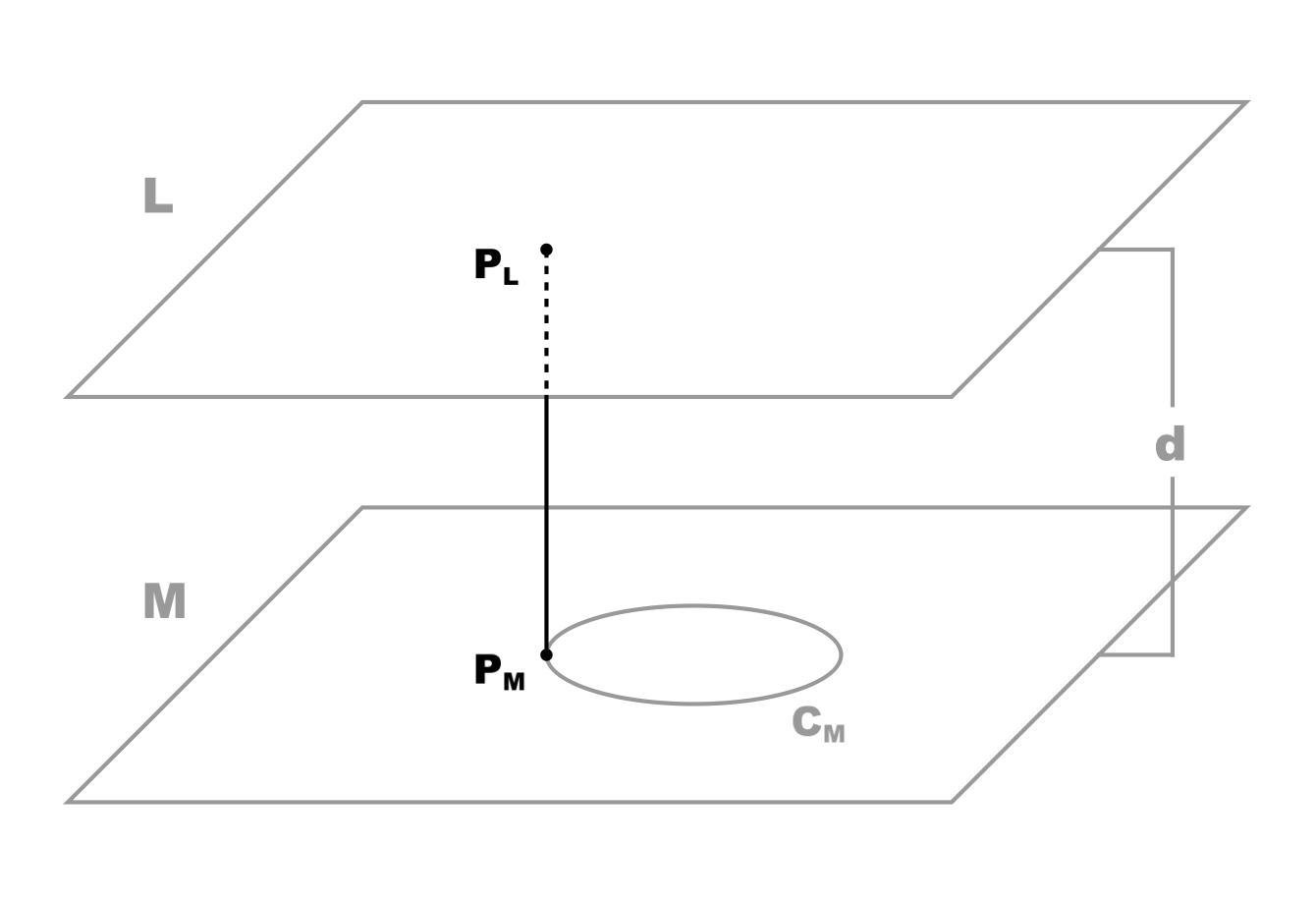
Figure 2. (Click to enlarge.)
The length of {$\overline{P_{M}P_{L}}$} is equal to {$d$}.
Now we construct a sphere {$S$}, centered at {$P_{L}$} (figure 3). The radius {$r_{S}$} of sphere {$S$} begins at 0 and increases as time passes, the increase going as the square root of time {$t$} (with a constant growth rate coefficient {$k$}). (Why the square root? We’ll come to that. Note that this naturally means that the surface area of {$S$}—which is proportional to the square of the radius—will increase linearly with {$t$}.)
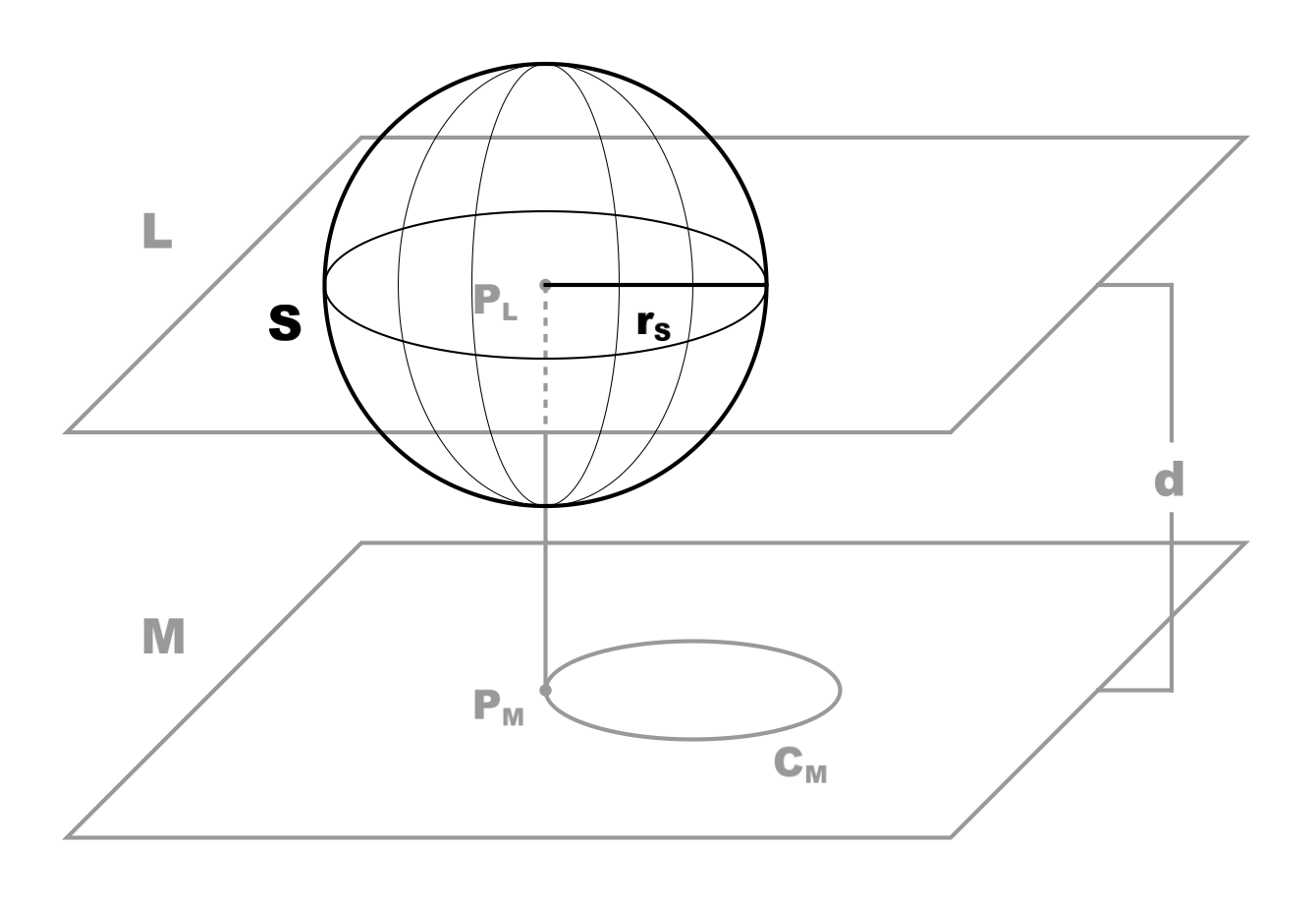
Figure 3. (Click to enlarge.)
Sphere {$S$} at some time {$0<t<t_{M}$}; {$0<r_{S}<d$}.
At some {$t_{M}$}, the radius {$r_{S}$} of sphere S will be equal to the distance {$d$} that separates planes {$M$} and {$L$}. At this time, {$S$} will be tangent to {$M$} (figure 4). The point of contact will of course be {$P_{M}$} (which, recall, is a point on the exterior of the circle {$C_{M}$} in plane {$M$}).
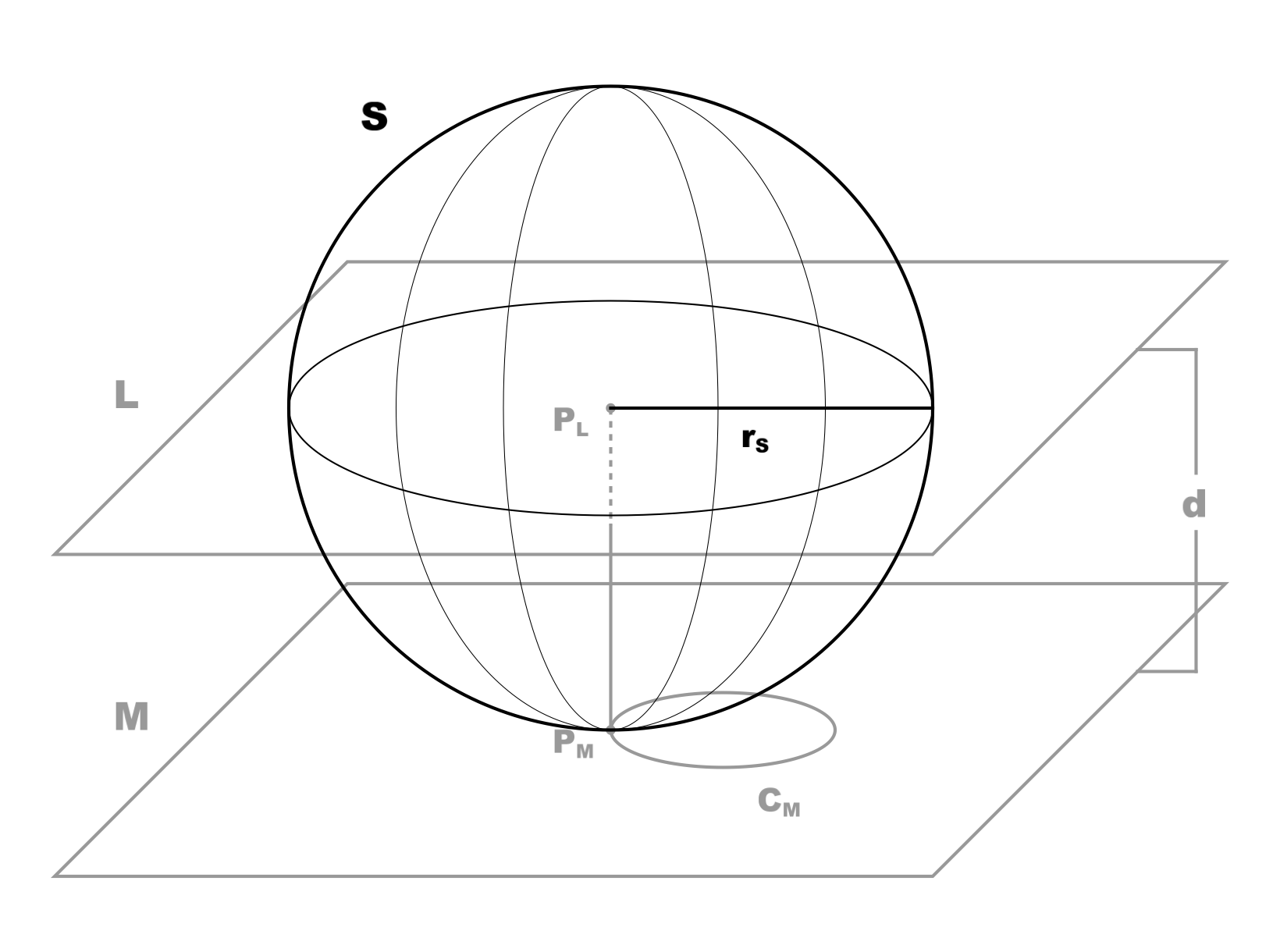
Figure 4. (Click to enlarge.)
Sphere {$S$} at {$t=t_{M}$}; {$r_{S}=d$}.
As time continues to pass and {$r_{S}$} keeps increasing, the sphere {$S$} will intersect plane {$M$}, which will cut off a spherical cap {$\mathit{CAP}_{S}$} (figures 5 and 6).
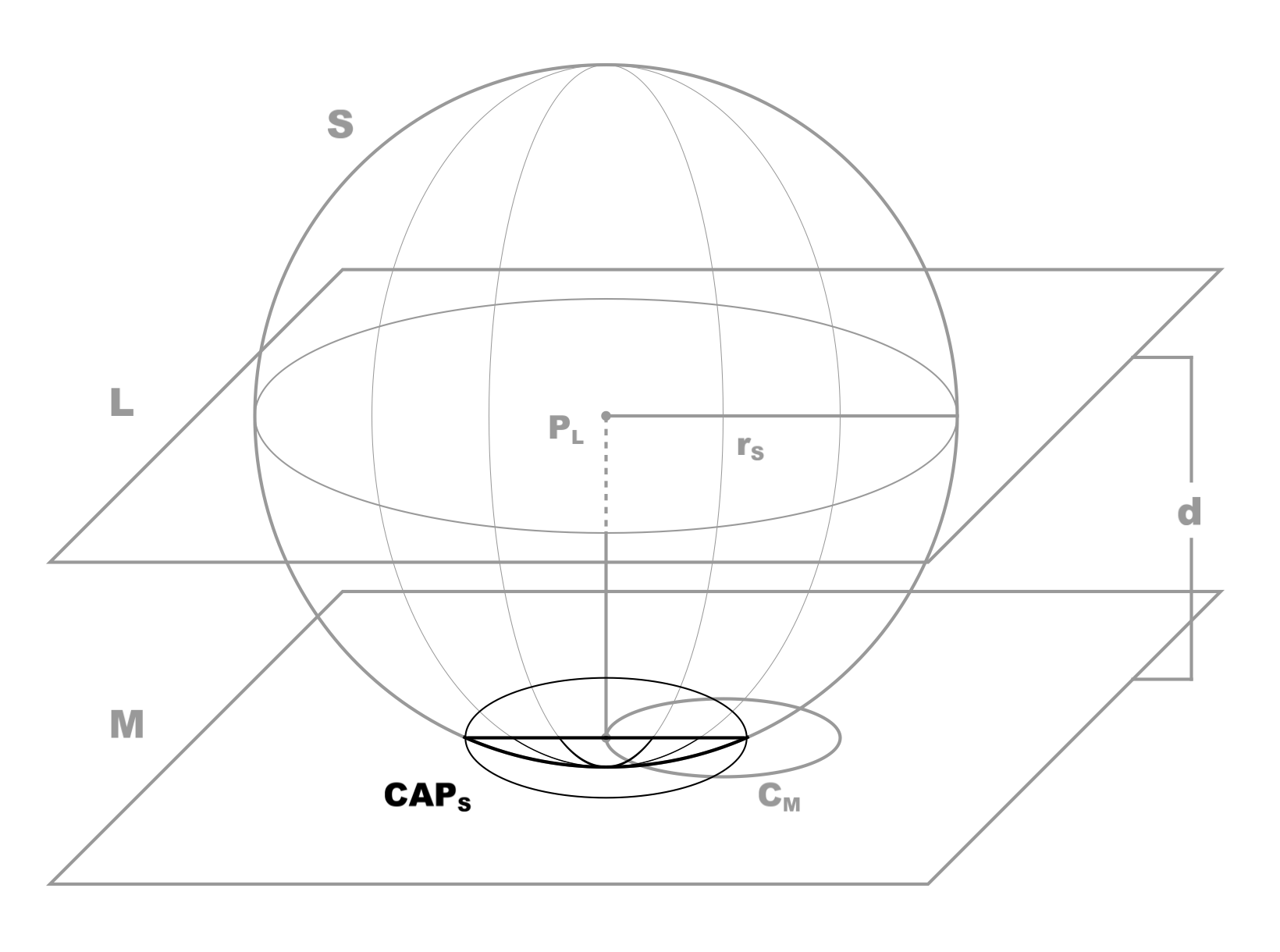
Figure 5. (Click to enlarge.)
Sphere {$S$} at {$t_{M}<t<t_{total\ doom}$}; {$r_{S}>d$}; {$A(\mathit{CAP}_{S})>0$}; {$0<r_{C_{S}}<2r_{C_{M}}$}.
The shape of the intersection of {$S$} with {$M$} is of course a circle, but we are not interested in that. As noted before, the contents of the surface of the expanding sphere (or hypersphere, in the actual model) should “flow” into the Material Plane. Thus what we’re actually interested in is the surface area of {$\mathit{CAP}_{S}$}. We will map that area onto plane {$M$} by drawing a circle {$C_{S}$}, centered at point {$P_{M}$}, with area equal to the surface area {$A(\mathit{CAP}_{S})$} (figure 7).
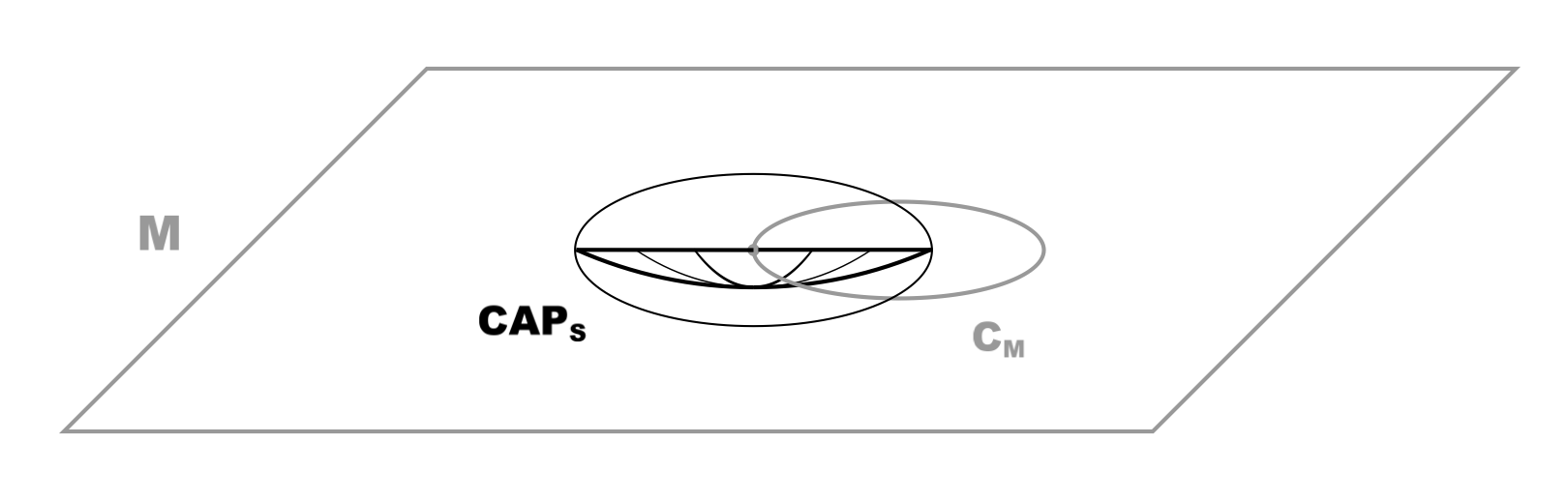
Figure 6. (Click to enlarge.)
{$\mathit{CAP}_{S}$}.
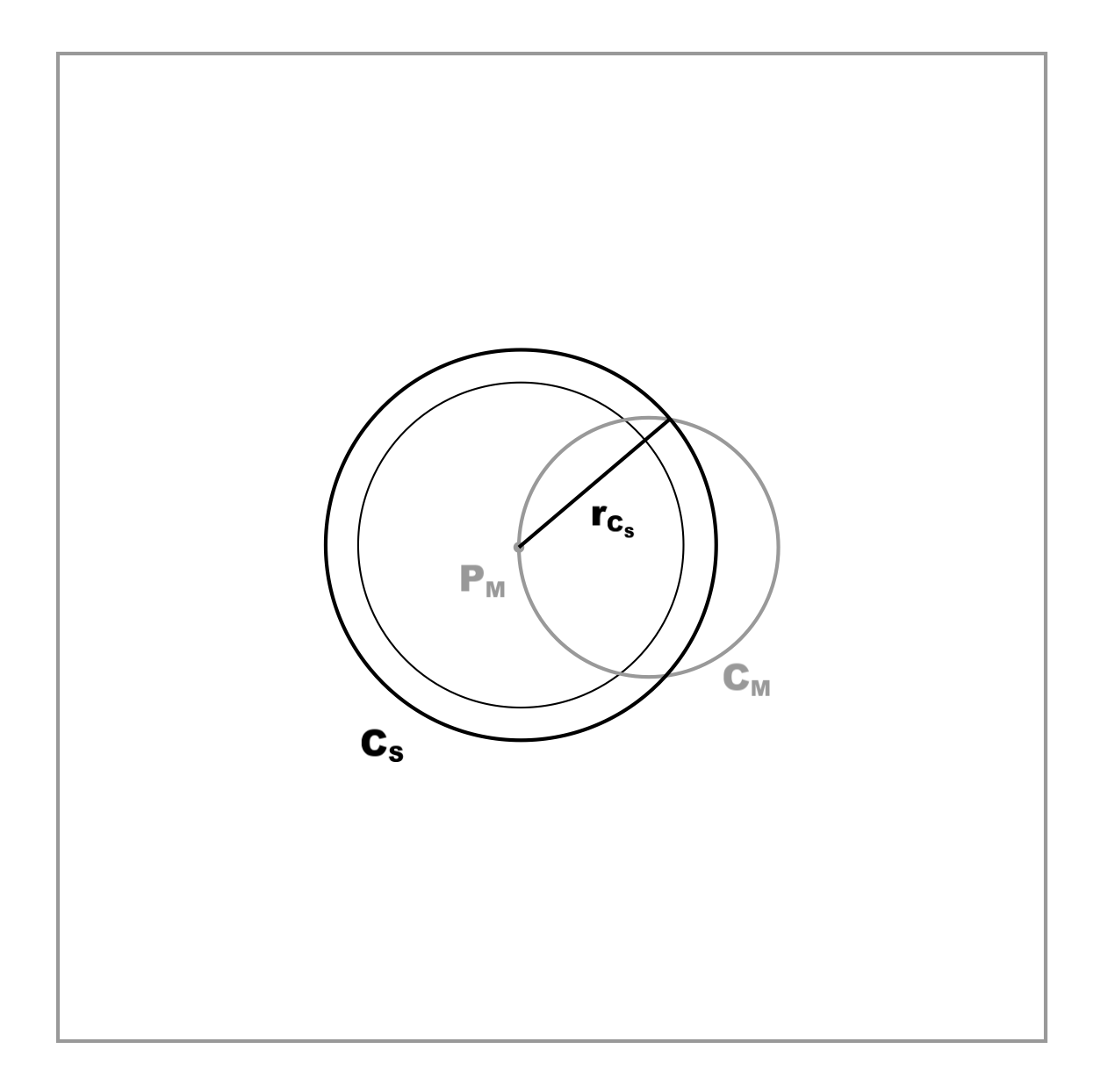
Figure 7. (Click to enlarge.)
Orthogonal view onto plane {$M$}. Note that the smaller of the two circles centered at {$P_{M}$} represents the intersection of {$S$} with {$M$} (i.e., the base of {$\mathit{CAP}_{S}$}), and is not what we are interested in. Rather, we are concerned with {$C_{S}$}, the circle with area equal to {$A(\mathit{CAP}_{S})$}.
As {$t$} increases, {$A(\mathit{CAP}_{S})$}, and thus the area {$A(C_{S})$} of circle {$C_{S}$}, will increase approximately linearly with time as well (after {$t_{M}$}, that is; prior to {$t_{M}$}, {$A(\mathit{CAP}_{S})$} is of course zero); the radius {$r_{C_{S}}$} of {$C_{S}$} will increase approximately as the square root of {$t$}. As {$C_{S}$} grows (remember that it is centered on point {$P_{M}$} on the exterior of {$C_{M}$}), it will encompass an increasingly large sector of the circumference of {$C_{M}$} (figure 8), until a time {$t_{total\ doom}$} is reached when {$C_{S}$} fully contains {$C_{M}$}. (As {$C_{M}$} is our two-dimensional analogue of a planet, its circumference is the one-dimensional analogue of the planet’s surface.)
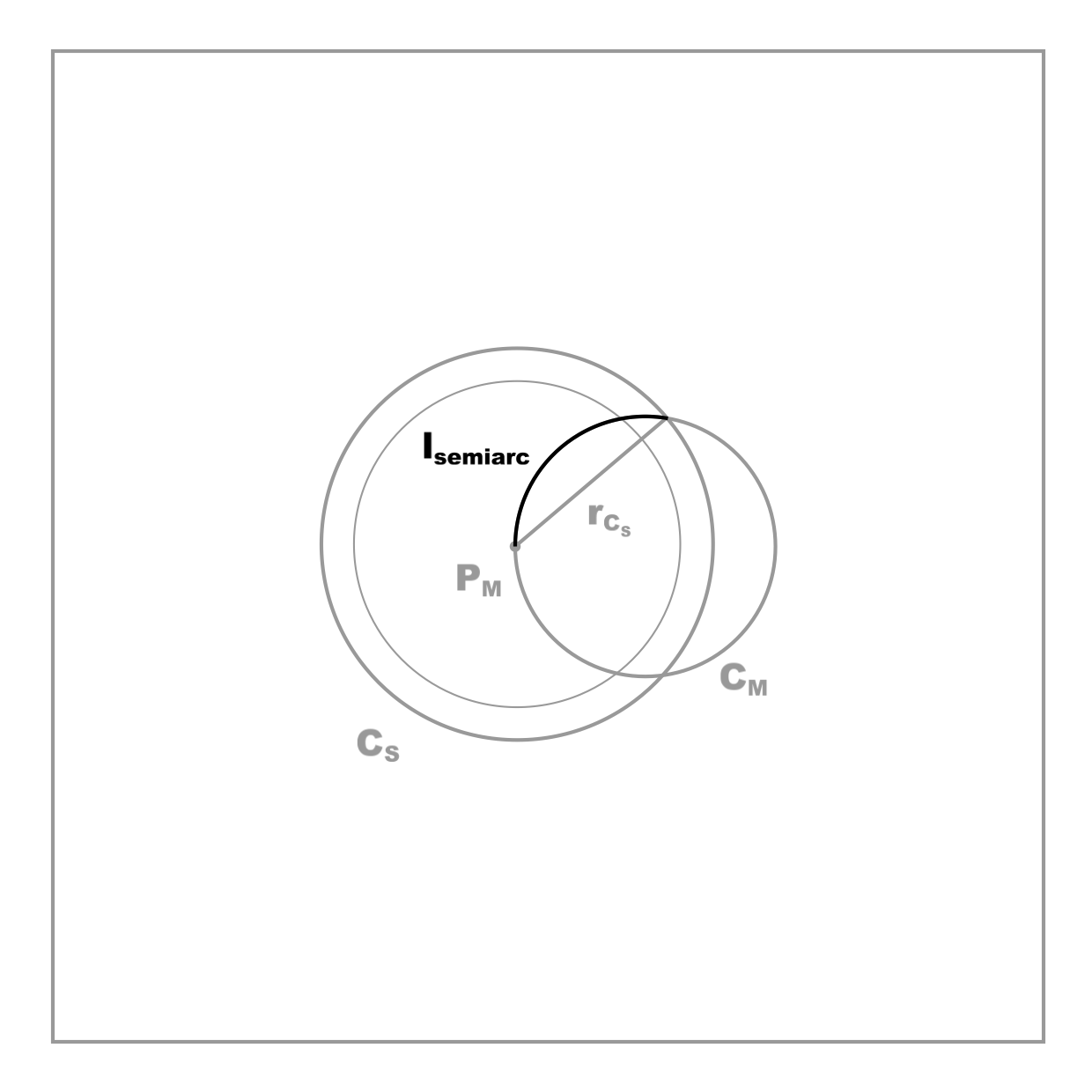
Figure 8. (Click to enlarge.)
One-half of the arc of {$C_{M}$} which is encompassed by {$C_{S}$} is {$l_{semiarc}$}. This is the arc of {$C_{M}$} which is cut off by a chord with one endpoint at {$P_{M}$} and length equal to {$r_{C_{S}}$}.
We can now derive the formula for the arc-length of the encompassed sector of {$C_{M}$}.
Radius of the expanding sphere {$S$}:
{$$ r_{S}=k\sqrt{t} $$}
Surface area of the spherical cap {$\mathit{CAP}_{S}$}:
{$$ A(\mathit{CAP}_{S})=2πr_{S}(r_{S}-d) $$}
(This value, and all subsequent equations that depend on it, will be zero when {$r_{S}\leq d$}, i.e. when {$S$} has not yet grown large enough to intersect {$M$}.)
Radius of circle with area equal to {$A(\mathit{CAP}_{S})$}:
{$$ r_{C_{S}}=\sqrt{\frac{A(\mathit{CAP}_{S})}{2π}} $$}
Arc-length of one-half of the arc of {$C_{M}$} which is contained within {$C_{S}$}:
{$$ l_{semiarc}=2r_{C_{M}}\cdot asin\left(\frac{r_{C_{S}}}{2r_{C_{M}}}\right) $$}
Substituting and simplifying:
{$$ l_{semiarc}=2r_{C_{M}}\cdot asin\left(\frac{\sqrt{k\sqrt{t}(k\sqrt{t}-d)}}{2r_{C_{M}}}\right) $$}
We can see that the value of {$t_{total\ doom}$} (which will occur when {$l_{semiarc}$} equals one-half the circumference of {$C_{M}$}) naturally depends on three variables:
- the planar separation distance {$d$} between {$M$} and {$L$}
- the growth rate coefficient {$k$} of {$r_{S}$} (a constant factor applied to the equation which relates {$r_{S}$} to {$t$})
- the radius {$r_{C_{M}}$} of circle {$C_{M}$} (which is the 2-dimensional analogue of the PCs’ home planet)
So that was the simplified (one-dimension-lower) version. Now we must add one dimension to the above considerations, which, unsurprisingly, makes our task rather more tricky. (There will be fewer diagrams in this part, as I do not have an easy way to depict four-dimensional spaces in a two-dimensional medium.)
We have two parallel three-dimensional spaces, again called {$M$} and {$L$}, separated by a distance of {$d$} in the four-dimensional space within which they’re both embedded; these are the Prime Material Plane, and the city of Lacc in the Plane of Shadow. In {$M$} is a sphere {$S_{M}$} (the world of the player characters). At a point {$P_{M}$} on {$S_{M}$}, we construct a line, perpendicular to space {$M$}; designate the point where this line intersects space {$L$} as {$P_{L}$}. Now we construct a hypersphere (specifically, a 3-sphere) {$H$}, centered at {$P_{L}$}. The radius {$r_{H}$} of hypersphere {$H$} begins at 0 and increases as time passes, the increase going as the cube root of time {$t$} (with a constant growth rate coefficient {$k$}). (This naturally means that the three-dimensional surface area of H will increase linearly with {$t$}.)
At some point {$t_{M}$}, the radius {$r_{H}$} of hypersphere {$H$} will be equal to the distance {$d$} that separates spaces {$M$} and {$L$}. At this time, {$H$} will be tangent to {$M$}. The point of contact will of course be {$P_{M}$} (which, recall again, is a point on the surface of the sphere {$S_{M}$} in space {$M$}). As time continues to pass and {$r_{H}$} keeps increasing, the hypersphere {$H$} will intersect space {$M$}, which will cut off a hyperspherical cap {$\mathit{CAP}_{H}$}.
The shape of the intersection of {$H$} with {$M$} is of course a sphere, but once again that does not interest us; in our scenario, the contents of the three-dimensional surface of the hypersphere should flow into the Material Plane (i.e., space {$M$}). Thus what interests us is the (three-dimensional) surface area of {$\mathit{CAP}_{H}$}. We will map that area onto space {$M$} by drawing a sphere {$S_{H}$}, centered at point {$P_{M}$}, with a volume {$V(S_{H})$} equal to the (3D) surface area {$A(\mathit{CAP}_{H})$}. As {$t$} increases, {$A(\mathit{CAP}_{H})$}, and thus the volume {$V(S_{H})$} of sphere {$S_{H}$}, will increase approximately linearly with time as well (but, again, only after {$t_{M}$}, prior to which {$A(\mathit{CAP}_{H})$} is zero); the radius {$r_{S_{H}}$} of {$S_{H}$} will increase approximately as the cube root of {$t$}. As {$S_{H}$} (which is centered on point {$P_{M}$} on the surface of {$S_{M}$}) grows, it will encompass an increasingly large (circular) sector of the surface of {$S_{M}$}, until a time {$t_{total\ doom}$} is reached when {$S_{H}$} fully contains {$S_{M}$} (i.e., totally encompasses the planet).
So, in order to determine the rate of Lacc’s expansion across the surface of the PCs’ world, we need to determine {$r_{sector}$}, the arc-radius of the circular sector of {$S_{M}$} which is subsumed by {$S_{H}$} at any given time {$t$}. This depends on the radius of the sphere {$S_{H}$}, which we can trivially determine from the volume {$V(S_{H})$}; and that, in turn, is stipulated to be equal to the (three-dimensional) surface area {$A(\mathit{CAP}_{H})$}.
Determining the (3D) surface area of a hyperspherical cap turns out to be a tricky problem, which seems to have been solved in closed form only surprisingly recently. The most recent (and, indeed, only) source I was able to find is a paper called “Concise Formulas for the Area and Volume of a Hyperspherical Cap”, by Shengqiao Li, published in 2011 in the Asian Journal of Mathematics and Statistics. The formula which Li gives for the surface area of a hyperspherical cap makes use of a function called the regularized incomplete beta function:
{$$ A(\mathit{CAP}_{H})=\frac{1}{2}\cdot A(H)\cdot I_{sin^{2}\phi}\left(\frac{n-1}{2},\frac{1}{2}\right) $$}
(Note that {$\phi$} here is one-half the arc angle of {$\mathit{CAP}_{H}$}; this is also known as the colatitude angle.)
As used here, this function takes as its one parameter the number of dimensions {$n$} of the sphere whose surface area is to be computed; in our case this is 3 (remember that a circle is a 1-sphere; a regular sphere, e.g. a planet or a basketball, is a 2-sphere; a hypersphere, i.e. a sphere in four dimensions, is a 3-sphere). Li helpfully gives equivalent forms for this function, for integer {$n\in [1,4]$}. For {$n=3$}, the formula thus becomes:
{$$ A(\mathit{CAP}_{H})=\frac{1}{2}\cdot A(H)\cdot \frac{2\phi-sin(2\phi)}{π} $$}
We can now derive the formula which gives us {$r_{sector}$} (the arc-radius on the planet’s surface of the expanding zone of Lacc’s incursion into the PCs’ world) as a function of {$t$} (time in days).
Radius of the expanding hypersphere {$H$}:
{$$ r_{H}=k\sqrt[3]{t} $$}
Surface area (3D) of {$H$}:
{$$ A(H)=2π^{2}r_{H}^{3} $$}
Colatitude angle of hyperspherical cap {$\mathit{CAP}_{H}$}:
{$$ \phi=acos\left(\frac{d}{r_{H}}\right) $$}
Surface area (3D) of hyperspherical cap {$\mathit{CAP}_{H}$}:
{$$ A(\mathit{CAP}_{H})=\frac{1}{2}\cdot A(H)\cdot (\frac{2\phi-sin(2\phi)}{π}) $$}
Radius of sphere with volume equal to {$A(\mathit{CAP}_{H})$}:
{$$ r_{S_{H}}=\sqrt[3]{\frac{3}{4π}\cdot A(\mathit{CAP}_{H})} $$}
Arc-radius of the circle on the surface of {$S_{M}$} encompassed by {$S_{H}$}:
{$$ r_{sector}=2r_{S_{M}}\cdot asin\left(\frac{r_{S_{H}}}{2r_{S_{M}}}\right) $$}
Substituting and simplifying:
{$$ r_{sector}=2r_{S_{M}}\cdot asin\left(\frac{\sqrt[3]{\frac{4}{3π}\cdot A(\mathit{CAP}_{H})}}{2r_{S_{M}}}\right) $$}
{$$ =2r_{S_{M}}\cdot asin\left(\frac{\sqrt[3]{\frac{2}{3π}\cdot A(H)\cdot (\frac{2\phi-sin(2\phi)}{π})}}{2r_{S_{M}}}\right) $$}
{$$ =2r_{S_{M}}\cdot asin\left(\frac{\sqrt[3]{\frac{2}{3π^2}\cdot A(H)\cdot \left(2\cdot acos\left(\frac{d}{r_{H}}\right)-sin\left(2\cdot acos\left(\frac{d}{r_{H}}\right)\right)\right)}}{2r_{S_{M}}}\right) $$}
{$$ =2r_{S_{M}}\cdot asin\left(\frac{\sqrt[3]{\frac{4}{3}r_{H}^{3}\cdot \left(2\cdot acos\left(\frac{d}{r_{H}}\right)-sin\left(2\cdot acos\left(\frac{d}{r_{H}}\right)\right)\right)}}{2r_{S_{M}}}\right) $$}
{$$ =2r_{S_{M}}\cdot asin\left(\frac{k}{2r_{S_{M}}}\cdot \sqrt[3]{\frac{4}{3}t\cdot \left(2\cdot acos\left(\frac{d}{k\sqrt[3]{t}}\right)-sin\left(2\cdot acos\left(\frac{d}{k\sqrt[3]{t}}\right)\right)\right)}\right) $$}
Once again the value of {$t_{total\ doom}$} (and, more generally, the relationship of the time {$t$} to the radius {$r_{sector}$} of the sector of {$S_{M}$} encompassed by the growing sphere {$S_{H}$} of Lacc’s incursion into the Prime Material Plane) depends on three variables:
- the spatial separation distance {$d$} between {$M$} and {$L$}
- the growth rate coefficient {$k$} of {$r_{H}$}
- the radius {$r_{S_{M}}$} of sphere {$S_{M}$} (i.e., of the PCs’ home planet)
It is customary to assume that the worlds of most D&D settings are approximately Earth-like in basic characteristics, such as size, mass, etc.1 We will therefore set {$r_{S_{M}}$} to match that of Earth: 3959 miles.
That leaves the rate of growth {$k$} and the spatial separation distance {$d$}. These are essentially free variables, in that they are not constrained by any aspect of the model we’ve described so far, nor is there (yet) any obvious reason why either of them should take on any particular value rather than any other. This leaves us free to choose the values of both variables on the basis of adventure design considerations.
As noted previously, we would like to give the PCs a reasonable but not excessive amount of time (namely, somewhere from a week to a month, probably closer to the latter; let’s now make a concrete choice, and name three weeks as our critical time frame) to complete the adventure. Note that this period starts not at {$t=0$}, but rather at {$t=t_{M}$}, i.e. the time at which the hypersphere radius {$r_{H}$} is just large enough for the hypersphere {$H$} to make contact with space {$M$} (the Prime Material Plane). Likewise, the end of the critical period (i.e., the time at which, if the PCs have not defeated Tenaris Xin, they fail in their quest and their world is forfeit) occurs not at {$t=t_{total\ doom}$} (the hypothetical—and, as it turns out, irrelevant—time at which the sphere {$S_{H}$} would encompass the entirety of {$S_{M}$}); rather, it’s the moment at which Xin completes his ritual (whereupon the PCs’ world is absorbed into Lacc immediately).
Obviously, we may stipulate Xin’s ritual to take however long we wish it to take. If we say it takes three weeks to complete, then that’s how long it takes. The task is to make the ritual’s casting time (and, ideally, every other detail of the adventure setup) seem to be non-arbitrary.2 There’s also another, related, design goal: to communicate to the players (i.e., to give their characters a way to intuit) that they are facing a concrete deadline (and what the time scale of that deadline is).
Here is how we will do it. In “Gates of Oblivion”, the means by which Lacc consumes a world is linked to three magical gates (the Colorless Gate, the Empty Gate, and the Hollow Gate); these are arranged in an equilateral triangle (figure 9), with Tenaris Xin’s tower at the center, equidistant from all three. Each Gate is exactly 16 miles from Xin’s tower. (This results in a triangle with sides approximately 27.7 miles long.)
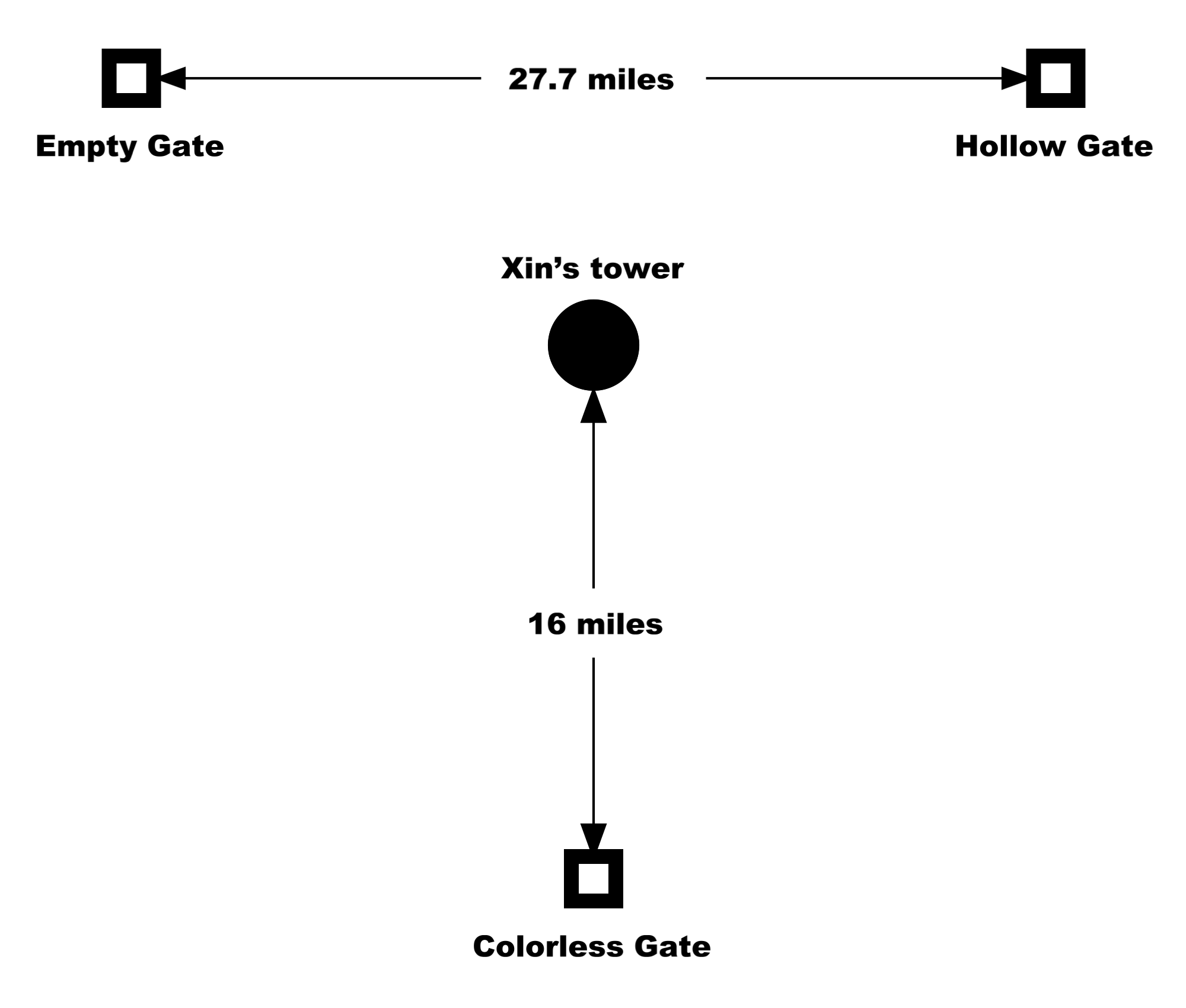
Figure 9. (Click to enlarge.)
The three magical Gates and the tower of Tenaris Xin, in Lacc, the City of Monoliths.
We are now going to slightly modify the setup described above. Instead of a single point {$P_{M}$} on the planet’s surface, we identify three points, arranged in an equilateral triangle, 27.7 miles to the side. From each of these points, we will construct a line perpendicular to {$M$}, then a hypersphere with center at the point where the line intersects {$L$}, etc., all as described previously. Thus we will have not one but three expanding zones of darkness (figure 10), as Lacc will make contact with the world of the PCs at three points (the vertices of the triangle).
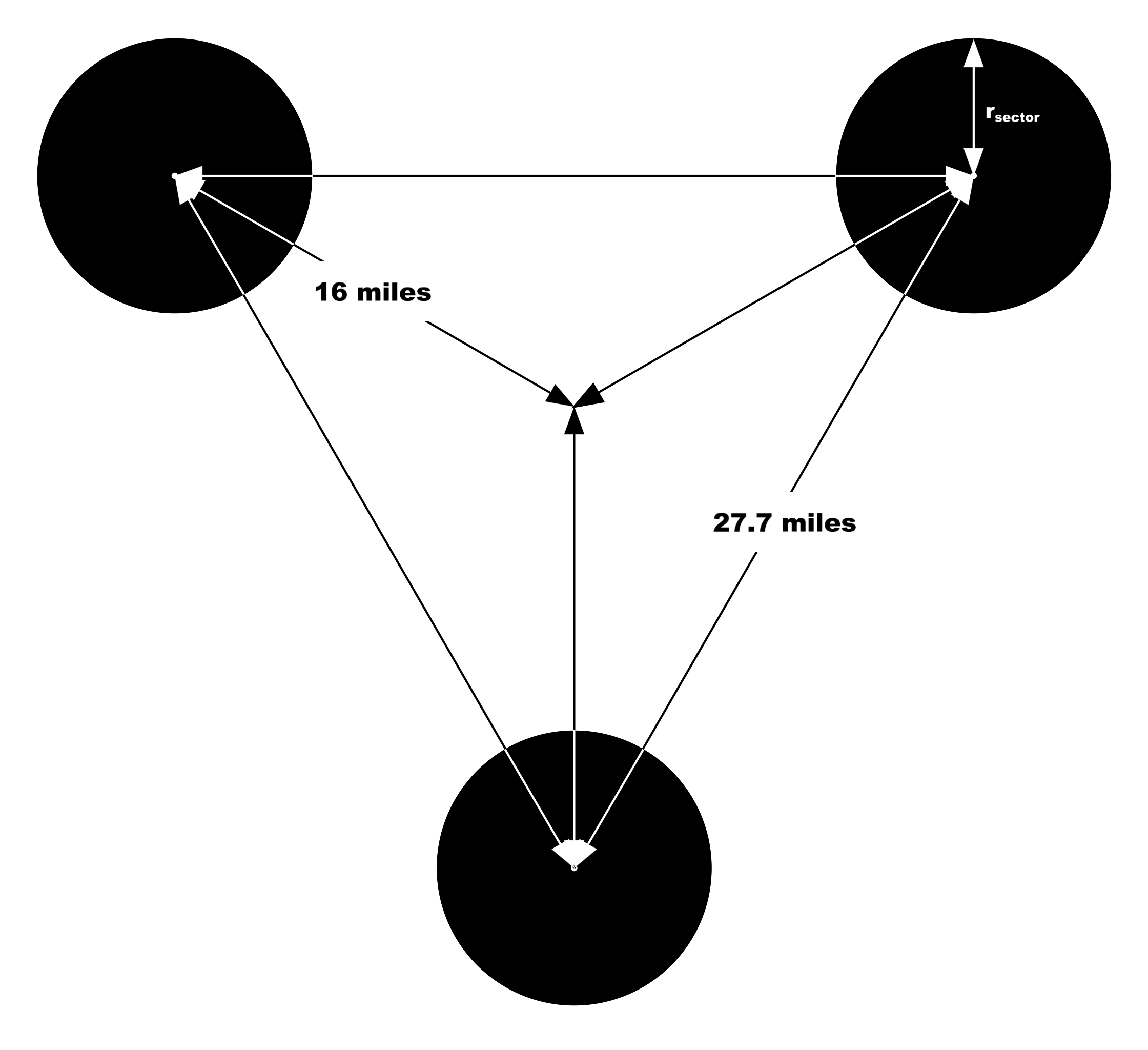
Figure 10. (Click to enlarge.)
Not one, but three distinct intrusion zones, located somewhere on the surface of the player characters’ home world.
Furthermore, we will now specify the spatial separation distance {$d$} to be 16 miles (matching the distance from each of the three Gates to the tower of Tenaris Xin).
This has several results. First, it naturally creates a temporal Schelling point which the players can identify as a plausible candidate for when something might happen: namely, the moment when the three expanding zones meet (figure 11).3 (It does not take a great leap of intuition to suspect that this will be a bad thing.) This is the hint to the players (and the PCs) that there’s a much closer deadline than merely “when the intrusion zone expands to encompass the whole world” (which will quite clearly be many months or even years away, given the observed expansion rate of the intrusion zones).

Figure 11. (Click to enlarge.)
The expansion of the three intrusion zones brings them into contact at {$t=t_{zone\ contact}$}, when {$r_{sector}$} is equal to one-half the distance between the centers of the three zones (and also, necessarily, one-half the distance between the three Gates in Lacc).
Second, it allows the players to identify parallels between elements of the setup, which both creates the perception of a logically connected system and offers hints that point the PCs to the key locations which they must visit in order to gain more information about Tenaris Xin’s plans and, thereby, to successfully complete the adventure. That is: the center points of the intrusion zones form a triangle 16 miles from a center point. The spatial separation distance (which the PCs will have to cross in their journey to the heart of Lacc; see below) is likewise 16 miles; noticing this will give the PCs a hint that this value is somehow important. When the PCs arrive in the Plane of Shadow, they can notice the correspondence of the location of one of the Gates to the center point of the intrusion zone in their world, and intuit that the two other Gates exist and that they are important. If they think to travel to the center point of the triangle formed by the three Gates (which again is 16 miles away from each Gate), they will arrive at Xin’s tower.4
(Needless to say, none of these hints or deductions should be the only avenue by which the players can reach any of the aforementioned conclusions or learn any of the information I’ve described. In accordance with the three clue rule, there should be multiple hints or clues pointing the players toward these nodes in the scenario structure. Enumerating the rest of that scenario structure is beyond the scope of this post. Here it is important to notice only that carefully planning out the geometry of Lacc’s incursion allows us to use that very geometry as one source of clues for the players. This rewards players who pay attention to such details, encourages careful thought, and contributes greatly to the sense of the adventure’s events as coherent, logical, predictable, and amenable to understanding.)
Having specified the planetary radius {$r_{S_{M}}$} and the spatial separation distance {$d$}, it now remains for us only to pick the growth rate coefficient {$k$}. We will select a value of {$k$} that results in a period of exactly three weeks between {$t_{M}$} (the time at which the three hyperspheres of Lacc’s intrusion zones first make contact with the Prime Material Plane, and the beginning of the adventure) and {$t_{zone\ contact}$}3 (the time when the three expanding intrusion zones on the surface of the PCs’ world meet at three points of tangency), which we have decided is the moment at which Tenaris Xin completes his ritual, and the PCs’ world is permanently absorbed into the City of Monoliths. This value is 5.36.5
The formula we previously derived for the arc-radius of each of the three intrusion zones is:
{$$ r_{sector}=2r_{S_{M}}\cdot asin\left(\frac{k}{2r_{S_{M}}}\cdot \sqrt[3]{\frac{4}{3}t\cdot \left(2\cdot acos\left(\frac{d}{k\sqrt[3]{t}}\right)-sin\left(2\cdot acos\left(\frac{d}{k\sqrt[3]{t}}\right)\right)\right)}\right) $$}
And the values we’ve chosen for our three key variables are:
- {$r_{S_{M}}$} (the radius of sphere {$S_{M}$}, the PCs’ home planet): 3959 miles
- {$d$} (the spatial separation distance between {$M$} and {$L$}): 16 miles
- {$k$} (the growth rate coefficient of the hypersphere radii {$r_{H}$}): 5.36
Substituting those values, we get:
{$$ r_{sector}=7918\cdot asin\left(\frac{5.36}{7918}\cdot \sqrt[3]{\frac{4}{3}t\cdot \left(2\cdot acos\left(\frac{16}{5.36\cdot \sqrt[3]{t}}\right)-sin\left(2\cdot acos\left(\frac{16}{5.36\cdot \sqrt[3]{t}}\right)\right)\right)}\right) $$}
And the resulting values of {$r_{sector}$}:
| Day | {$r_{sector}$} |
|---|---|
| 0–26 | 0 |
| 27 | 1.9 |
| 28 | 3.6 |
| 29 | 4.7 |
| 30 | 5.6 |
| 31 | 6.4 |
| 32 | 7.1 |
| 33 | 7.7 |
| 34 | 8.3 |
| 35 | 8.8 |
| 36 | 9.3 |
| 37 | 9.8 |
| 38 | 10.3 |
| 39 | 10.7 |
| 40 | 11.1 |
| 41 | 11.5 |
| 42 | 11.9 |
| 43 | 12.3 |
| 44 | 12.6 |
| 45 | 13.0 |
| 46 | 13.3 |
| 47 | 13.7 |
| 48 | 14.0 |
| 49 | 14.3 |
| 50 | 14.6 |
| 51 | 14.9 |
| 52 | 15.2 |
| 53 | 15.5 |
| 54 | 15.7 |
| 55 | 16.0 |
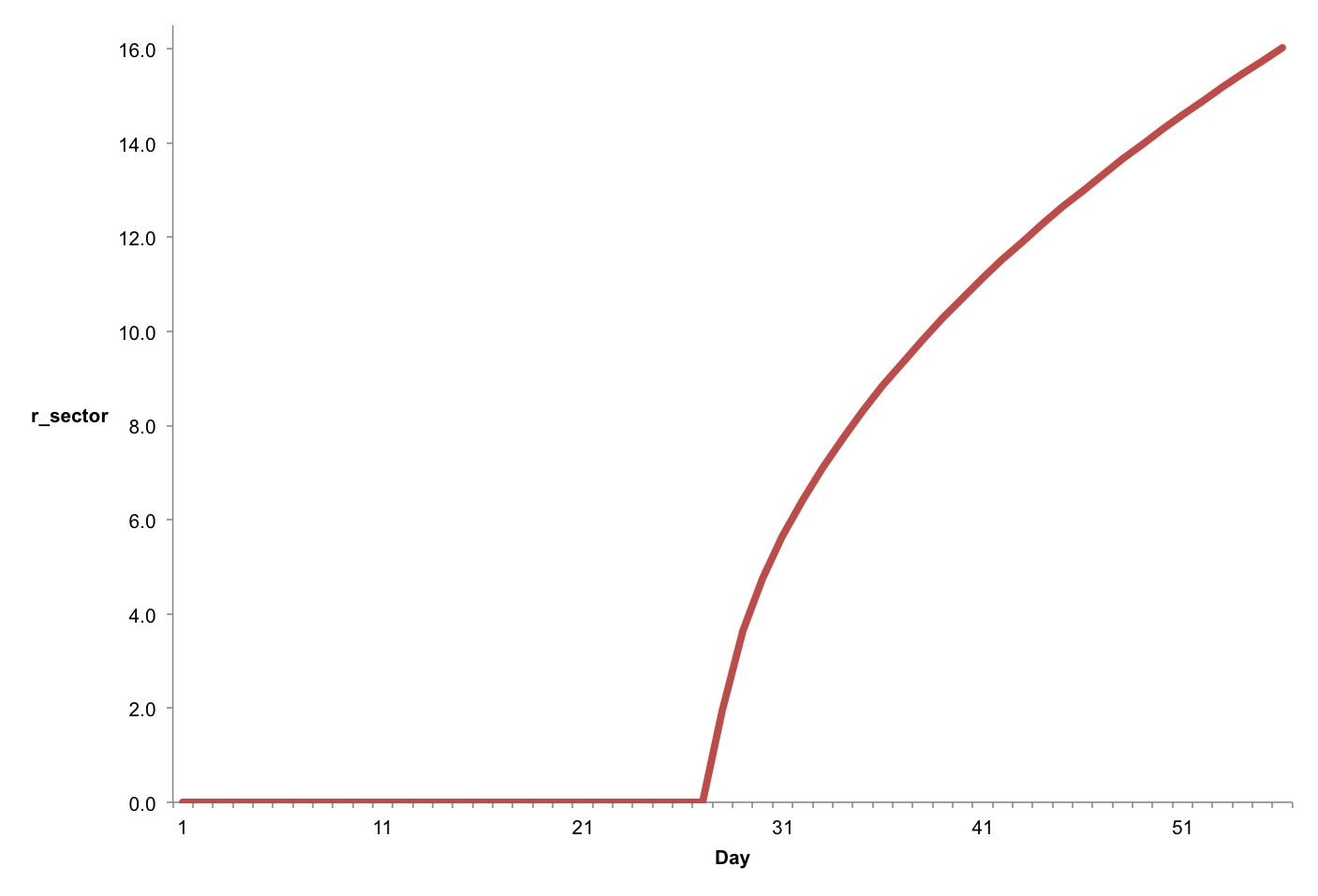
Figure 13. (Click to enlarge.)
Lacc intrusion zone radius in miles as a function of time in days since Tenaris Xin begins his ritual.
Rows in bold are key days. Day 27 is {$t_{M}$}, when Lacc first makes contact with the PCs’ home world, and the three intrusion zones appear (27.7 miles apart from one another) somewhere on the world’s surface (growing to a radius of 1.9 miles within that first day). Day 48 is {$t_{zone\ contact}$}, when the three intrusion zones first touch one another, and begin to merge; this is the first of the two possible endpoints for the adventure. Day 55 is {$t_{zone\ merge}$}, at which point no gap remains between the three intrusion zones; this is the second possible endpoint for the adventure. (The DM may select one of the endpoint dates in advance, or hold off the decision until later in the adventure; needless to say, in the latter case, he should be careful not to provide any hints which identify one of the dates as the endpoint.)
By the way, what are we to make of the period prior to day 27? (This is the period when the hyperspheres {$H$} are expanding but have not yet reached {$M$}, the Prime Material Plane; so there are as yet no intrusion zones on the surface of the PCs’ world, i.e. {$r_{sector}$} is zero.) We may suppose that after selecting a world for assimilation into Lacc, Tenaris Xin begins an almost-month-long process of magical preparation, during which time the City of Monoliths begins “reaching” across the interplanar distances toward the Prime Material World of the player characters. It is reasonable to assume that there is no feasible way for the PCs (or anyone else on their world) to know about this process prior to {$t_{M}$} (day 27). However, if the DM wishes to give the players a hint of what’s to come (e.g. if using this adventure in a larger campaign), he may have signs and portents manifest during this time period (visions experienced by oracles, for example, or warnings from the gods, or strange observations recorded by scholars of the arcane who study the lore of the planes, or other things of this nature).
(Incidentally, what would be the value of {$t_{total\ doom}$} given the values we’ve selected for our key variables? That is, how long would it take for Lacc to fully engulf the PCs’ home world in the absence of the ritual (i.e. if the hyperdimensional model described above were applied to the adventure as written)? We are looking for the lowest value of {$t$} that yields an {$r_{sector}$} equal to or greater than one-half the circumference of {$S_{M}$} (that being {$πr_{S_{M}}$}, i.e. ~12,437.6 miles). This value happens to be 772,797,939 days, or approximately 2,117,254 years.)
Finally, do we now have a non-arbitrary answer for where on the surface of the PCs’ world Lacc’s intrusion zones should be located? Yes: from Tenaris Xin’s perspective, Lacc should always make contact with a target planet in some location as remote as possible from civilization, to minimize the chance that any powerful inhabitants of that world (i.e., high-level characters such as the PCs, and/or any other entities likely to possess the capability to stop Xin’s plans) will discover the intrusion zones in time to learn their nature, reach Xin’s tower, and interrupt his ritual. (Determining what other measures Xin might take to minimize the chance of being discovered and interrupted in time, as well as the details of how the PCs will, despite Xin’s plans, learn of Lacc’s incursion before it’s too late—as indeed they must, or else the adventure can’t take place—is left as an exercise for the DM.)
1 See, e.g., Concordance of Arcane Space from the Spelljammer boxed set, which places Oerth, Krynn, Toril, etc. in the same celestial body size category, drawing no distinctions between them. Exceptions do exist, such as Mystara (the planet on which the “Known World” campaign setting of D&D Basic is located), which features a significantly smaller size and hollow interior. (Of course, players in the Known World may never even realize the existence of these major structural differences, due to the “world shield”—an internal layer of ultra-dense material; perhaps neutronium?—that, among its other effects, provides sufficient mass to bring Mystara up to Earth-normal gravity.) ⇑
2 “Seem” is really the key word here. This is not an idea original to me (I recall first seeing the formulation I give here in a social media post which I have long since lost the link to), but: when creating explanations for whatever the player characters encounter, you only need to go two levels deep. That is, if the players ask why something is the way that it is, they should be able to discover an explanation; and if they ask why that is the way that it is, they should be able to discover an explanation for that, too; and at that point, they will not keep asking, because you will have successfully created the impression that there’s an explanation for everything. Furthermore, if you then, e.g., tie the explanation for the third thing back to the first thing, you have created a complete system which can support explanations of arbitrary depth.
(One can, of course, always ask “but why is this whole system the way that it is”, but given that the same question can be asked just as easily of the real world, it’s unlikely that the lack of an in-world answer will detract from verisimilitude and immersion. If the players do, after all, ask the question, Morgenbesser’s reply should suffice.) ⇑
3 Actually, if the players consider the matter carefully, they will realize that there are two uniquely identifiable moments here. One—call it {$t_{zone\ contact}$} (figure 11)—is the moment when the three expanding zones come into contact, i.e. the moment at which the three subsumed circular sectors of the planet’s surface are tangent to each other. This will occur when the arc-radii of the subsumed surface sectors are equal to one-half the length of the sides of the equilateral triangle formed by the points of contact, i.e. ~13.86 miles. The other—call it {$t_{zone\ merge}$} (figure 12)—is the moment when there is no longer any gap in the middle of the three zones; this will occur when the arc-radii of the subsumed surface sectors are equal to the distance of a vertex of the triangle from the triangle’s center point, i.e. 16 miles.
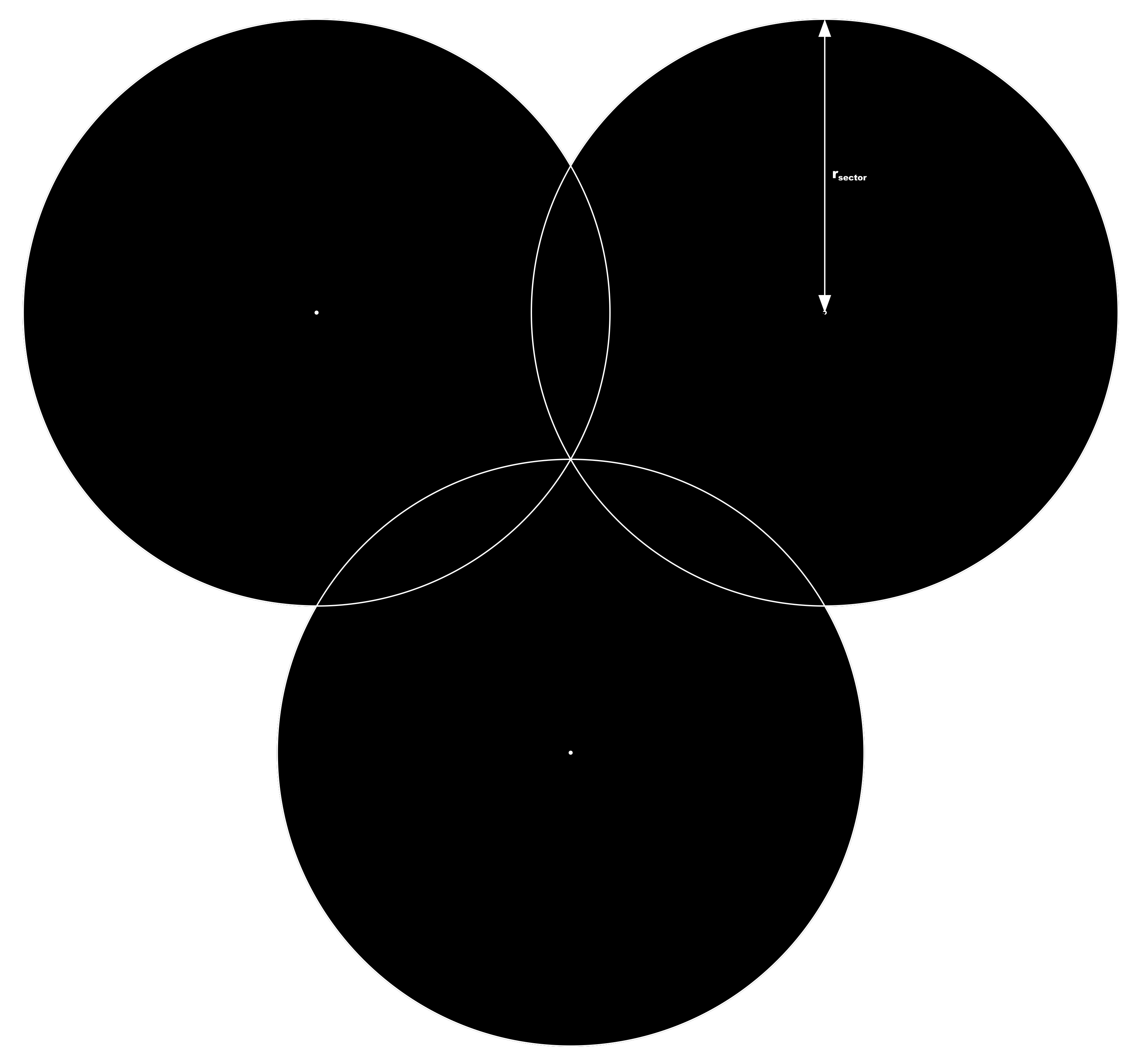
Figure 12. (Click to enlarge.)
The three intrusion zones expand far enough to fully merge (leaving no gap in the middle between them) at {$t=t_{zone\ merge}$}, when {$r_{sector}$} is equal to the distance from the center of each zone to the center of the triangle (which is, necessarily, also the distance from each of the Gates to Xin’s tower).
These two moments will—given the values we’ll choose for our key variables—occur one week apart. From a design standpoint, this works in our favor, as the ambiguity in which of these two key moments marks the completion of Tenaris Xin’s ritual offers the DM a means of either giving the PCs an extra week of time to succeed in their quest (if they’ve made slow progress), or not (if they’ve made good time). ⇑
4 And—strictly as a bonus for very clever players—if they manage to deduce the hyperdimensional structure of Lacc’s incursion, the players can work out the way in which the expansion rate of the three intrusion zones depends on the geometric layout of the Gates, the tower, and the spatial separation distance between the two planes of existence. The success of the PCs should in no way depend on making this leap; it exists only as a reward for players who wish to unravel the puzzle, to reinforce the sense of underlying order and logical coherence which is created by the existence of the mystery in the first place. ⇑
5 Unlike the spatial separation distance, there is no need to justify the growth rate coefficient in any “in-universe” way. It’s well known that our own universe is full of such essentially arbitrary constants, which have the values that they have for no reason other than “that’s just the way it happens to be”. One may appeal to anthropic reasoning to justify some such values, but philosophical points like this are epiphenomenal with respect to our design considerations here.
Of course, another option is to stipulate that this value is not some universal constant but rather a variable, which may depend on any number of factors, from the mystical to the logistical. Perhaps Lacc’s intrusion zones expand faster on worlds where a greater portion of the mortal population are sinners or evildoers, making {$k$} a sort of (inverse) measure of a world’s aggregate righteousness. Or perhaps the Gates, and Lacc’s expansion, must be powered by the souls of the damned, which Xin sources from fiendish contacts in the Lower Planes, exposing Lacc’s incursion timeline to supply-chain disruptions caused by current events in the Blood War. One may derive an endless variety of plot hooks from such free variables. ⇑

Recent Comments