Extreme D&D DIY: adventures in hypergeometry, procedural generation, and software development (part 2)

In part 1, we developed a mathematical model to determine the timeline of key events in a modified version of the D&D adventure “Gates of Oblivion”, in which the player characters must repel an incursion into their home world by Lacc, the vast, shadowy City of Monoliths. This time, we’ll examine another key part of running that adventure: the maps.

The need for maps

As I noted last time, every aspect of a well-designed adventure should contribute to the adventure’s feel. In the case of “Gates of Oblivion”, the players should have a strong experience of Lacc as impossibly vast, maybe even infinite; the broad avenues (silent except for the grinding sound of great masses of stone and the distant moans of the unquiet dead) and the great monoliths of black stone should seem to stretch endlessly in all directions. From the text of the module:

The sky overhead is a featureless black, and ebon monoliths loom on all sides, divided by broad avenues. The avenues are layered with bones, many of them humanoid, though the bones of dragons and other monstrous beasts are visible as well. Some of the monoliths flicker with ghostly radiance, which does little to illuminate the darkened expanse. The blackened vault of heaven seethes with scraps of shadow, and the bone-strewn avenues are choked with tenebrous shapes that flit about without direction and purpose. In some places, vast mounds of rubble or dunes of pale sand obscure the bones of the avenue.

Lacc is a haunting and ever-shifting environment. Strings of glowing runes dance across the surfaces of the monoliths, while half-seen shapes twist and flutter across the featureless sky. Pools of sludgy black water gather inside the skulls of giant beasts, and the breeze carries the laments of countless tortured souls. Still, despite the shadows that flit through its streets, most of Lacc is desolate and empty. Though it is not truly infinite, a man would die of old age before he could cross the city on foot.

Very atmospheric!

But there’s a problem. While the module does include several combat maps (one for the interior of Xin’s tower, and one each for the immediate vicinity of the three magical Gates), they are tiny, describing, in total, less than half a square mile of area. Meanwhile, we are given a well-stocked random encounter table for Lacc, and a solid chunk of the adventure consists of traveling through the city, encountering various things, people, and creatures (many of which encounters are likely to resolve via combat).

Of course, these encounters may be resolved in the “theater of the mind” style, with the DM simply describing the environment, positioning, distances, etc.; but, for one thing, that is distinctly less fun for any players who enjoy tactical combat challenges (and if your players do not, then it’s not entirely clear why you’re running an 18th-level D&D 3.5 adventure), and for another thing, using “theater of the mind” style for encounters that take place in a strange, alien environment (as opposed to something like “a forest road”) can create a feeling of unreality and dissociation from the game world, which severely detracts from the play experience.

In many other cases similar to this one, DM might find it easy enough to quickly sketch a map of a very small section of a very large, abstractly specified environment (whether that’s a city or an extensive cavern system or whatever else), just big enough for a combat encounter… but, for one thing, that is unusually tricky in this case due to the sizes and distances involved (see below); and for another thing, being able to see the edges of the map creates a claustrophobic feeling for the players (“I want to move 100 feet that way” “Uh… that’s off the map, so…” “Eh, never mind, I’ll just… kinda… stay in this area…”), which is precisely the opposite of what we want here. (Of course the DM can improvise the off-the-map areas, but then that just makes things feel unreal again: if the DM is making the place up as he goes along, that’s pretty much the same thing as the place not really existing in any meaningful sense.)

What to do? Well, recall what we know: Lacc is vast, most of it is empty, and it’s filled with endless miles upon miles of basically the same sort of thing: bone-strewn avenues and black monoliths. Here, by the way, is what we are told about the dimensions of both of those things:

The avenues of Lacc range from 50 to 400 feet wide. Any street narrower than 100 feet wide is invariably rough terrain, as mounds of rubble and heaps of bones make progress difficult. A typical monolith is a block of black stone 200 feet wide, 200 feet long, and 600 feet tall, with a pyramidal crest (though they come in all shapes and sizes).

This is a setup that practically screams “procedural generation”.

With a simple generator, we can create, in advance, multiple (arbitrarily many, in fact) very large maps of big (i.e., a dozen miles or more across) chunks of Lacc. At any point in the adventure when the PCs are traveling through the city and encounter something interesting (i.e., something with which the encounter is worth playing out, rather than merely describing), the DM can pick a spot somewhere in the middle of one of these maps and set the encounter there. The players will then find that their characters can move even large distances in any direction, and not find themselves “off the map”—in other words, the players will feel like the characters’ surroundings really exist, can be described concretely, aren’t just being made up on the spot, etc. This sort of thing will go a very long way toward making Lacc feel like a real place. And that will, in turn, contribute to making the city feel like (ironically) a fantastic place—eerie, alien, haunting.

There’s also another major advantage of having large combat maps (i.e., that cover a large area and can support tactical-scale movement across substantial distances): it broadens the tactical scope of combat by enabling a wider variety of movement and positioning options, long-range attacks, etc. to be used in play. (Consider, for example, how rare it is to find a tactical-scale map that covers an area large enough that it is possible for two opponents to be placed on the map in such a way that they are too far apart to hit each other with a fireball. 600 feet is just 120 grid squares on a standard 5-foot-square grid, but even that evidently turns out to be too much—when did you last see a combat map that was more than 120 grid squares across?¹)

(Note that what we’re mapping here is a straightforwardly two-dimensional street layout. The hypergeometry described in the previous post is not relevant here; it’s not Lacc’s incursion into the Prime Material Plane that we’re concerned with, this time, but the landscape of the city itself, once the player characters make their way into it; and—locally, at least—Lacc will be experienced by the PCs as having the same sort of basic geometry as any other city. Of course, the DM is free to create various weird effects and consequences of Lacc’s alien nature, which may be linked to the hyperdimensionality we previously discussed—but that is beyond the scope of this post.)

Our procgen should be very simple. It should generate a layout of streets and monoliths—nothing else. (If the DM wishes to place specific things in some spots of the map, that is trivial to do, even on the fly; it’s generating the basic layout that’s the tedious and not-doable-spontaneously part, so that’s what we’re focusing on.)

Must we DIY?

Before we proceed, a seemingly reasonable question might be: why should I need to write a custom procgen for this? Surely there are innumerable D&D map generators out there already? Indeed there are, but I have been able to find none which can do, or can easily be configured to do, something that is both so simple and so specific. (This, I find, is a pattern which recurs often, whenever one determines to really do something the right way, and refuses to accept compromises for the sake of convenience.)

Let’s look at a couple of examples:

• City Generator by ProbableTrain
  • Ludicrously complex and nigh-impenetrable controls. In any case, as far as I can tell, no way to make the simple but specific sort of map I want. (Maybe I’m wrong about that, but with a UI this hard to understand, how would I know?)
• Medieval City Generator by watabou
  • Not even close. No configuration, highly opinionated city and map design.
• Fantasy Town Generator
  • Basically the same problem as the previous one.
• Random City Map Generator
  • Same problem.
• Fantasy Town Generator by donjon
  • Same problem.

None of these are even approximately what we need here. None can be configured to output a simple rectilinear grid, with arbitrary (and quite large) dimensions, consisting of streets of a certain range of widths with rectangular buildings of a certain range of sizes. It’s such a simple thing, and yet—none of these city map generators have anything even sort of like this capability. They’re just not designed to do what we want, which, again, is both extremely simple (all the graphical “frills”, all the ornamentation, all the styling details offered by all of the above generators—it is all absolutely worthless for our purposes) and very specific (any deviation whatsoever from the requirements makes the results useless, because Lacc is not a generic vaguely-medieval city with some houses and castles and such—it is the City of Monoliths, and not anything else).

There’s nothing for it: we have to write our own.

In the next section, I’ll talk about the reasoning behind the algorithm we’ll use. Afterwards, I’ll give a high-level explanation of the algorithm, and comment on some design decisions. (There’s a link to the complete code at the end of the post.)

Developing the algorithm

First, we should define some key parameters. One pair of key parameters is the permissible range of dimensions for the footprint of monoliths. (That is, we care about their width and length, not their height; of course we can also generate random height values if we wish, but since the height of a monolith does not in any way affect the heights of neighboring monoliths, no special algorithm is needed for this. We may return to this point later.)

The module text quoted above informed us that a typical monolith is “200 feet wide, 200 feet long … (though they come in all shapes and sizes)”. Let us now pick a reasonable range—say, that length and width should vary, independently and uniformly, from 150 feet to 600 feet, in 50-foot increments. (As we’ll see shortly, the 50-foot increment of variation will permit us to represent the map in a very efficient way.) We can alter the values of these parameters later, of course.

The other key parameter is the permissible set of possible street widths. This is also given in the module text: “The avenues of Lacc range from 50 to 400 feet wide.”. (We will once again assume that street widths vary in 50-foot increments.) However, for the first iteration of our algorithm, we will actually ignore this variability, and only include 50-foot-wide streets. (We will relax this restriction later, of course.)

We are ready to proceed.

Divide & conquer

One obvious approach might be the following:

1. Start with one available lot (i.e., rectangular region of map not divided by any streets running through it), spanning the whole map.
2. Grab a lot from the set of available lots.
   • If that lot is already no greater, in both dimensions, than the maximum size of a monolith (i.e., if both the lot’s length and its width are within the permissible ranges for those parameters), set it aside as claimed.
   • Otherwise, divide the lot by placing a street such that the lot is cut along its shorter axis (i.e., we want to divide a long and narrow lot into two lots of a more equitable aspect ratio, rather than dividing it into two equally long but even narrower lots).
     • Place this dividing street not necessarily equidistantly from the two ends of the lot, but at a uniformly-randomly selected position, picked in 50-foot increments from the permissible positions, which are only those positions that result in the two lots resulting from the division both being no smaller than the minimum permissible monolith size. (In other words, we do not want to end up with any lots that are too small to fit a monolith.)
     • The ends of the street should not extend beyond the boundaries of the lot.
   • For each of the two lots created by the division, if the lot is already the appropriate size (by the same criteria as above), set it aside as claimed. Otherwise, place it back into the set of available lots.
3. If there are still lots available, repeated step 2.
4. All lots should now be claimed. Place a monolith on each.
5. Done!

The code (leaving out assorted boilerplate, utility functions, etc.) is below. (Note that the distance measurements are in units of 50-foot increments, i.e. a lot width of 3 represents a lot 150 feet wide, etc. This convenient uniformity is the advantage of enforcing 50-foot increments in variation of key proportions.)

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12
};

L.lots = [ { x:      0,
			 y:      0,
			 width:  L.gridWidth,
			 height: L.gridHeight
			 } ];
L.claimedLots = [ ];

function newStreetDividingBoundingBlock(block) {
	let streetWidth = 1;
	if (block.width > block.height) {
		return {
			width:  streetWidth,
			length: block.height,
			orientation: "v",
			x: (  block.x 
				+ L.minMonolithFootprint 
				+ rollDie(block.width - 2 * L.minMonolithFootprint - streetWidth)),
			y: block.y
		};
	} else {
		return {
			width:  streetWidth,
			length: block.width,
			orientation: "h",
			x: block.x,
			y: (  block.y 
				+ L.minMonolithFootprint 
				+ rollDie(block.height - 2 * L.minMonolithFootprint - streetWidth))
		};
	}
}

function lotIsClaimable(lot) {
	return (   lot.width  <= L.maxMonolithFootprint
			&& lot.height <= L.maxMonolithFootprint);
}

function newLotsAfterStreetDividesLot(street, lot) {
	if (street.orientation == "h") {
		let topLot = {
			x:      lot.x,
			y:      lot.y,
			width:  lot.width,
			height: street.y - lot.y
		};
		let bottomLot = {
			x:      lot.x,
			y:      street.y + street.width,
			width:  lot.width,
			height: lot.y + lot.height - (street.y + street.width)
		};

		return [ topLot, bottomLot ];
	} else {
		let leftLot = {
			x:      lot.x,
			y:      lot.y,
			width:  street.x - lot.x,
			height: lot.height
		};
		let rightLot = {
			x:      street.x + street.width,
			y:      lot.y,
			width:  lot.x + lot.width - (street.x + street.width),
			height: lot.height
		};

		return [ leftLot, rightLot ];
	}
}

function subdivideLots() {
	while (L.lots.length > 0) {
		let lot = L.lots.pop();
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			newLotsAfterStreetDividesLot(newStreetDividingBoundingBlock(lot), lot).forEach(newLot => {
				if (lotIsClaimable(newLot)) {
					L.claimedLots.push(newLot);
				} else {
					L.lots.push(newLot);
				}
			});
		}
	}
}

subdivideLots();
addMonoliths(L.claimedLots);

And here’s one sample result (click to zoom in):

Figure 1. (Click to zoom in.)

Not bad! This map depicts a 60,800 foot × 49,100 foot region of Lacc. (That’s 11.5 miles × 9.3 miles, or 12,160 × 9,820 standard 5-ft. grid squares.) This is already quite large enough to create the illusion of a vast, unbounded space—and we can create as many such maps as we like.

The generator defaults to creating a map exactly as big as the browser viewport (i.e., the above map was generated by loading the demo in a browser window 1216 pixels wide by 982 pixels tall, resulting in a map 1216 units × 982 units in size; remember that 1 map unit here represents 50 feet), but that’s no intrinsic limitation; we can just as easily set the grid dimensions to something much larger—say, 10,000×10,000. That does, of course, make the code take correspondingly longer to run, and creates a correspondingly larger output file (warning: 48 MB SVG file). (A ~100-fold increase, in both cases, as both run time and output size scale linearly with area, the latter due to the fixed average monolith size and thus an expected monolith count proportional to area—the 1216×982-unit map above has ~18,000 monoliths, while the 10,000×10,000-unit map has ~1,500,000 monoliths.) A map of those dimensions represents a region of Lacc that is ~94.7 miles square, a.k.a. 100,000 standard grid squares to a side.

Not bad, as I said… but not great. The obvious flaw is that we only have one width of street represented, whereas what we’d like is a reasonable mix: a few great thoroughfares that run across great lengths of the map, some decently-wide connecting avenues between them, a bunch of medium-sized streets, and a whole lot of short little (well, “little” by the standards of the City of Monoliths) alleys.

Random street widths

We might first think to just make a minimal tweak to the above algorithm that gives each placed dividing street a random width (omitted sections of code are unchanged):

L = {
	minMonolithFootprint: 3,
	maxMonolithFootprint: 12
	streetWidths: {
		8: 0.01,
		4: 0.09,
		2: 0.25,
		1: 0.65
	}
};

function randomStreetWidth() {
	let dieSize = 100;
	let roll = rollDie(dieSize);

	let minRoll = dieSize + 1;
	for (let [ width, probability ] of Object.entries(L.streetWidths)) {
		minRoll -= probability * dieSize;
		if (roll >= minRoll)
			return parseInt(width);
	}
}

function newStreetDividingBoundingBlock(block) {
	let streetWidth;
	do {
		streetWidth = randomStreetWidth();
	} while (streetWidth > (Math.max(block.width, block.height) - L.maxMonolithFootprint));

	if (block.width > block.height) {
		return {
			width:  streetWidth,
			length: block.height,
			orientation: "v",
			x: (  block.x 
				+ L.minMonolithFootprint 
				+ rollDie(block.width - 2 * L.minMonolithFootprint - streetWidth)),
			y: block.y
		};
	} else {
		return {
			width:  streetWidth,
			length: block.width,
			orientation: "h",
			x: block.x,
			y: (  block.y 
				+ L.minMonolithFootprint 
				+ rollDie(block.height - 2 * L.minMonolithFootprint - streetWidth))
		};
	}
}

Notice that we’ve specified the distribution of street widths that our algorithm should sample from when attempting to place a street: 400-ft.-wide (a.k.a width of 8 units) streets—1%; 200-ft.-wide—9%; 100-ft.-wide—25%; 50-ft.-wide—65%. (The resulting distribution of street widths in the generated map will be somewhat different from this—more skewed toward narrower streets, to be precise—because the widths of dividable lots at each iteration will increasingly limit the average maximum width of a street that can fit in a lot).

Unfortunately, the result is not what we want:

Figure 2. (Click to zoom in.)

This looks wrong. The problem here is that wider streets should, in general, be longer than narrow streets; having broad avenues that go for only a tiny distance is weird—you never see this sort of thing in a real city. To be precise, what we want is for a street to be able to cut across any orthogonal-orientation street that is narrower than it. So the broadest avenues could span the whole map, while most of the small alleys would run only between the two nearest larger streets.

(Actually, is that quite right? Hold that thought; we’ll come back to it. For now, let’s take for granted the desideratum described in the previous paragraph.)

Drawing lots

Let’s try a different approach. Instead of iterating over lots and subdividing them, we will do the following:

1. Randomly select a street width and an orientation.
2. Selecting from only those lots in which a street of the selected width and orientation can fit (without resulting, after dividing the lot, in the creation of any lot that’s too small to contain a monolith), pick a random such lot.
   • If no lot can be found that fits a street of the selected width and orientation, go back to step 1.
3. Place the street in the selected lot (at a random position within the lot, selecting from only those positions that satisfy the constraint described in the previous step). (This will divide the lot into two lots.)
   • For each of the two newly created lots, check whether the lot is ready to have a monolith placed on it. If so, set it aside as claimed. Otherwise, place it back into the set of available lots.
4. If any available lots remain, repeat from step 1.

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12,

	streetWidths: {
		8: 0.02,
		4: 0.08,
		2: 0.25,
		1: 0.65
	}
};

function newLotsAfterStreetDividesLot(street, lot) {
	if (street.orientation == "h") {
		let topLot = {
			x:      lot.x,
			y:      lot.y,
			width:  lot.width,
			height: street.y - lot.y,
			left:   lot.left,
			right:  lot.right,
			top:    lot.top,
			bottom: street.y
		};
		let bottomLot = {
			x:      lot.x,
			y:      street.y + street.width,
			width:  lot.width,
			height: lot.bottom - (street.y + street.width),
			left:   lot.left,
			right:  lot.right,
			top:    street.y + street.width,
			bottom: lot.bottom
		};

		return [ topLot, bottomLot ];
	} else {
		let leftLot = {
			x:      lot.x,
			y:      lot.y,
			width:  street.x - lot.x,
			height: lot.height,
			left:   lot.left,
			right:  street.x,
			top:    lot.top,
			bottom: lot.bottom
		};
		let rightLot = {
			x:      street.x + street.width,
			y:      lot.y,
			width:  lot.right - (street.x + street.width),
			height: lot.height,
			left:   street.x + street.width,
			right:  lot.right,
			top:    lot.top,
			bottom: lot.bottom
		};

		return [ leftLot, rightLot ];
	}
}

function lotIsClaimable(lot) {
	return (   lot.width  <= L.maxMonolithFootprint
			&& lot.height <= L.maxMonolithFootprint);
}

function getRandomStreetWidth() {
	let dieSize = 100;
	let roll = rollDie(dieSize);

	let minRoll = dieSize + 1;
	for (let [ width, probability ] of Object.entries(L.streetWidths)) {
		minRoll -= probability * dieSize;
		if (roll >= minRoll)
			return parseInt(width);
	}
}

function getRandomOrientation() {
	return (rollDie(2) - 1) ? "h" : "v";
}

function getRandomLot(width, orientation) {
	let suitableLots = L.lots.filter(lot => {
		if (orientation == "h") {
			return lot.height >= 2 * L.minMonolithFootprint + width;
		} else {
			return lot.width >= 2 * L.minMonolithFootprint + width;
		}
	});

	let orientationString = orientation == "h" ? "horizontal" : "vertical";

	if (suitableLots.length == 0)
		return null;
	else
		return suitableLots[rollDie(suitableLots.length) - 1];
}

function getRandomPointInLot(lot, width, orientation) {
	if (lot == null)
		return null;

	if (orientation == "h") {
		return {
			x: lot.x + Math.floor(lot.width / 2),
			y: lot.y + L.minMonolithFootprint + rollDie(lot.height - 2 * L.minMonolithFootprint - width)
		};
	} else {
		return {
			x: lot.x + L.minMonolithFootprint + rollDie(lot.width - 2 * L.minMonolithFootprint - width),
			y: lot.y + Math.floor(lot.height / 2)
		};
	}
}

function placeRandomStreet() {
	if (L.lots.length == 0)
		return false;

	let width = getRandomStreetWidth();

	let orientation = getRandomOrientation();

	let lot = getRandomLot(width, orientation);
	let position = getRandomPointInLot(lot, width, orientation);

	if (position == null)
		return true;

	let length = orientation == "h" 
				 ? lot.width 
				 : lot.height;
	if (orientation == "h") {
		position.x = lot.x;
	} else {
		position.y = lot.y;
	}

	L.lots.remove(lot);
	newLotsAfterStreetDividesLot({
		width:  width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	}, lot).forEach(newLot => {
		if (lotIsClaimable(newLot)) {
			L.claimedLots.push(newLot);
		} else {
			L.lots.push(newLot);
		}
	});

	return true;
}

while(placeRandomStreet());

addMonoliths(L.claimedLots);

Figure 3. (Click to zoom in.)

We’re making progress! We’ve still got a lot of those short, wide streets, though…

Unbounded extension

Perhaps we can simply extend each street we place past the bounds of the lot we’re placing it in, all the way to the edges of the map? Of course, when placing a street, we will have to divide not only the lot we picked out, but all the other lots which that street will intersect. Like so (as before, unchanged code is omitted):

function placeRandomStreet() {
	if (L.lots.length == 0)
		return false;

	let width = getRandomStreetWidth();

	let orientation = getRandomOrientation();

	let lot = getRandomLot(width, orientation);
	let position = getRandomPointInLot(lot, width, orientation);

	if (position == null)
		return true;

	let length = orientation == "h" 
				 ? L.gridWidth 
				 : L.gridHeight;
	if (orientation == "h") {
		position.x = 0;
	} else {
		position.y = 0;
	}

	let newStreet = {
		width:  width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	};
	let lotsAfterSubdividing = [ ];
	for (let lot of L.lots) {
		if (streetIntersectsLot(newStreet, lot)) {
			lotsAfterSubdividing.push(...(newLotsAfterStreetDividesLot(newStreet, lot)));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}
	for (let lot of L.claimedLots) {
		if (streetIntersectsLot(newStreet, lot)) {
			lotsAfterSubdividing.push(...(newLotsAfterStreetDividesLot(newStreet, lot)));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}	
	L.lots = [ ];
	L.claimedLots = [ ];
	for (let lot of lotsAfterSubdividing) {
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.lots.push(lot);
		}
	}

	return true;
}

while(placeRandomStreet());

addMonoliths([ ...L.lots, ...L.claimedLots ]);

Figure 4. (Click to zoom in.)

Hmm. Not quite.

Top-down planning

Let’s revisit the question of which streets should be able to cut across which other streets. We said before that wider streets should be able to cut across narrower streets, but not vice-versa; but what does that actually mean? If street A intersects street B, then street B by definition also intersects street A. Yet there’s clearly something wrong with both figure 4 and figure 2 (and, to a slightly lesser extent, figure 3), which has to do with what streets intersect what others.

Recall what we said we want to see: “a few great thoroughfares that run across great lengths of the map, some decently-wide connecting avenues between them, a bunch of medium-sized streets, and a whole lot of short little alleys”. So, the widest streets should run all the way across the map, but a small alley should not run all the way across the map. One way to think about this is to imagine the city layout being planned in stages: first we place the widest streets, then we place slightly narrower streets in the lots between those widest streets (but never crossing the boundaries of those lots), then we place even narrower streets in the lots that remain, etc., until we’ve reached the narrowest street type, which we can continue placing until we’ve subdivided all the lots down to our desired size.

The problem with implementing this approach algorithmically is that having started placing streets of width 8, say, we don’t know when to stop—how many such streets should we have? When can we say “that’s enough streets of width 8, let’s now start placing streets of width 4”? Since we’re placing streets in order of width, we can’t rely on random sampling from a defined probability distribution to give us (an approximation to) the street width frequency distribution we’re going for.

However, perhaps we can cheat, by means of a simple heuristic. The code that produced figure 3 results in ~23,000 streets at a grid size of 1216×982 (that’s in width units representing 50 feet each, remember, not feet or grid squares). Let’s round that down to 20,000, and then simply create as many streets of each type as we estimate there should be, given our desired street width frequency distribution. (That distribution will not match the probability distributions we’ve been using in the previous code samples, because there, the width of a placed street was constrained by the average available lot size. Since that won’t meaningfully be the case any longer, we’ll have to adjust the frequencies significantly downwards for the larger street widths, e.g. there certainly cannot be 200 or 400 streets of width 8 on a 1216×982 map!)

A bit of tweaking of the frequencies, and we have (omitted code unchanged, as before):

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12,

	streetWidths: {
		8: 0.00002,
		4: 0.00028,
		2: 0.00470,
		1: 0.99500
	}
};

function placeRandomStreet(streetWidth) {
	if (L.lots.length == 0)
		return false;

	let width = streetWidth;

	let orientation = getRandomOrientation();

	let lot = getRandomLot(width, orientation);
	let position = getRandomPointInLot(lot, width, orientation);

	if (position == null)
		return true;

	let length = orientation == "h" 
				 ? lot.width 
				 : lot.height;
	if (orientation == "h") {
		position.x = lot.x;
	} else {
		position.y = lot.y;
	}

	let newStreet = {
		width:  width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	});

	let lotsAfterSubdividing = [ ];
	for (let lot of L.lots) {
		if (streetIntersectsLot(newStreet, lot)) {
			lotsAfterSubdividing.push(...(newLotsAfterStreetDividesLot(newStreet, lot)));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}
	L.lots = [ ];
	for (let lot of lotsAfterSubdividing) {
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.lots.push(lot);
		}
	}

	return true;
}

let totalNumStreets = 2E4;
let streetWidthsInReverseOrder = [ ...(Object.keys(L.streetWidths).sort()) ].reverse();
for (let width of streetWidthsInReverseOrder) {
	width = parseInt(width);
	let numStreetsOfThisWidth = L.streetWidths[width] * totalNumStreets;
	for (let i = 0; i < numStreetsOfThisWidth; i++)
		placeRandomStreet(width);
}

addMonoliths([ ...L.lots, ...L.claimedLots ]);

Figure 5. (Click to zoom in.)

We’re making progress!

We’ve got a bunch of un-subdivided lots in there, though (the large blocks of black). Those definitely exceed our defined monolith size ranges. Now, we could adjust our anticipated total street count upwards, and tweak the defined street width frequency distribution… but that seems like a very fragile solution (even more so than the heuristic we’re already using).

A mixed approach

For a more robust fix, let’s bring back the approach we started with (which generated the map shown in figure 5): subdividing lots until all lots are suitably small. We will do this after we have placed all the streets as per the previous code sample:

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12,

	streetWidths: {
		8: 0.00002,
		4: 0.00028,
		2: 0.00470,
		1: 0.99500
	}
};

function placeRandomStreet(streetWidth) {
	if (L.lots.length == 0)
		return false;

	let width = streetWidth;

	let orientation = getRandomOrientation();

	let lot = getRandomLot(width, orientation);
	let position = getRandomPointInLot(lot, width, orientation);

	if (position == null)
		return true;

	let length = orientation == "h" 
				 ? lot.width 
				 : lot.height;
	if (orientation == "h") {
		position.x = lot.x;
	} else {
		position.y = lot.y;
	}

	let newStreet = {
		width:  width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	});

	let lotsAfterSubdividing = [ ];
	for (let lot of L.lots) {
		if (streetIntersectsLot(newStreet, lot)) {
			lotsAfterSubdividing.push(...(newLotsAfterStreetDividesLot(newStreet, lot)));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}
	L.lots = [ ];
	for (let lot of lotsAfterSubdividing) {
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.lots.push(lot);
		}
	}

	return true;
}

function newStreetDividingBoundingBlock(block) {
	let streetWidth = 1;
	if (block.width > block.height) {
		return {
			width:  streetWidth,
			length: block.height,
			orientation: "v",
			x: (  block.x 
				+ L.minMonolithFootprint 
				+ rollDie(block.width - 2 * L.minMonolithFootprint - streetWidth)),
			y: block.y
		};
	} else {
		return {
			width:  streetWidth,
			length: block.width,
			orientation: "h",
			x: block.x,
			y: (  block.y 
				+ L.minMonolithFootprint 
				+ rollDie(block.height - 2 * L.minMonolithFootprint - streetWidth))
		};
	}
}

function subdivideLots() {
	while (L.lots.length > 0) {
		let lot = L.lots.pop();
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.streets.push(newStreetDividingBoundingBlock(lot));
			newLotsAfterStreetDividesLot(L.streets.last, lot).forEach(newLot => {
				if (lotIsClaimable(newLot)) {
					L.claimedLots.push(newLot);
				} else {
					L.lots.push(newLot);
				}
			});
		}
	}
}

let totalNumStreets = 2E4;
let streetWidthsInReverseOrder = [ ...(Object.keys(L.streetWidths).sort()) ].reverse();
for (let width of streetWidthsInReverseOrder) {
	width = parseInt(width);
	let numStreetsOfThisWidth = L.streetWidths[width] * totalNumStreets;
	for (let i = 0; i < numStreetsOfThisWidth; i++)
		placeRandomStreet(width);
}

subdivideLots();

addMonoliths([ ...L.lots, ...L.claimedLots ]);

Figure 6. (Click to zoom in.)

Definitely starting to get somewhere.

One problematic behavior that this algorithm has is that it often places parallel wide streets much closer to one another than is plausible. You can see many cases of this in the preceding two samples, e.g.:

Figure 7. (Click to zoom in.)

Breathing room

So let’s explicitly correct for this. We’ll introduce a “repulsion factor”, which will prevent streets from being too close to each other. Streets will repel one another in proportion to width—specifically, the width of the narrower of two streets. Thus, a narrow street can be close to a narrow street, or to a wide street; but two wide streets must be further apart. Each time we pick a random location to place a street, we’ll check whether it’s too close to another street, according to this repulsion factor; if so, we’ll try again with another random location.

And so (unchanged code omitted, as before):

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12,

	streetWidths: {
		8: 0.00010,
		4: 0.00090,
		2: 0.00900,
		1: 0.99000
	},

	streetRepulsionFactor: 10
};

function streetsBoundingLot(lot) {
	let boundingStreets = L.streets.filter(street => {
		if (street.orientation == "h") {
			return (   (   street.y + street.width == lot.top
						|| lot.bottom == street.y)
					&& (   street.x < lot.right
						&& street.x + street.length > lot.left));

		} else {
			return (   (   street.x + street.width == lot.left
						|| lot.right == street.x)
					&& (   street.y < lot.bottom
						&& street.y + street.length > lot.top));
		}
	});

	let streets = {
		all: boundingStreets
	};
	for (let boundingStreet of boundingStreets) {
		if (boundingStreet.y + boundingStreet.width == lot.top)
			streets.top = boundingStreet;
		if (lot.bottom == boundingStreet.y)
			streets.bottom = boundingStreet;
		if (boundingStreet.x + boundingStreet.width == lot.left)
			streets.left = boundingStreet;
		if (lot.right == boundingStreet.x)
			streets.right = boundingStreet;
	}

	return streets;
}

function placeRandomStreet(streetWidth) {
	if (L.lots.length == 0)
		return false;

	let width = streetWidth;

	let orientation = getRandomOrientation();

	let lot = getRandomLot(width, orientation);
	let position = getRandomPointInLot(lot, width, orientation);

	if (position == null)
		return false;

	let boundingStreets = streetsBoundingLot(lot);
	if (orientation == "h") {
		let spaceAbove = position.y - (boundingStreets.top.y + boundingStreets.top.width);
		let spaceBelow = boundingStreets.bottom.y - (position.y + width);

		let minSpaceAbove = Math.max(L.minMonolithFootprint, 
									 Math.min(width, boundingStreets.top.width || width)    * L.streetRepulsionFactor);
		let minSpaceBelow = Math.max(L.minMonolithFootprint,
									 Math.min(width, boundingStreets.bottom.width || width) * L.streetRepulsionFactor);

		if (   spaceAbove < minSpaceAbove
			|| spaceBelow < minSpaceBelow)
			return false;
	} else {
		let spaceLeft = position.x - (boundingStreets.left.x + boundingStreets.left.width);
		let spaceRight = boundingStreets.right.x - (position.x + width);

		let minSpaceLeft = Math.max(L.minMonolithFootprint, 
									Math.min(width, boundingStreets.left.width || width)   * L.streetRepulsionFactor);
		let minSpaceRight = Math.max(L.minMonolithFootprint,
									 Math.min(width, boundingStreets.right.width || width) * L.streetRepulsionFactor);

		if (   spaceLeft  < minSpaceLeft
			|| spaceRight < minSpaceRight)
			return false;
	}

	let length = orientation == "h" 
				 ? lot.width 
				 : lot.height;
	if (orientation == "h") {
		position.x = lot.x;
	} else {
		position.y = lot.y;
	}

	L.streets.push({
		width:  width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	});

	let lotsAfterSubdividing = [ ];
	for (let lot of L.lots) {
		if (streetIntersectsLot(L.streets.last, lot)) {
			lotsAfterSubdividing.push(...(newLotsAfterStreetDividesLot(L.streets.last, lot)));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}
	L.lots = [ ];
	for (let lot of lotsAfterSubdividing) {
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.lots.push(lot);
		}
	}

	return true;
}

let totalNumStreets = 2E4;
let streetWidthsInReverseOrder = [ ...(Object.keys(L.streetWidths).sort()) ].reverse();
for (let width of streetWidthsInReverseOrder) {
	width = parseInt(width);
	let desiredNumStreetsOfThisWidth = L.streetWidths[width] * totalNumStreets;
	let numStreetsOfThisWidth = 0;
	if (width > 1) {
		while (numStreetsOfThisWidth < desiredNumStreetsOfThisWidth) {
			if (placeRandomStreet(width))
				numStreetsOfThisWidth++;
		}
	} else {
		for (let i = 0; i < desiredNumStreetsOfThisWidth; i++)
			placeRandomStreet(width);
	}
}

subdivideLots();

addMonoliths(L.claimedLots);

Figure 8. (Click to zoom in.)

Not too bad.

We’ve definitely reached the point where we can generate maps (in as great a quantity as we please) which have the property that they locally look plausible at pretty much any point, and offer a variety of types of street configurations (from great highways with smaller avenues branching off them, to haphazardly-arranged warrens of alleys). In other words, this is already usable for the purpose of picking an arbitrary location somewhere in the middle of the map and setting an encounter there (which is what we wanted in the first place).

Still, there are some problems. One obvious problem is that the algorithm is fragile and contains multiple “magic numbers” which must be tweaked in an ad-hoc manner to produce desired results—an expected street count (which doesn’t even end up matching the street count in the resulting map; the map shown in figure 8, for example, has ~15,000 streets, not ~20,000), and a carefully tweaked expected street width frequency distribution (which also doesn’t end up matching the actual frequency distribution of streets in the resulting map). The former, in particular, has to be adjusted for different map sizes (though perhaps we could pick a reasonably suitable number automatically as some function of map size…). Robust and flexible, it ain’t.

Even setting aside implementation details, though, something about this map (and this is true of basically all maps created by this version of the algorithm) looks wrong—unnatural, somehow. This is not necessarily a problem for our very specific motivating purpose (using one or more such maps as settings for random encounters while traveling through the City of Monoliths)… but, as with our other design decisions so far, it would be better if every aspect of the design contributed to the feel of the adventure, while avoiding any visibly artificial-seeming elements.

Clumping

Why does the map shown in figure 8 look vaguely wrong? On close inspection, we can see that it has two odd properties. First, this algorithm has a tendency to subdivide some parts of the map many times (producing regions with many streets of intermediate width and heterogeneous sizes of “blocks” between them), while leaving other parts of the map relatively uniform (producing large regions with only small alleys, and no intermediate-width streets crossing them).

This is easier to see if we pause the generator in the middle of the process, before any streets of width 1 have been placed. Here’s one map with only streets of width 2 or greater:

Figure 9. (Click to zoom in.)

And here’s a map with only streets of width 4 or greater:

Figure 10. (Click to zoom in.)

Whether this effect is good or bad by itself is probably a question of aesthetics (although in combination with the next quirk, it’s definitely bad). But why does it happen? Actually, that’s a pretty straightforward mathematical consequence of how the street-placement algorithm works. Remember that when placing a street, we select a random point at which to (attempt to) place the street by first picking an un-subdivided lot at random, with the distribution across lots being uniform and—importantly—not weighted by lot size. Now suppose that we place two streets, like this:

Figure 11. (Click to zoom in.)

We now have three lots—and each of them has an equal chance to be selected for attempted street placement! The top two lots together cover a smaller area than the bottom lot, and the top-left lot covers a smaller area than the top-right lot—which means that, when selecting a random lot to place a street in, that street is more likely to be placed closer to the top edge of the map than to the bottom edge, and more likely to be placed closer to the left edge of the map than to the right edge. And the more streets we place in some region of the map, the more lots we create there, and the more likely it becomes that further streets will be placed in that region, etc. Of course, the relatively likelihood that a street will be place in some part of the map levels off once the repulsion effect and the minimum lot size rule start to prevent streets from being placed in more and more of the randomly chosen points in that part of the map… but by then, most or all of the widest and intermediate-width streets have been placed, and the skew in the distribution of street widths by map region is already in place.

Whither crossroads?

The other odd property of maps generated by this algorithm can be seen if we take a close look at the map in figure 8. Take a look at the intersections between streets. Notice anything odd?

There are almost no X-intersections (a.k.a. crossroads).

There’s plenty of T-intersections, of course. But very few where two streets cross and both of them continue in both directions—and only one such intersection involving streets of width greater than 1!

This is, actually, pretty weird. Real cities tend to have plenty of X-intersections; their near-total absence from this map is a large part of what makes it look vaguely artificial. The way this algorithm is written means that narrower streets can never cut across wider streets… but that turns out to mean that the reverse is also true, with the result that streets don’t cut across one another at all. (The few existing X-intersections are created by coincidence—each consists not of two streets, but of three, with two coincidentally-collinear streets meeting, at the same point, a third which is orthogonal to the other two.)

Another way to look at the city layout that results from this is that there is no way out of a region of the map except by traversing increasingly wide avenues. In effect, there are no “take the local streets” routes as alternatives to the major thoroughfares. This has the effect of making the map less interesting on a large scale. (Again, this is not relevant for the very specific purpose of using the map to run disjoint encounters, each of which is localized to a small sub-region; however, it would be preferable if these maps we are generating could stand up to a bit more prodding and “off-label use” without their Potemkin facades collapsing.)

Robert Moses would approve

Let’s take a third crack at the idea that wide streets should be able to cut across narrower streets, but not vice-versa. Consider what happens if we once again place streets not in descending width order, but randomly (as in figure 3), allowing a street to extend past the ends of the lot we placed it in (unlike in figure 3), but not necessarily all the way to the edges of the map (unlike in figure 4). Instead, we will extend each street, in either direction, only until it hits another street of the same width or wider (or the edge of the map).²

The full code (sans boilerplate / utility functions):

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12,

	streetWidths: {
		8: 0.02,
		4: 0.08,
		2: 0.25,
		1: 0.65
	},

	streetRepulsionFactor: 10,
};

L.lots = [ { x:      0,
			 y:      0,
			 width:  L.gridWidth,
			 height: L.gridHeight,
			 left:   0,
			 right:  L.gridWidth,
			 top:    0,
			 bottom: L.gridHeight
			 } ];
L.claimedLots = [ ];
L.streets = [
	{ width: 0,
	  length: L.gridWidth,
	  orientation: "h",
	  x: 0,
	  y: 0
	  },
	{ width: 0,
	  length: L.gridHeight,
	  orientation: "v",
	  x: 0,
	  y: 0
	  },
	{ width: 0,
	  length: L.gridWidth,
	  orientation: "h",
	  x: 0,
	  y: L.gridHeight
	  },
	{ width: 0,
	  length: L.gridHeight,
	  orientation: "v",
	  x: L.gridWidth,
	  y: 0
	  }
];

function newLotsAfterStreetDividesLot(street, lot) {
	let newLots = [ ];

	if (street.orientation == "h") {
		let topLot = {
			x:      lot.x,
			y:      lot.y,
			width:  lot.width,
			height: street.y - lot.y,
			left:   lot.left,
			right:  lot.right,
			top:    lot.top,
			bottom: street.y
		};
		let bottomLot = {
			x:      lot.x,
			y:      street.y + street.width,
			width:  lot.width,
			height: lot.bottom - (street.y + street.width),
			left:   lot.left,
			right:  lot.right,
			top:    street.y + street.width,
			bottom: lot.bottom
		};

		if (topLot.width    * topLot.height    > 0)
			newLots.push(topLot);

		if (bottomLot.width * bottomLot.height > 0)
			newLots.push(bottomLot);
	} else {
		let leftLot = {
			x:      lot.x,
			y:      lot.y,
			width:  street.x - lot.x,
			height: lot.height,
			left:   lot.left,
			right:  street.x,
			top:    lot.top,
			bottom: lot.bottom
		};
		let rightLot = {
			x:      street.x + street.width,
			y:      lot.y,
			width:  lot.right - (street.x + street.width),
			height: lot.height,
			left:   street.x + street.width,
			right:  lot.right,
			top:    lot.top,
			bottom: lot.bottom
		};

		if (leftLot.width  * leftLot.height  > 0)
			newLots.push(leftLot);

		if (rightLot.width * rightLot.height > 0)
			newLots.push(rightLot);
	}

	return newLots;
}

function lotIsClaimable(lot) {
	return (   lot.width  <= L.maxMonolithFootprint
			&& lot.height <= L.maxMonolithFootprint);
}

function getRandomStreetWidth() {
	let dieSize = 100;
	let roll = rollDie(dieSize);

	let minRoll = dieSize + 1;
	for (let [ width, probability ] of Object.entries(L.streetWidths)) {
		minRoll -= probability * dieSize;
		if (roll >= minRoll)
			return parseInt(width);
	}
}

function getRandomOrientation() {
	return (rollDie(2) - 1) ? "h" : "v";
}

function getRandomLot(width, orientation) {
	let suitableLots = L.lots.filter(lot => {
		if (orientation == "h") {
			return lot.height >= 2 * L.minMonolithFootprint + width;
		} else {
			return lot.width >= 2 * L.minMonolithFootprint + width;
		}
	});

	let orientationString = orientation == "h" ? "horizontal" : "vertical";

	if (suitableLots.length == 0)
		return null;
	else
		return suitableLots[rollDie(suitableLots.length) - 1];
}

function getRandomPointInLot(lot, width, orientation) {
	if (lot == null)
		return null;

	if (orientation == "h") {
		return {
			x: lot.x + Math.floor(lot.width / 2),
			y: lot.y + L.minMonolithFootprint + rollDie(lot.height - 2 * L.minMonolithFootprint - width)
		};
	} else {
		return {
			x: lot.x + L.minMonolithFootprint + rollDie(lot.width - 2 * L.minMonolithFootprint - width),
			y: lot.y + Math.floor(lot.height / 2)
		};
	}
}

function getRandomPoint(width, orientation) {
	return getRandomPointInLot(getRandomLot(width, orientation), width, orientation);
}

function getBoundingBlockAtPoint(point, options) {
	options = Object.assign({
		streetWidth: 1,
		orientation: null
	}, options);

	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >= options.streetWidth 
		   	)
		&& street.orientation != options.orientation
	);

	let compareFunction = (a, b) => {
		if (a.orientation == "v") {
			if (a.x < b.x)
				return -1;
			if (a.x > b.x)
				return 1;
			return 0;
		} else {
			if (a.y < b.y)
				return -1;
			if (a.y > b.y)
				return 1;
			return 0;
		}
	};

	let nearestStreetLeft, nearestStreetRight, nearestStreetAbove, nearestStreetBelow;
	let blockLeft, blockTop, blockRight, blockBottom;

	let lotAtPoint = L.lots.find(lot => 
		   lot.left   <= point.x
		&& lot.right  >= point.x
		&& lot.top    <= point.y
		&& lot.bottom >= point.y
	);
	if (lotAtPoint == null)
		return null;

	if (options.orientation == "h") {
		nearestStreetLeft = crossStreets.filter(street => 
			   street.x <= point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).last;
		nearestStreetRight = crossStreets.filter(street => 
			   street.x > point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).first;

		blockLeft = nearestStreetLeft.x + nearestStreetLeft.width;
		blockRight = nearestStreetRight.x;

		blockTop = lotAtPoint.top;
		blockBottom = lotAtPoint.bottom;
	} else {
		nearestStreetAbove = crossStreets.filter(street =>
			   street.y <= point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).last;
		nearestStreetBelow = crossStreets.filter(street => 
			   street.y > point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).first;

		blockTop = nearestStreetAbove.y + nearestStreetAbove.width;
		blockBottom = nearestStreetBelow.y;

		blockLeft = lotAtPoint.left;
		blockRight = lotAtPoint.right;
	}

	return {
		x:      blockLeft,
		y:      blockTop,
		width:  blockRight - blockLeft,
		height: blockBottom - blockTop,
		left:   blockLeft,
		right:  blockRight,
		top:    blockTop,
		bottom: blockBottom
	}
}

function streetIntersectsLot(street, lot) {
	if (street.orientation == "h") {
		if (   street.x < lot.right
			&& street.x + street.length > lot.x
			&& street.y < lot.bottom
			&& street.y + street.width > lot.y)
			return true;
	} else {
		if (   street.y < lot.bottom
			&& street.y + street.length > lot.y
			&& street.x < lot.right
			&& street.x + street.width > lot.x)
			return true;
	}

	return false;
}

function placeRandomStreet() {
	if (L.lots.filter(lot => lot.width * lot.height > 0).length == 0)
		return false;

	let width = getRandomStreetWidth();

	let orientation = getRandomOrientation();

	let position = getRandomPoint(width, orientation);
	if (position == null)
		return true;

	let boundingBlock = getBoundingBlockAtPoint(position, {
		streetWidth: width,
		orientation: orientation
	});

	if (boundingBlock == null)
		return true;

	let length = orientation == "h" 
				 ? boundingBlock.width 
				 : boundingBlock.height;

	if (orientation == "h") {
		position.x = boundingBlock.x;
	} else {
		position.y = boundingBlock.y;
	}

	L.streets.push({
		width: width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	});

	let lotsAfterSubdividing = [ ];
	for (let lot of [ ...L.lots, ...L.claimedLots ]) {
		if (streetIntersectsLot(L.streets.last, lot)) {
			lotsAfterSubdividing.push(...newLotsAfterStreetDividesLot(L.streets.last, lot));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}
	L.lots = [ ];
	L.claimedLots = [ ];
	for (let lot of lotsAfterSubdividing) {
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.lots.push(lot);
		}
	}

	return true;
}

while(placeRandomStreet());

addMonoliths(L.claimedLots);

And the result:

Figure 12. (Click to zoom in.)

Hmm. Something has gone wrong here. On closer inspection, we can see that most of what at first look like very wide streets, are actually just narrower streets that run directly adjacent to each other (or even overlapping) for some part of their lengths. But how can this be, given that we explicitly check for proximity of a street to the edges of the lot that it’s placed in? Well, that’s the problem, actually: we check for proximity to the edges of the lot it’s placed in, but we’ve just decided to extend streets in both directions past the ends of the lots they’re placed in—and we aren’t checking for proximity to the edges of those other lots that the street will pass through!

Breathing room, redux

So we’ll add an explicit check for that (as usual, omitted code is unchanged):

function getBoundingBlockAtPoint(point, options) {
	options = Object.assign({
		streetWidth: 1,
		orientation: null
	}, options);

	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >= options.streetWidth 
		   	)
		&& street.orientation != options.orientation
	);
	let parallelStreets = L.streets.filter(street => 
		street.orientation == options.orientation
	);

	let compareFunction = (a, b) => {
		if (a.orientation == "v") {
			if (a.x < b.x)
				return -1;
			if (a.x > b.x)
				return 1;
			return 0;
		} else {
			if (a.y < b.y)
				return -1;
			if (a.y > b.y)
				return 1;
			return 0;
		}
	};

	let nearestStreetLeft, nearestStreetRight, nearestStreetAbove, nearestStreetBelow;
	let blockLeft, blockTop, blockRight, blockBottom;

	if (options.orientation == "h") {
		nearestStreetLeft = crossStreets.filter(street => 
			   street.x <= point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).last;
		nearestStreetRight = crossStreets.filter(street => 
			   street.x > point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).first;

		blockLeft = nearestStreetLeft.x + nearestStreetLeft.width;
		blockRight = nearestStreetRight.x;

		nearestStreetAbove = parallelStreets.filter(street => 
			   street.x < blockRight
			&& street.x + street.length >= blockLeft
			&& street.y <= point.y
		).sort(compareFunction).last;
		nearestStreetBelow = parallelStreets.filter(street => 
			   street.x < blockRight
			&& street.x + street.length >= blockLeft
			&& street.y > point.y
		).sort(compareFunction).first;

		let spaceAbove = point.y - (nearestStreetAbove.y + nearestStreetAbove.width);
		let spaceBelow = nearestStreetBelow.y - (point.y + options.streetWidth);

		let minSpaceAbove = Math.max(L.minMonolithFootprint, 
									 Math.min(options.streetWidth, nearestStreetAbove.width || options.streetWidth) * L.streetRepulsionFactor);
		let minSpaceBelow = Math.max(L.minMonolithFootprint,
									 Math.min(options.streetWidth, nearestStreetBelow.width || options.streetWidth) * L.streetRepulsionFactor);

		if (   spaceAbove < minSpaceAbove
			|| spaceBelow < minSpaceBelow) {
			return null;
		} else {
			blockTop = nearestStreetAbove.y + nearestStreetAbove.width;
			blockBottom = nearestStreetBelow.y;
		}
	} else {
		nearestStreetAbove = crossStreets.filter(street =>
			   street.y <= point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).last;
		nearestStreetBelow = crossStreets.filter(street => 
			   street.y > point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).first;

		blockTop = nearestStreetAbove.y + nearestStreetAbove.width;
		blockBottom = nearestStreetBelow.y;

		nearestStreetLeft = parallelStreets.filter(street => 
			   street.y < blockBottom
			&& street.y + street.length >= blockTop
			&& street.x <= point.x
		).sort(compareFunction).last;
		nearestStreetRight = parallelStreets.filter(street => 
			   street.y < blockBottom
			&& street.y + street.length >= blockTop
			&& street.x > point.x
		).sort(compareFunction).first;

		let spaceLeft = point.x - (nearestStreetLeft.x + nearestStreetLeft.width);
		let spaceRight = nearestStreetRight.x - (point.x + options.streetWidth);

		let minSpaceLeft  = Math.max(L.minMonolithFootprint, 
									 Math.min(options.streetWidth, nearestStreetLeft.width  || options.streetWidth) * L.streetRepulsionFactor);
		let minSpaceRight = Math.max(L.minMonolithFootprint,
									 Math.min(options.streetWidth, nearestStreetRight.width || options.streetWidth) * L.streetRepulsionFactor);

		if (   spaceLeft  < minSpaceLeft
			|| spaceRight < minSpaceRight) {
			return null;
		} else {
			blockLeft = nearestStreetLeft.x + nearestStreetLeft.width;
			blockRight = nearestStreetRight.x;
		}
	}

	return {
		x:      blockLeft,
		y:      blockTop,
		width:  blockRight - blockLeft,
		height: blockBottom - blockTop,
		left:   blockLeft,
		right:  blockRight,
		top:    blockTop,
		bottom: blockBottom
	}
}

However, when we run this code, it seems to hang. On closer investigation, it’s actually running just fine—but because of the check that we’ve added, the algorithm will, at a certain point, start failing to find a suitable street placement (i.e., discovering that the randomly chosen point at which to attempt street placement is actually such that a street of the randomly chosen width and orientation cannot be placed there without passing impermissibly close to an edge of one or more lots) almost all the time, and finding a suitable placement more and more rarely. To illustrate this, we add a bit of debugging output:

function placeRandomStreet() {
	// … code omitted …

	if (boundingBlock == null) {
		console.log("Bounding block is null!");
		return true;
	}

	// … code omitted …

	console.log(`Placed a street (${L.streets.length} streets total). ${L.lots.length} lots remain.`);

	return true;
}

And this is what we see after less than a minute of runtime:

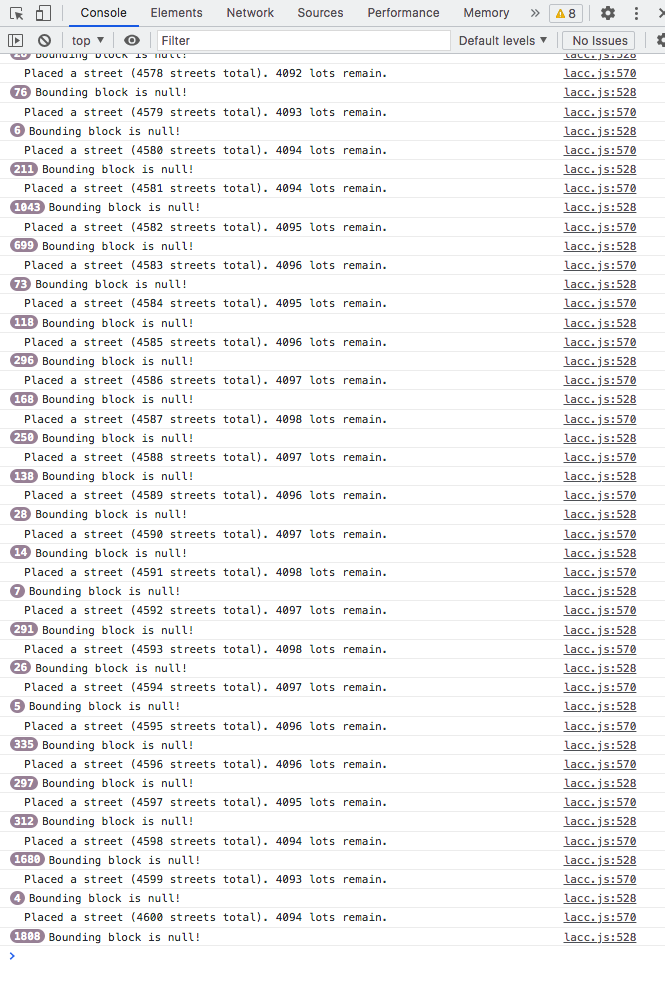
Figure 13. (Click to zoom in.)

If we wait for this to complete, we’ll be here all day…

Stopping halfway

Well, what happens if we stop the process after placing, let’s say, 4,000 streets? (The number is obviously chosen in an ad-hoc manner, and that won’t do for the actual implementation, but we’re just experimenting here.) The code still takes uncomfortably long to get even that far (around 15 seconds—much too long for a procgen like this), but:

Figure 14. (Click to zoom in.)

This seems fine. Of course most of the lots are bigger than we need them to be, but that is fixable, with the subdivision technique we’ve already used. And so:

Figure 15. (Click to zoom in.)

Nice! This is basically what we’re looking for. We’ve certainly solved our problem with the lack of X-intersections. The street clumping problem remains, but we’ll get to that later. First, though: how do we fix this excessive runtime? And how can we pick a stopping point in a less ad-hoc and arbitrary way than simply picking a street count? (Which would be map-size-dependent, anyhow.)

Roll to give up

We can use probabilistic stopping. That is: whenever we pick a random point (and random street width and orientation) and fail to place a street there (because of impermissible proximity to the edges of one or more of the lots the street would cross, if extended as far as it can be), we will roll a die (a 10,000-sized die, let’s say). If the die comes up anything but 1, we’ll keep trying; if it comes up 1, we’ll give up, and declare that random street placement is concluded.³ (At this point, we subdivide all remaining too-large lots with streets of width 1, as before.)

The modification to the code is trivial:

L = {
	//	… other configuration fields omitted …

	keepTryingHowHard: 10000
};

function placeRandomStreet() {
	// … code omitted …

	if (boundingBlock == null) {
		return (rollDie(L.keepTryingHowHard) != 1);
	}

	// … code omitted …
}

Figure 16. (Click to zoom in.)

Cool. Now the code finishes in couple of seconds at most—mission accomplished.

Cornstarch added to prevent

We’re very close to perfection now, but let’s see if we can solve that “street clumping” problem. Recall that this was caused by the fact that we are selecting a random lot to place a street in, which means that if the left half of the map has 10 lots and the right half has one big lot, then new streets are 10 times more likely to be placed on the left half of the map than on the right half, which results in the left half having even more lots and thus being even more likely to have new streets placed there… etc.

Well, one obvious solution is to instead select a point at random from a uniform distribution of all grid locations. (We will, of course, have to check that the point we’ve selected isn’t on a street instead of being within any lot, but that is easy enough.) Thus (omitted code unchanged, as usual):

function getRandomGridPoint() {
	return {
		x: rollDie(L.gridWidth) - 1,
		y: rollDie(L.gridHeight) - 1
	};
}

function pointIsOnStreet(point, street) {
	if (street.orientation == "h") {
		return (   point.x >= street.x
				&& point.x < street.x + street.length
				&& point.y >= street.y
				&& point.y < street.y + street.width);
	} else {
		return (   point.x >= street.x
				&& point.x < street.x + street.width
				&& point.y >= street.y
				&& point.y < street.y + street.length);
	}
}

function getBoundingBlockAtPoint(point, options) {
	options = Object.assign({
		streetWidth: 1,
		orientation: null
	}, options);

	if (L.streets.findIndex(street => pointIsOnStreet(point, street)) !== -1)
		return null;
	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >= options.streetWidth 
		   	)
		&& street.orientation != options.orientation
	);
	let parallelStreets = L.streets.filter(street => 
		street.orientation == options.orientation
	);

	let compareFunction = (a, b) => {
		if (a.orientation == "v") {
			if (a.x < b.x)
				return -1;
			if (a.x > b.x)
				return 1;
			return 0;
		} else {
			if (a.y < b.y)
				return -1;
			if (a.y > b.y)
				return 1;
			return 0;
		}
	};

	let nearestStreetLeft, nearestStreetRight, nearestStreetAbove, nearestStreetBelow;
	let blockLeft, blockTop, blockRight, blockBottom;

	if (options.orientation == "h") {
		nearestStreetLeft = crossStreets.filter(street => 
			   street.x <= point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).last;
		nearestStreetRight = crossStreets.filter(street => 
			   street.x > point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).first;

		blockLeft = nearestStreetLeft.x + nearestStreetLeft.width;
		blockRight = nearestStreetRight.x;

		nearestStreetAbove = parallelStreets.filter(street => 
			   street.x < blockRight
			&& street.x + street.length >= blockLeft
			&& street.y <= point.y
		).sort(compareFunction).last;
		nearestStreetBelow = parallelStreets.filter(street => 
			   street.x < blockRight
			&& street.x + street.length >= blockLeft
			&& street.y > point.y
		).sort(compareFunction).first;

		let spaceAbove = point.y - (nearestStreetAbove.y + nearestStreetAbove.width);
		let spaceBelow = nearestStreetBelow.y - (point.y + options.streetWidth);

		let minSpaceAbove = Math.max(L.minMonolithFootprint, 
									 Math.min(options.streetWidth, nearestStreetAbove.width || options.streetWidth) * L.streetRepulsionFactor);
		let minSpaceBelow = Math.max(L.minMonolithFootprint,
									 Math.min(options.streetWidth, nearestStreetBelow.width || options.streetWidth) * L.streetRepulsionFactor);

		if (   spaceAbove < minSpaceAbove
			|| spaceBelow < minSpaceBelow) {
			return null;
		} else {
			blockTop = nearestStreetAbove.y + nearestStreetAbove.width;
			blockBottom = nearestStreetBelow.y;
		}
	} else {
		nearestStreetAbove = crossStreets.filter(street =>
			   street.y <= point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).last;
		nearestStreetBelow = crossStreets.filter(street => 
			   street.y > point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).first;

		blockTop = nearestStreetAbove.y + nearestStreetAbove.width;
		blockBottom = nearestStreetBelow.y;

		nearestStreetLeft = parallelStreets.filter(street => 
			   street.y < blockBottom
			&& street.y + street.length >= blockTop
			&& street.x <= point.x
		).sort(compareFunction).last;
		nearestStreetRight = parallelStreets.filter(street => 
			   street.y < blockBottom
			&& street.y + street.length >= blockTop
			&& street.x > point.x
		).sort(compareFunction).first;

		let spaceLeft = point.x - (nearestStreetLeft.x + nearestStreetLeft.width);
		let spaceRight = nearestStreetRight.x - (point.x + options.streetWidth);

		let minSpaceLeft  = Math.max(L.minMonolithFootprint, 
									 Math.min(options.streetWidth, nearestStreetLeft.width  || options.streetWidth) * L.streetRepulsionFactor);
		let minSpaceRight = Math.max(L.minMonolithFootprint,
									 Math.min(options.streetWidth, nearestStreetRight.width || options.streetWidth) * L.streetRepulsionFactor);

		if (   spaceLeft  < minSpaceLeft
			|| spaceRight < minSpaceRight) {
			return null;
		} else {
			blockLeft = nearestStreetLeft.x + nearestStreetLeft.width;
			blockRight = nearestStreetRight.x;
		}
	}

	return {
		x:      blockLeft,
		y:      blockTop,
		width:  blockRight - blockLeft,
		height: blockBottom - blockTop,
		left:   blockLeft,
		right:  blockRight,
		top:    blockTop,
		bottom: blockBottom
	}
}

Figure 17. (Click to zoom in.)

Excellent. The street clumping problem has been banished. We have the result we want.

Optional Manhattanization

One final thought: in our current implementation, we allow streets to cut across existing streets that are narrower (than the street being placed). What if we tweaked this condition? The relevant part of the code is this, in the getBoundingBlockAtPoint() function:

	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >= options.streetWidth 
		   	)
		&& street.orientation != options.orientation
	);

Here’s the kind of thing we get if we allow streets to cut across existing streets that are narrower or as narrow:

	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >  options.streetWidth 
		   	)
		&& street.orientation != options.orientation
	);

Figure 18. (Click to zoom in.)

And here’s what we get if we allow streets to cut across existing streets that are at most twice as wide:

	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >  options.streetWidth * 2
		   	)
		&& street.orientation != options.orientation
	);

Figure 19. (Click to zoom in.)

Probably this isn’t very useful, but the option is there, if we want it.

(If we allow streets to cut across existing streets of any width, we simply get figure 4, of course.)

The algorithm

It may seem otherwise from the lengthy discussion thus far, but this really is a simple approach. (One might even call it “simplistic”. There isn’t anything very clever about this algorithm, and there’s no particular reason to be impressed by it. But it works well.)

1. Start trying to place streets of random width and orientation at random points on the grid, checking to make sure they don’t run too close to any other streets. Each time you fail to place a street, roll a big die; if you roll a 1, give up and go to the next step.
2. Find any lots (i.e., blocks of un-divided space) that are bigger than the minimum lot size, and divide them into two lots (at a random split point, down the shorter axis of the lot). Keep doing this until there are no too-big lots remaining.
3. You’re done! Render to the output format, display, save, whatever.

Implementation details

How should we save these maps, by the way? I’ve chosen SVG for the output format, because it’s widely supported, editable, usable for other purposes (see the next part of this series), and convertible into bitmap format, if need be. I see no compelling arguments for doing it in any other way.

There is one small detail of the output format which is a bit less obvious. What exactly should be represented? “Just monoliths” is one possible answer; “just streets” is another; “both” is a third. (Note that this question arises only because we’re using a vector file format; in a bitmap image, these three cases are completely indistinguishable given the constraints we’ve imposed on the generated map.)

I think that monoliths have to be represented (because it is otherwise unnecessarily tedious to derive the set of monolith coordinates from the set of street parameters), but whether streets also need to be represented is an open question, the answer to which depends on the use to which the SVG map file will be put. I have opted not to include streets by default, to reduce SVG file complexity (SVGs with many elements take longer to render in browsers or other viewing programs), but you can override that default by passing true to the saveSVG() function.

The demo

You can try out the generator for yourself:

https://dnd.obormot.net/lacc/

Note that there’s no GUI. To generate a new map, simply reload the page. To save the generated map, open the JavaScript console and run the saveSVG() function. (Pass true to said function if you want streets to be included as distinct elements in the SVG; by default, only monoliths will be included, with streets left implicit as the negative space between monoliths.)

The code

Download the code (zip file). (Everything in the package is MIT licensed.)