(Previously: BigVTT project update #1: data format considerations)

The first of the requirements for BigVTT—indeed, the motivation for the entire project—is “large map support”. We’ve already established that we’ll be basing our map file format on Scalable Vector Graphics (SVG), which should allow us to support maps of arbitrary size¹; and it should be simple enough to design BigVTT’s UI so as to support any dimensions and scale for the battle grid, map image, etc.

But is that enough? Does “large map support” consist merely, literally, and simply, of allowing maps of any size?

Perusing the brief reviews of existing VTT software shows pretty clearly that the answer is “no”. Said reviews are full of comments like these:

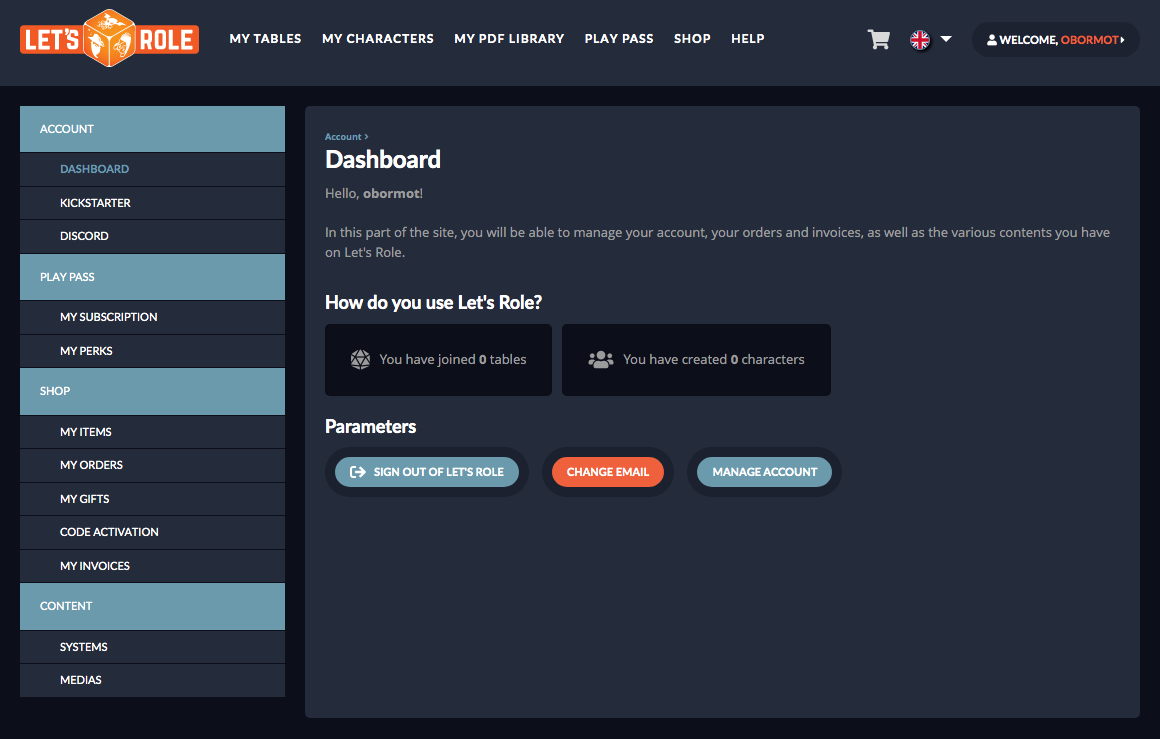
For one thing, the zoom function only goes down to 10%. But 10% of 851,200px is 85,120px. Who has a display that big? I certainly don’t. Being able to view, at most, 2% of the map on the screen at any given time is, obviously, horribly unwieldy, to the point where doing anything useful with such a map is impossible. There’s also no way to quickly move the view between distant parts of the map.

Large map sizes can be set, but then you can’t zoom in far enough to even see the individual grid squares, much less make any kind of use them by placing tokens or what have you.

Can’t zoom out to further than 50%.

I might be tempted to try using a statically upscaled map (despite the egregious file size required by this)… except that it is in any case impossible to zoom out to see the whole map of this size, and there are (as usual) no affordances for working with maps this large. (There is not even a zoom level indicator!)

And so on, and so forth.

In short, the mere ability to set a very large map size is not enough—the range of possible map sizes has to be integrated, in conceptual and interactional terms, into the design of the VTT, in a comprehensive way. To put it another way, there must be a robust set of affordances for working with very large maps. (And, of course, we will have to pay careful attention to ensure that we haven’t made it harder to work with maps of more ordinary sizes, either.)

Let us now examine in detail some specific program features and design considerations that are implied by this principle.

Zooming

This is a big one.

Zoom is a feature common to a wide variety of applications and tools, from page layout programs to CAD software to bioinformatics visualization packages to mapping/navigation tools. As a basic concept, it’s simple enough. We would like:

1. the ability to see our entire document (or data set or whatever is the entirety of the thing that we’re working on) on the screen at once, as a “high-level overview”
2. the ability to examine our data or object(s) at the lowest level, at a visual scale sufficient to both clearly see and effectively interact with every data element that has any meaning in the system
3. the ability to adjust the visual scale freely, switching between the above two scales, as well as any intermediate scale that may meaningfully be specified

The range of contexts in which these basic requirements apply is vast. We can add other desiderata, of course—but if you don’t have at least these three things, then you don’t have a zoom feature.

Zoom range

Translating the above to the specific context of a VTT, we want to be able to:

1. zoom out far enough to see the whole map on the screen at once
2. zoom in at least far enough to see tokens on the screen at full image scale
   • we may wish to be able to zoom in somewhat further than that, depending on, e.g., whether the VTT also provides map editing features, whether the VTT features “map objects” on a sub-grid-square scale, etc.
3. freely adjust the zoom level between the above two extremes

These, again, are the very basics—the fundamental motivations for having a zoom feature in the first place. And yet, in a frankly shocking fraction of the VTT apps I reviewed, the zoom feature fails to provide even that core functionality!

So the first and most basic requirement for BigVTT’s zoom feature is simply that it should have a full zoom range. The minimum zoom level should be as small as needed to see the full map on the screen at once. The maximum zoom level should be… well, we can return to this question that when we design our map editing tools, and various other features; but for now, let’s say that it should be 200% (i.e., big enough to see tokens at full image scale—which would be 100%—and then double that, just in case).

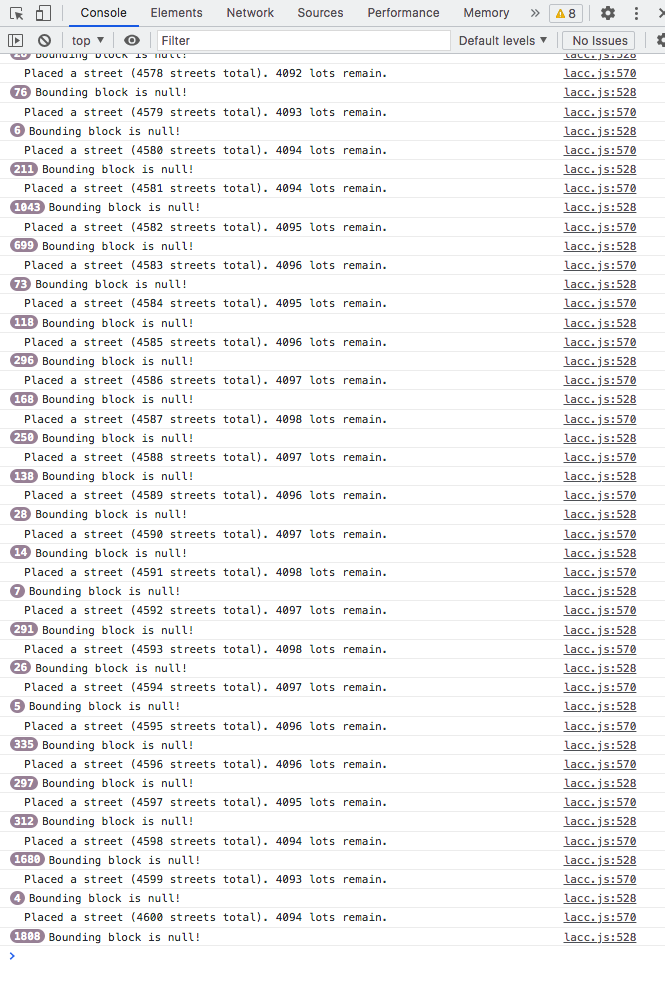
Let’s look at an example. On Roll20, the maximum zoom level is 250% (where “100%” means that the map will be displayed at a scale of 1 display pixel per map pixel, at whatever grid size in pixels is configured in the map settings; 70px per grid square is the default), and the minimum zoom is 10%; this is a zoom range of 25×.

Now, consider our example map for an arbitrary rectangular section of Lacc, the City of Monoliths. The map represents an area 12,160 × 9,820 grid squares in size. Let’s keep the maximum zoom level at 250%, and the grid scale at 70px per square. What would be the minimum zoom level, to fit the whole map in a 1216×982px viewport? That would be: 1216 ÷ (12,160 × 70) = ~0.00143, or ~0.143%. The total zoom range would thus be 250% ÷ 0.143% = ~1748×.

In other words, the zoom range of Roll20 is seventy times too small to properly support the use of a map this large. (Well, we might cut down the maximum zoom level from 250% to 200%, which gets us down to a mere fifty-six-fold mismatch. But a moment’s thought reveals that this is not actually an improvement, even a small one—after all, the minimum zoom level is unchanged! This is a good reminder that while the zoom range, as such, is a good proxy measure of what we’re aiming for, it is not actually identical to our desiderata for the zoom feature. The minimum and maximum zoom levels must independently match our requirements, and it does not suffice merely for the difference between them to be large enough.)

Some obvious design mistakes to avoid:

• setting the maximum zoom level to be some fixed multiple of the minimum zoom level (e.g., designating “the whole map is on the screen” to be “zoom level = 1”, and then setting the maximum permissible zoom level to be 10)
  • On large maps, this leads to not being able to zoom in far enough to see tokens
• the reverse of the above, i.e. setting the minimum zoom level to be some fixed fraction of the maximum zoom level (e.g., designating “the tokens are displayed at full image scale” to be “zoom level = 100%”, and then setting the minimum permissible zoom level to be 10%)
  • On large maps, this leads to not being able to zoom out far enough to see the whole map at once
• setting a minimum or maximum zoom level as a function of map scale (e.g., setting the minimum zoom level to “10% of intrinsic image scale”, or the maximum zoom level to “200% of intrinsic image scale”)
  • When using a map image with a large intrinsic size—which may be either very large bitmaps, or, more likely, SVGs with the values scaled to a large intrinsic size—this leads to not being able to zoom out far enough to see the whole map at once; conversely, when using a map image with a small intrinsic size, this leads to not being able to zoom in far enough to see the tokens
• setting a minimum or maximum zoom level as a function of grid scale (e.g., setting the minimum zoom level such that the display scale is 1 pixel per grid square)
  • On large maps, this leads to not being able to zoom out far enough to see the whole map at once

Note that while keeping these sorts of specific failure modes in mind is always a good idea, this entire class of mistakes can be avoided by regularly and thoroughly testing the zoom feature (along with every other feature, of course) with maps of various sizes (up to as large a size as possible).

Testing aside, we can also notice that most (though not quite all) of the mistakes listed above stem from a fundamentally bitmap-oriented approach. We will surely be less tempted to make a mistake like “the maximum zoom level is 2× the intrinsic image scale” if we’re using vector graphics, for which the intrinsic scale is an essentially arbitrary choice, which is made for convenience and does not correspond to any fundamental properties of the represented image data. (We will revisit the topic of image scale pitfalls when we discuss map image scaling, later in this post.)

Zoom UI

How—that is, by means of what specific interactions—should the user actually be able to zoom the map?

Once again, Roll20 is an instructive example. There are several ways to adjust the map zoom level:

• while holding down the Option (Alt) key, scroll the mouse wheel up/down (or use the scroll gesture on a trackpad, etc.)
• hit the ‘+’/‘−’ keys
• drag the zoom slider up/down
• click the zoom level indicator and select one of the options from the resulting submenu (“Zoom In”, “Zoom Out”, “Zoom to Fit”, “Zoom to 10%”, “Zoom to 50%”, etc.)
• click the zoom level indicator and type a number into the numerical text field

This is pretty good! Multiple different ways to do the same operation, various specific options, support for both keyboard-based and mouse-based interaction—all fine. The only problem is that “while holding down the Option key” requirement. Now, on Roll20, which is designed for relatively small maps (at least, compared to BigVTT), and where zooming is much less of a big deal, this may be fine; but on BigVTT, it simply won’t do. Moving the user view around the map must be as seamless an operation as possible.

Is there some reason not to let the user use the mouse wheel (or zoom gesture) to zoom the map at any time, without having to hold down any modifier keys? Sometimes, yes! (We will examine this in detail when discussing the design of the drawing tools, for instance; that’ll be a later post.) But usually—no.

So the second requirement for BigVTT’s zoom feature is that it should be as low-friction an operation as possible. Ideally, the user should never, even for a moment, have to think about how to zoom the map—it should simply feel like a perfectly intuitive form of “direct manipulation”. (Needless to say, we will also add multiple different ways to zoom the map, similar to how Roll20 does it. But the highest implementation priority will be given to those parts of the zoom functionality which allow for frictionless, seamless, continuous zooming, via simple mouse/trackpad gestures and single-key commands.)

Zoom display

This one’s pretty basic: there should be a UI element that shows the current zoom level. (Hardly even worth mentioning, right? And yet: so many VTTs fail even on this basic point!)

Zoom origin correctness

This is a fairly subtle point, and easy to get wrong—but if we don’t get it right (and most VTTs don’t), then BigVTT’s zoom functionality will feel clunky, and will be objectively less effective (i.e., will take more user actions and more time to achieve a desired result).

Consider the following map, with five areas, labeled A through E:

Let’s call this zoom level 1.0 (not 1%, or 100%, but 1.0; we decline to specify how this zoom level relates to the map scale—we will simply refer to zoom levels by how much more or less zoomed in they are, relative to this zoom level of 1.0). We are looking at the whole map, displayed in its entirety in our viewport.

Now suppose that we want to take a closer look at area A. If we zoom in, here’s what we’ll see at a zoom level of 2:

And at zoom level of 3:

We’ve got a close-up of C, but what we wanted was a close-up of A! We could certainly pan over to A:

Er… whoops. Didn’t quite pan in the right direction there… that does happen sometimes when you can’t see where you’re going! Ok, let’s adjust:

There we go. We’ve got our close-up of A, but it seems like we had to take an unnecessarily indirect path to get there. And what if we have to zoom in further than just a factor of 3? We’ll be doing a lot of zooming and panning, zooming and panning…

This sort of interaction gets awkward and annoying very quickly. (It’s exacerbated by the poor implementation of the pan function in many VTTs. For that matter, some VTTs—incredibly—don’t even have a pan function! Of course, BigVTT will support panning, and we will approach the design of the pan function with the same care that we’re giving the zoom function—but even so, this awkward two-step of zoom-and-pan is decidedly sub-optimal.) Surely there’s a better way?

The problem here, to be precise, is a fixed zoom origin. In geometric terms, if we consider the zoom operation to be a transformation of the image, the problem is that the origin of the coordinate system in which the transformation is applied is fixed (usually—as in our example above—to the center of the viewport).

But there’s no reason to maintain this invariant. We can locate the zoom origin anywhere we like. One obvious approach (used, for example, in the image-focus.js library) is to place the zoom origin at the location of the mouse pointer, when using the scroll wheel / gesture to zoom in or out.

Thus, returning to our example above, we’ve got our zoomed-out map:

• A
• B
• C
• D
• E

Now, with our mouse pointer in the vicinity of A, we scroll to zoom in. Zoom level 2:

• A
• B
• C
• D
• E

Zoom level 3:

• A
• B
• C
• D
• E

Much better. (Some small adjustment via panning may still be needed—but, importantly, we will no longer see the thing that we want to zoom in on move entirely off the screen as we’re zooming. When working with zoom ranges of 100× or greater, this makes a tremendous difference in usability.)

Panning

Just as important as zoom, for moving around a large map, is the pan tool. Incredibly, some VTTs do not even have a pan tool or pan function at all (I truly cannot fathom what their developers could possibly be thinking); but even those VTTs that do implement panning tend to do it imperfectly. Let’s once again consider Roll20 as an example, which (as usual) is one of the best in the category, and allows panning via the following methods:

• select the pan tool (‘a’ hotkey), then click and drag anywhere on the map
• use the mouse wheel to scroll up/down (without the Option key held down) to pan up/down only (this method does not permit left/right panning)
• on a trackpad, use the scroll gesture to scroll in any direction
• middle-click and drag anywhere on the map

Once again, this is pretty good! In fact, if you’re using a trackpad, I’d say that this implementation is already perfect. But what about mouse users? Surely, VTT use is correlated with the use of large displays, which in turn is correlated with the use of desktop computers, which in turn is correlated with the use of mice. (And, anyway, I use a mouse with a desktop workstation, so that’s the important use case to support regardless of what anyone else uses.) Not everyone’s mouse has a middle button (on mice with a clickable scroll wheel, such as the venerable—and excellent—Logitech M510, depressing the scroll wheel acts as a middle-click; but scroll-wheel-clicking-and-dragging is also awkward-feeling and less convenient than it should be). And, needless to say, “switch to a whole different tool (i.e., a different mode) to pan the map, then switch back to what you were doing” is terrible for maintaining a smooth, efficient workflow.

Here (and in many other cases, as we’ll come to see) we can look to vector drawing applications (e.g., Inkscape) for inspiration. Such programs have a simple solution to implementing efficient pan functionality: make normal mouse movement (without any mouse buttons held down) pan the view so long as the spacebar is held down. We will adopt this method without modification.

But we needn’t stop there. One sort of UI interaction which is common to both web browsers and computer games of various sorts is the use of the arrow keys to pan the view. Roll20 does not have this functionality (nor do many VTTs), but is there any reason for BigVTT not to allow this? There is not.

(This is an instance of a general UX design principle: if there’s an obvious and/or familiar way to do something, and letting the user do that thing doesn’t interfere with any other UI functionality, then let the user do that thing. Why not, after all? The upside is that your UI will be easier to learn and more pleasant and efficient to use. The downside is… nothing, really. The only real reason not to implement such things as “let the user pan the view with the arrow keys” is laziness—or, if you want to cloak your failures in a veneer of respectability, “resource constraints”.)

Minimap

The minimap is a UI element well-known to players of a variety of genres of video games, including real-time strategy games like StarCraft:

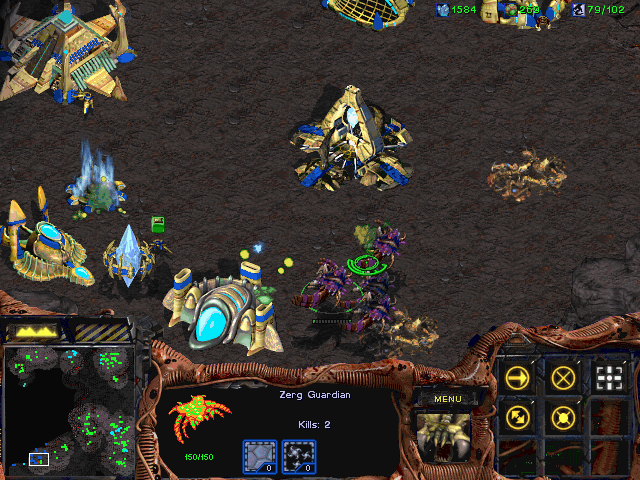
Figure 1. (Click to enlarge.) Minimap at the lower left.

MMORPGs like World of Warcraft:

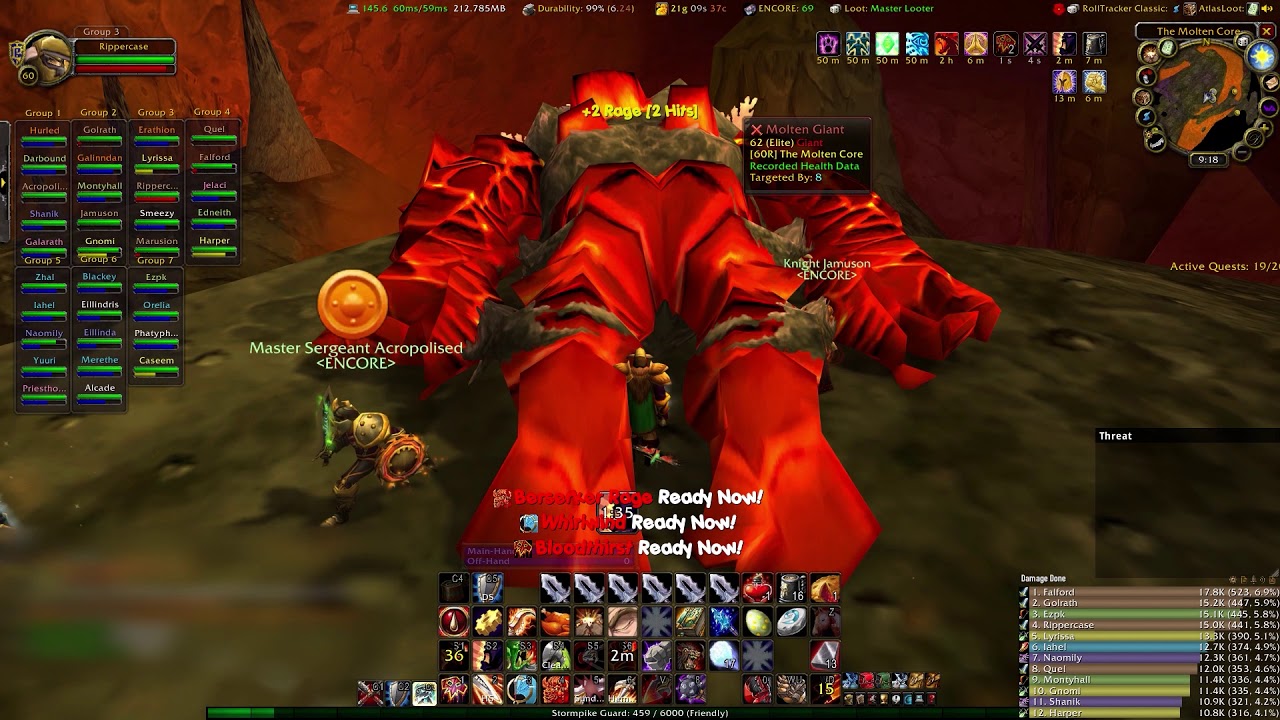
Figure 2. (Click to enlarge.) Minimap at the upper right.

Top-down space shooters like Escape Velocity: Override:

Figure 3. (Click to enlarge.) Minimap at the upper right.

First-person shooters like S.T.A.L.K.E.R.: Shadow of Chernobyl:

Figure 4. (Click to enlarge.) Minimap at the upper left.

The minimap has even started showing up in code editors, like Visual Studio Code:

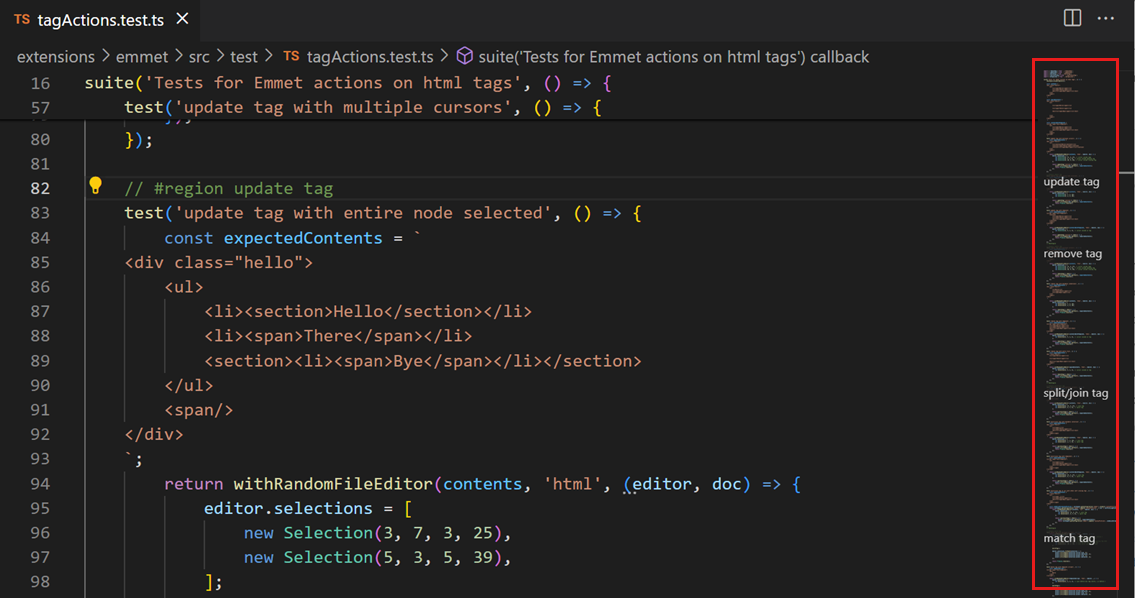
Figure 5. (Click to enlarge.) Minimap highlighted at the right.

And Sublime Text:

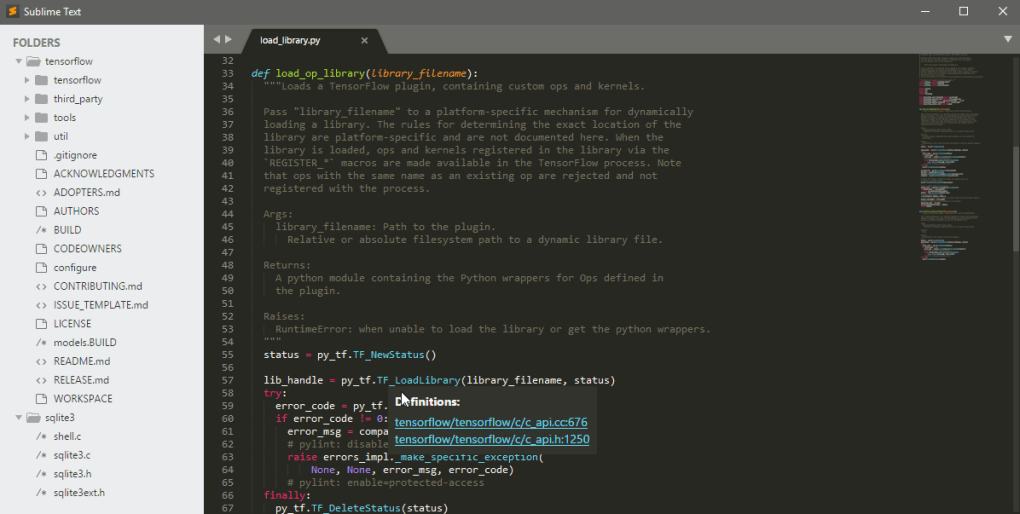
Figure 6. (Click to enlarge.) Minimap at the right.

But I have not seen even a single VTT implement such a feature.

And yet it seems like such an obvious thing, doesn’t it? The concept is simple: show, in a small window or panel (positioned in a corner of the screen, and hideable by the user), a scaled-down version of the map. If the main view is zoomed in so that it shows less than the whole map, show a rectangular indicator on the minimap, outlining the part of the minimap which corresponds to that portion of the map which is currently visible in the main view. This will dramatically improve the user’s ability to orient himself and to navigate the map. Make the minimap clickable, and you’ve also got a quick way to jump to anywhere on the main map (much quicker than panning, or zooming out and then zooming back in to a different part of the map).

However, there are some nasty traps and subtleties lurking in this fairly simple concept.

What is a minimap, anyway?

First, if we take a closer look at the four examples above (figures 1 through 4) of minimaps in games, we can see that we’re actually dealing with two related, but distinct, concepts. On the one hand, we’ve got the minimap as used in StarCraft (and WarCraft III, and many other real-time strategy games): a scaled-down version of the entire game map, which at all times shows 100% of the accessible game world (in that particular mission or game), and never scrolls, pans, zooms, or in any way alters the mapping from minimap display pixels to map coordinates. A minimap of this sort also incorporates “fog of war” functionality (such that parts of the map which have not been “revealed” to the player in the main view are also “blacked out” on the minimap). (We will discuss the fog of war in much more detail in a later post.)

The other three game minimaps we looked at (in World of Warcraft, Escape Velocity: Override, and S.T.A.L.K.E.R.: Shadow of Chernobyl) do not show the entire map. Rather, they show a portion of the map, in an area of some constant (though possibly adjustable) size, centered on the position of the player (and thus which part of the overall game map is shown on the minimap is something which is constantly updating as the player avatar moves around in the game world). Such minimaps usually do not incorporate any fog of war functionality. (In many such games—including World of Warcraft and S.T.A.L.K.E.R.: Shadow of Chernobyl—there is also a separate “view map” function, which temporarily replaces the normal player view with a full-screen view of the entire map. In Escape Velocity: Override, it would, of course, be pointless to show “the entire map”, i.e. the entirety of the accessible star system—it would be overwhelmingly empty space—and the “view map” function there instead shows the galaxy map, with the current star system that the player is located in indicated thereon.)

We may observe that the latter three games share the property that there is a single, uniquely defined “player position” (which corresponds to the player character in World of Warcraft and S.T.A.L.K.E.R.: Shadow of Chernobyl, and to the player character’s ship in Escape Velocity: Override), and the primary game view always shows the game world from that position (while it may be possible to rotate, zoom, or otherwise reposition the camera, the player is not permitted to move the view to some position where the player avatar—whether person or ship—is not). Meanwhile, in StarCraft (and in similar RTS games), there is no single “player position” (the player controls various units, buildings, etc., which may be dispersed across the whole of the map), and the primary game view may be repositioned with respect to the map, independently of the location of any player-controlled units (although that view may hide non-allied units, or may show nothing at all, depending on whether the player has explored that location or has vision there).

It seems intuitively obvious that a VTT much more closely resembles the latter category of game than the former: there is no single unique “player position” (one might be tempted to point out that a player in a TTRPG usually controls a single player character, but that is a misleading coincidence—consider what happens if the character conjures a summoned creature, for example… to say nothing of the DM, who will routinely control arbitrary numbers of tokens), and there is no reason why we shouldn’t let the player pan the map view independently of the location of any player-controlled tokens. (The fact that we have definite plans to implement a fog of war feature is another hint—though only a hint!—that what we want is an RTS-game-style minimap, and not the other sort.)

Scaling problems

So, question answered, right? We’ll have a minimap of the sort used in real-time strategy games: the entire map shown at once, a rectangular indicator showing what part of the map is currently visible in the main view, etc.

Not so fast! Let’s take another look at that StarCraft screenshot:

Figure 7. (Click to enlarge.)

We can see, in the lower-left-hand corner of the minimap, the one-pixel-thick rectangular white outline which acts to indicate which part of the map is currently visible on the screen. We should be able to use this to calculate how big, in screen pixels, the entire map is (in other words, how large a display would we need, if we wanted to see the whole map in the main view at once, without needing to scroll). Now, given how StarCraft renders the game world, and the design of the game UI, measuring the vertical dimensions here would be tricky and error-prone… but measuring horizontally should be unproblematic. So:

• the game window is 640px wide
• the minimap is 128px wide (exactly one-fifth as wide as the screen)
• the map position indicator on the minimap is 20px wide

Therefore the main game view is currently showing 20px ÷ 128px = 0.15625 of the whole map; therefore the entire map used in the screenshot is 640px ÷ 0.15625 = 4096px wide. (So, with a monitor like this one, you could see this entire map without having to scroll—horizontally, at least.)

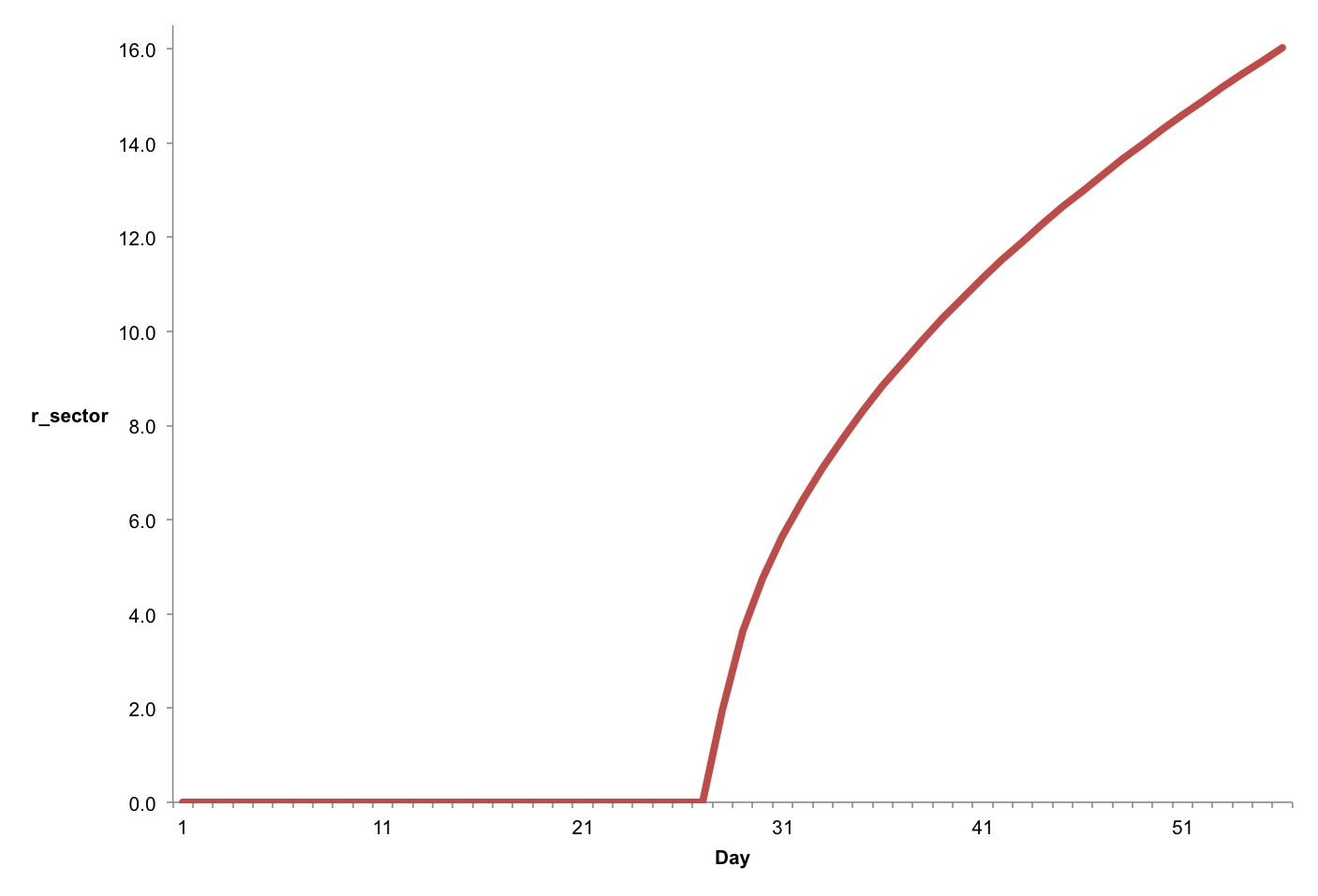
Now consider again our example map, which is 12,160 grid squares wide. Suppose that we render it at standard Roll20 grid scale (70 pixels to the grid square), and zoom in to our maximum permissible zoom level (200%, as we said earlier). The full map would thus be 2 × 70px × 12,160 = 1,702,400px wide. Let’s suppose that we are viewing this map on a standard 1080p display, in a full-screen viewport; thus the main map view will be 1920px wide. We’ll once again make the minimap one-fifth as large as the screen, i.e. 384px wide. Thus, the main map view in this case shows 1,920px ÷ 1,702,400px = ~0.0011278 of the map. Correspondingly, the rectangular indicator on the minimap (which shows which part of the map is currently visible in the main view) would have to be 0.0011278 × 384px = ~0.433px wide.

Hmm. That seems… less than useful.

It’s clear that a straightforwardly StarCraft-esque minimap implementation would not even be approximately or almost correct for cases like this; and it’s just as clear that no small adjustments to any of the numbers involved (e.g., “use smaller grid squares”) would fix the problem (because a small adjustment to some other number, in the opposite direction—e.g., an increase in the map size, or using a smaller viewport—would undo the fix). What we need is a principled approach which works well (as opposed to “almost kinda works ok-ish”) in “extreme” cases like this—after all, those are the very cases which motivated the design of BigVTT in the first place! Our solution, whatever it is, should not break down even under quite substantial shifts in map size, screen size, grid scale, etc.

So, how to do it? Let’s start by listing some assumptions and defining some boundary conditions. First, how big should the minimap display be, in terms of screen (or viewport) space? In the game examples that we looked at, above, the minimap ranges from being 9% as wide as the screen (in the World of Warcraft screenshot) to being 20% as wide as the screen (in the StarCraft screenshot). Our minimap will be easily hideable, and we will additionally try to have as little of the screen as possible taken up by UI elements; so we can be somewhat liberal in how much of the screen we devote to the minimap display. Still, too big would be bad (if it’s too big, the user will find the minimap obtrusive, and will prefer to hide it most of the time—which will reduce its value as a usability enhancement). Let’s pick 25% as our provisional value—our minimap will be no larger than one-quarter the width (and height) of the viewport.

Second, how small may the map position indicator on the minimap get before it’s too small to be useful? The indicator in the StarCraft screenshot is 20×12px large, but that would probably be too small for BigVTT—screens are both bigger and sharper (i.e., have a higher pixel density) these days, and we would not want to make BigVTT unduly difficult to use for users whose vision is not as perfect as it used to be. Let’s be conservative here, and double the width—we will say that the map position indicator should be no smaller than 40px wide.

What does that get us in terms of map size? With a 1920px-wide viewport, our minimap will be 480px wide; a 40px-wide map position indicator would thus mean that 40px ÷ 480px = ~0.083 or 1⁄12 of the map is currently visible in the main map view; and therefore, that our full map is 1920px × 12 = 23,040px wide. This is well short of the 1,702,400px width that our example map takes up at the maximum zoom level of 200% (we’re almost two full orders of magnitude short of the target). (Assuming the same map size in grid squares, a 23,040px total display width would mean that we are viewing the map at a zoom level of 2.7%, or ~1.9px per grid square.)

What to do? We’ve already established that we can’t adjust any of the key numbers on which this calculation depends (not in a direction that would help us, anyway). The only solution is to make a significant change to the way that the minimap functions.

Hybrid vigor

There are several possible modifications we can make to the minimap feature that would solve our problem, but here’s a fairly straightforward one. We will use a hybrid design: BigVTT’s minimap will be, essentially, a mix of the StarCraft-style “show the whole map at once” minimap and the World of Warcraft-style “show the player’s immediate surroundings” minimap.

To begin with, when the main map view is fully zoomed out, the minimap will show the entire map. (And the map position indicator will, of course, be as large as the entire minimap.) As the user zooms in, the map position indicator will shrink, until it reaches its minimum permissible size… at which point the minimap will also “zoom in”, dropping down to show not the entire map but only a fraction of it (with the map position indicator correspondingly resetting to a larger size). Zoom in further, and this process will continue, with the minimap showing a smaller and smaller (but still, always, larger than the viewport) portion of the whole map, each time a “zoom threshold” (i.e., a zoom level at which the minimap indicator has reached its minimum permissible size) is crossed. (The same process will work in reverse when zooming out, of course, until the minimap once again shows the entire map.)

In other words, at any given time, the minimap will show more of the map than the main map view does (except at the minimum zoom level, when the minimap and the main view both show the entire map). But the minimap will never show so much of the map that the map position indicator would be smaller than its minimum allowed size.

This will accomplish the goal of improving navigability and making it easier for the user to orient himself on the map, while robustly solving the scale problem, in a way that will never break, no matter how great the zoom range of any given map might be.

(There is another possible approach: showing multiple minimaps. That is: at minimum zoom level, we would show just the one minimap. When the user zooms in past the first zoom threshold—i.e., when the map position indicator would get smaller than its defined minimum size—we would spawn a second minimap, which would depict exactly the part of the map encompassed by the minimum-sized map position indicator on the first minimap. This process could continue indefinitely, spawning more and more minimaps. In practice, most maps and viewport sizes would result in perhaps three minimaps; even our example map, which is 12,160 grid squares across, would be fully handled with only four minimaps, at maximum zoom level. In any case, this approach, intriguing though it may be, will have to be left for a future version of BigVTT, as it is more complex to implement than the dynamically scaling minimap described above.)

View switching

A well-implemented zoom function, a useful minimap—these are things that benefit both the DM and the players, when using a VTT with a very large map. There are some features of the “large map affordances” type, however, which are primarily DM-oriented. One such feature is view switching.

Here we define a “view” simply as the combination of a zoom level and a position offset—in other words, some uniquely identifiable “viewport size and position” with respect to the map. So, for example, “viewing the entire map” is a view. “Viewing a region 5% of the map width wide, offset 31% from the top edge of the map and 12% from the left edge of the map” is also a view. In other words, zooming in or out changes the view; panning changes the view.

The question is: how do you transition from one view to another? Well, we just said it—zooming and/or panning, right? Now, suppose that you’re setting up the map (either during play or during prep), and you’ve got two locations of interest—let’s say, the part of the dungeon where the player characters are currently located, and some other area in the dungeon (where the PCs might soon go, perhaps). If you’re currently viewing one of these parts of the map, how do you switch to viewing the other part? You could pan over to it; or you could zoom out to where you can see both areas, then zoom in to a close view of the other area. (And, of course, the minimap will likely help you, in both cases.) But whichever method you use—suppose you have to switch back and forth, multiple times? Now continually zooming in and out, and/or panning (across, perhaps, a large stretch of the map), will introduce considerable friction into your workflow.

The solution to this is to have “view switching” functionality. This is not a single feature, but a cluster of related features, which all share the property that they involve “jumping” to some defined view with a single key command—without having to pan, zoom, minimap-click, or otherwise “manually” shift the main map view into the new position.

There are two basic categories of view switching features: built-in and user-definable.

Built-in view switching commands might include things like:

• “show full map”
• “go to location of last minimap ping”
• “go to location of the player character tokens” (repeated invocations might cycle between the PCs; or this command might show all the PC tokens on screen at once; or both)
• “go to location of the last-moved (or last-updated) token”
• “switch to previous view” (if the view was changed by some means other than simple zooming/panning)

User-defined view switching, on the other hand, may involve the ability to bind one of several shortcut keys (such as the numeric keys) to a specific view (or, perhaps, a specific token or group of tokens), and pressing the bound key would thereafter switch to that view (or to a view that shows that token or tokens).

As with the minimap, players of real-time strategy games will easily recognize this sort of feature. WarCraft III, for example, has the following view switching commands:

• Backspace to jump to your town hall (multiple presses to cycle between multiple town halls, if any)
• F8 to jump to an idle worker (multiple presses to cycle between multiple idle workers, if any)
• Spacebar to jump to location of last transmission
• F1–F3 (pressed twice) to jump to location of a Hero
• Numeric keys (pressed twice) to jump to location of a defined control group

The last one is, of course, an example of user-defined view switching; the other four are built-in view switching commands.

The long experience of RTS games pretty clearly demonstrates that a combination of built-in and user-defined view switching functionality vastly improves efficiency when navigating around a large map. This sort of feature is also fairly easy to build.

Map image scaling

This is actually two distinct, but closely related, questions: (a) what values are allowed / what variables are defined for determining map image scaling, and (b) what is the UI for controlling the values of those variables. (Even more so than view switching, questions of map image scaling almost exclusively concern the DM’s side of the table, since it’s the DM who sets up the map.)

Variables and values

What is “map image scaling”, anyway? Consider the following three variables²:

• the width of the map image, in either pixels (for an image in bitmap format) or arbitrary units (for a vector image)
• the width of a grid square, in image length units (pixels / units); a.k.a. “map scale”
  • equivalently, the width of one map length unit (e.g., 1 foot) in image length units (e.g., 1 pixel)
• the width of a grid square, in logical display pixels³; a.k.a. “grid scale”
  • equivalently, the width of one map length unit (e.g., 1 foot) in logical display pixels

The value of the first of these variables is a property of the image data, independent of any VTT functionality or even of any interpretation of the image. The second variable’s value arises from our interpretation of the image as a map that depicts some physical chunk of the game world. The third is a function of how we display the map on a screen. (Indeed, because we may display a battle grid without any map image at all, the third of these values does not even depend on there being a map image in the first place. Note that this third value is freely adjustable without altering either the image data or the mapping from the image data to the fictional reality which the image represents—this is what happens when we zoom the map view. However, we must still select a baseline grid display scale, which will correspond to a zoom level of 100%. This will allow us to create, import, and render bitmap assets—such as token graphics—in a way that will result in them looking good when displayed on screen.)

In order to usefully display and work with a map image, we need values for all three of these variables. We get the first value (width of the map image in image length units) from the image file—it has nothing to do with VTT functionality specifically. The second (width of a grid square in image length units) and third (width of a grid square in display pixels) are what we must specify—or, more precisely, what we must allow the user to specify, when importing a map image file and configuring a map.

(At this point it may seem like I am unduly belaboring a trivial technical point—making a mountain out of a molehill. The thing is, though, that in this part of a VTT’s design and implementation, it is very easy, via just a bit of carelessness or lack of thought, to make mistakes that, completely needlessly, dramatically reduce the usefulness and flexibility of the VTT app. I mention quite a few examples of such mistakes in my brief VTT reviews, and go into more detail on some selected examples later in this section. The point, in any case, is that thinking carefully and precisely about this aspect of the design will have outsized returns in how powerful a tool we end up building.)

Let’s take a look at some examples.

Example values

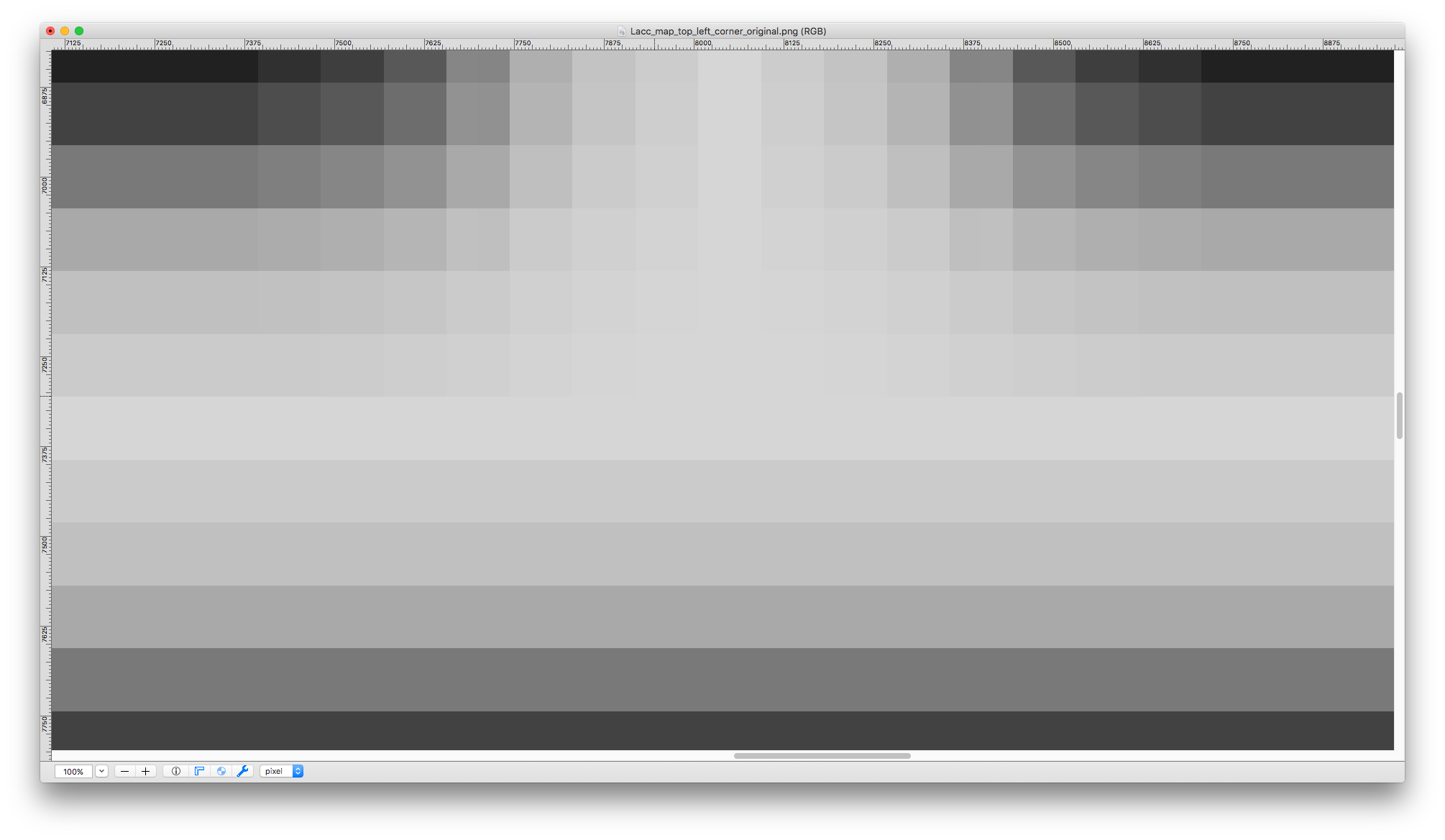
Figure 8. (Click to enlarge.)

Figure 8 shows a map of the fortress level of “The Sunless Citadel” (one of the most well-known and well-regarded Dungeons & Dragons adventure modules). The image file encodes a bitmap (JPEG) image 2008 pixels wide—that’s our map image width.

The map scale of this map can be determined by careful inspection and measurement, and turns out to be 36 pixels per grid square.

(It may occur to us at this point that as TTRPG maps, especially dungeon maps, often come with a grid already depicted in the map image, it should therefore be possible—perhaps not always, but often—to determine the map scale from the map image automatically. And, indeed, some VTTs, such as Shmeppy, do try to do this, with the use of computer vision algorithms. Note that determining pixels per drawn grid square is only half the battle, because not every map will be drawn at the same grid pitch—i.e., mapping of grid squares to game-world length units like feet—as the grid pitch preferred by the user for the purposes of using the image as a VTT map. For example, given a map image with a 10-ft-square grid, we will want to import the map at a map scale half of that which would be inferred from the image. Inferring the grid pitch used in the map from text labels in the map image may be something which is now doable automatically via the use of AI tools, but, to my knowledge, no VTT app has such a feature yet.)

The grid scale at which the map will be displayed is, of course, entirely up to the user. The choice of grid scale depends on several factors. We want the map image, and any character token graphics, to look good when rendered on the screen. When using bitmap-format map images, if the image has a great deal of detail, textures, etc., we therefore would like the grid scale to be not too much greater than the map scale—otherwise, image scaling will blur (if using interpolation) or pixelate (sans interpolation) the map image, ruining the carefully drawn detail and textures and so on. Similarly, if the character token art for our Medium-sized (i.e., 5-foot-wide token) characters is drawn to a 100px scale, they won’t look very good when scaled down to 30px. The choice of grid scale also affects usability: make it too big, and you won’t be able to fit (at 100% zoom) enough content on the screen at once to be useful (you can zoom out, of course—but we’d prefer the 100% zoom level to be usable in play); make it too small, and players won’t be able to see what’s going on (again, you can zoom in—but… etc.).

In practice, choice of grid scale isn’t a very hard problem. There is a relatively narrow range of grid scales which work well (approximately 40px per grid square on the low end to perhaps 120px per grid square on the high end). Within that range, selecting a value has more to do with standardization and familiarity than any hard technical constraints. We must be careful when making assumptions here, as we’ll see; but, for now, we can take as a sensible default the Roll20 default grid scale of 70px per grid square. Note, again, that the grid scale may be set independently of any specific map image, or in the absence of any map image at all (i.e., it is a property of how the battle grid is displayed, no matter what map image underlies it).

So, when importing an image file to use as a map image, the key number that the user will need to specify is the map scale. In our Sunless Citadel example above, the map scale, again, is 36px per grid square—or, at it happens, approximately one-half of the grid scale (in other words, at 100% zoom level, the image will need to be magnified by approximately 2× for display). Now, consider this question: what is, in general, the range of permissible values which this variable may take on?

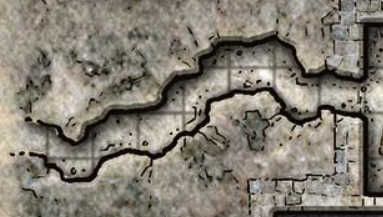
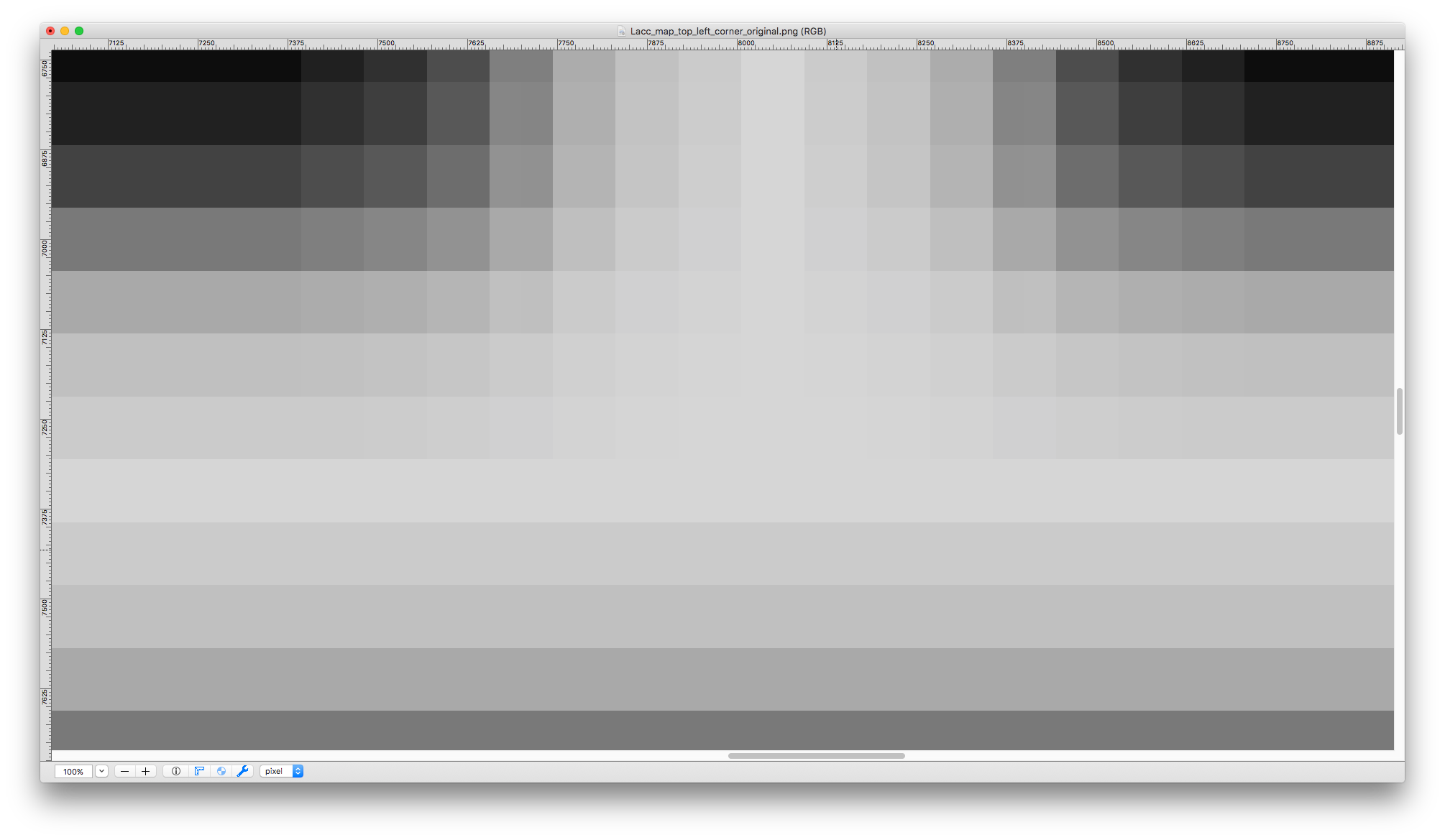
Can the map scale be larger than the grid scale? Certainly—here’s a map image drawn at 77px per grid square:

Figure 9. (Click to enlarge.)

And here’s one at 116px per grid square:

Figure 10. (Click to enlarge.)

Either map can be displayed at a 70px grid scale with no problems, of course.

What’s the upper limit? Should there be one? Well, if our map image is a bitmap, then as we increase the map scale, we’ll eventually find that either our map shows only a very small area (measured in grid squares), or else the file size is unmanageably large—or, even more eventually, both. But “eventually” is the key here; none of these problems are guaranteed to arise at a map scale of 100px per grid square, or 200px per grid square, or 300px per grid square.⁴

But recall that we’ve already decided on a vector format as the default for BigVTT map data (and even if we hadn’t, we’d certainly need to support a vector format as an option, else truly large maps would be impossible to create and use!). With a bitmap-format map image, the map scale is expressed in pixels per grid square—but there are no “pixels” in an SVG file, only abstract length units. Multiplying or dividing all coordinate values in an SVG file by 1000, or any other number, will make no difference to how the file is rendered, once it’s scaled to some display size. This means that, since the map scale of a vector-format map image is expressed in abstract length units per grid square, there cannot be any upper limit to the permissible map scale when importing a vector image file into BigVTT for use as a map image. A map scale of 10, or 100, or 1000, or 1 million length units per grid square—any of these should be permissible.

What about the lower limit? It’s clear enough that the same reasoning applies to vector image files as for the upper limit of map scale—there should be no lower limit at all. A map scale of 1 length unit per grid square is perfectly possible, or 0.1, or 0.01, etc. This suffices to answer the question, but note that the same is true even if we’re using a bitmap image file—there’s simply no reason to assume that a single pixel in the map image cannot represent an entire grid square, or even multiple grid squares (as we have seen). High-resolution map images are certainly common, but should not be required.

In summary, the map scale at which a map image file is used in BigVTT should be allowed to take on any positive value from arbitrarily small fractions to arbitrary large numbers. The only constraints should be those which are necessary to avoid integer overflow or similar technical problems.

The next question, then, is how the user can specify this value (or, to recall the caveat here, values—one each for the horizontal and vertical axes, as map images may not always be drawn with a precisely square grid).

Map scaling UI

There is a right way to implement a VTT’s map scaling UI, which easily and automatically avoids problems. And then there is a wrong way, which causes problems for no good reason. Needless to say, most VTT developers choose the latter.

The right way is the way that Roll20 does it:

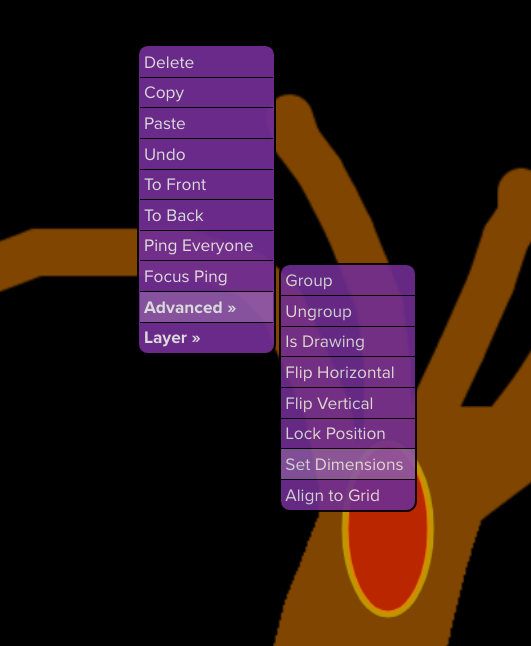
Figure 14. (Click to enlarge.)

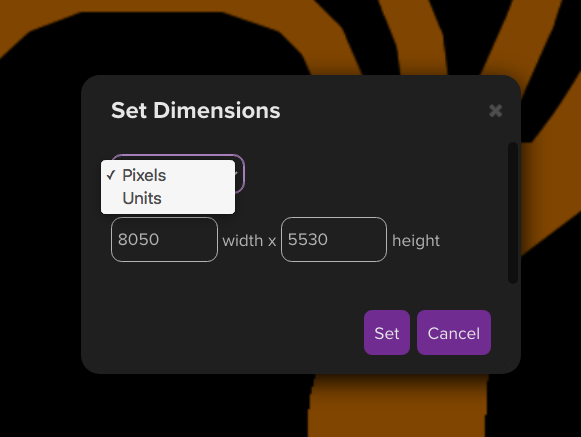
Figure 15. (Click to enlarge.)

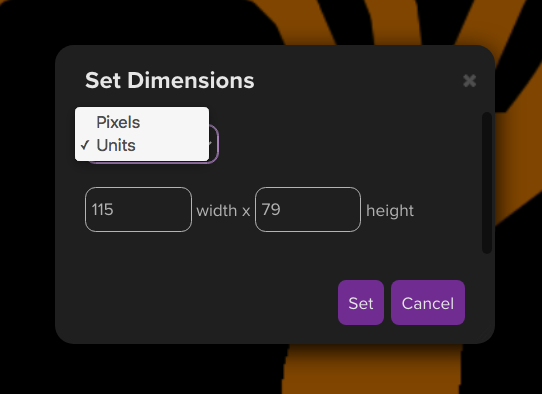
Figure 16. (Click to enlarge.)

Simply let the user specify, in either grid squares or pixels, what size (width and height, independently) the map image should be scaled to.

The minimum value for both width and height is 1. (Obviously the map image can’t be drawn at less than 1 pixel in width or height.) The maximum is unbounded (or bounded only by technical constraints). Setting these values correctly automatically results in the map scale being whatever it should be, without the developer or the user having to think about “map scale” in explicit terms.

(Roll20 also has a “drag-the-selection-handles” feature, like you might find in any vector drawing program. This, too, is a no-brainer feature.)

This, on the other hand, is pointlessly wrong:

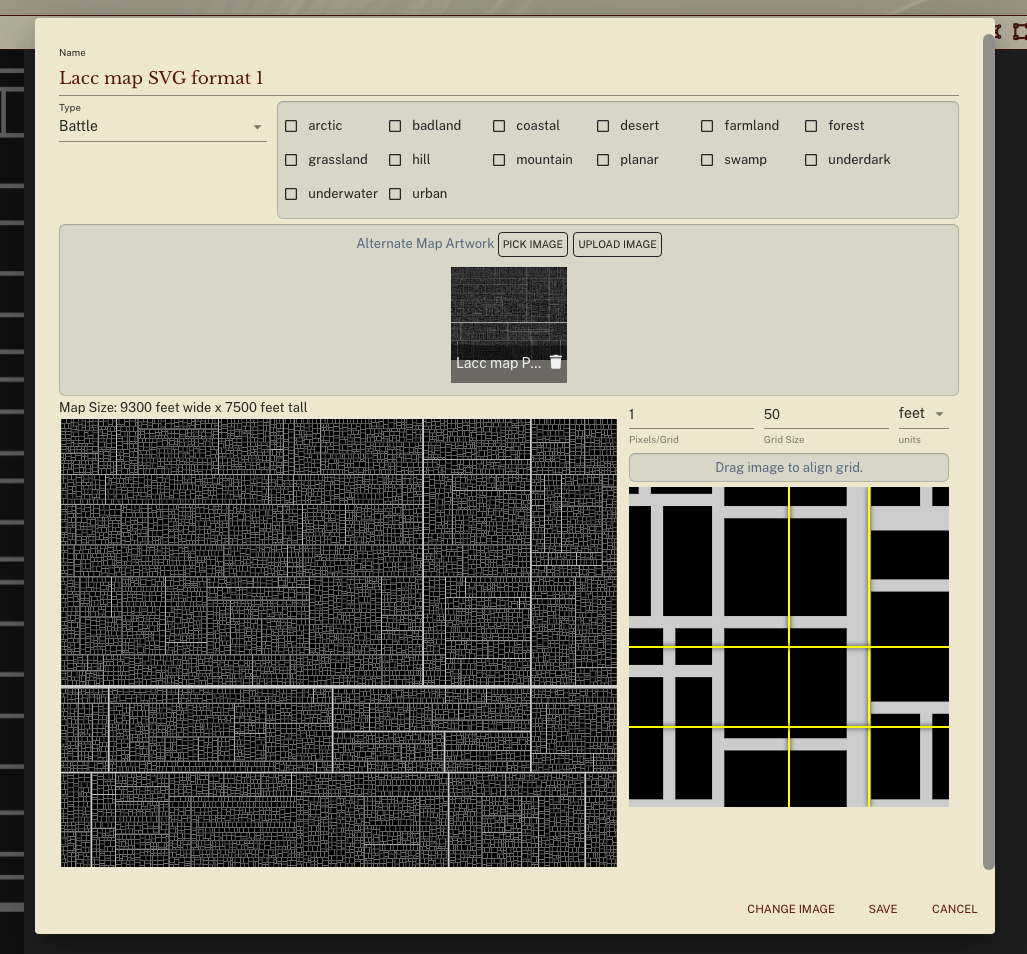
Figure 17. (Click to enlarge.)

Shard Tabletop lets you set a map scale, but the input field prevents you from entering a number lower than 1 or higher than… 370 (for some reason). This is an absolutely unnecessary limitation that simply does not arise with a Roll20-style map scaling UI.

This is extremely wrong:

Figure 18. (Click to enlarge.)

Alchemy RPG features a slider to set map scale, which does not even show you the number that the slider position corresponds to (!), and the lower bound seems to be something like 135px (!!) per grid square. Just execrable UX design.

Another common pitfall which many VTTs stumble into is allowing the map image to be rescaled—but only via dragging, with no option to specify the width and height precisely via numeric input fields. I can only assume this is due to developer laziness, since the disadvantages caused by this oversight are extremely obvious.

Anyway, as I said, the correct design here is very easy: simply copy what Roll20 does, the end.

Interpolation

We have previously discussed the pitfalls of interpolation algorithms used in image scaling, and their consequences for the usability of bitmap-format map images at low map scales. Now, the principled solution here is one which we’ve already selected—namely, using a vector image format for our maps. However, if it is not unduly difficult, it would be better to also allow for the use of bitmap-format low-map-scale map images. The key question here is whether we can efficiently resize bitmap images without interpolation.

The answer is yes! The CSS property image-rendering: pixelated does what we want for <img> elements, and the imageSmoothingEnabled property does the trick when scaling image data in a <canvas> element. Both are widely supported.

What’s next?

Upcoming posts will discuss fog of war features, action history, BigVTT’s rendering system, and more.

1 We may run into hard-coded limitations imposed by web browsers, such as a maximum layout size of a document, or some such thing. And, even before we hit such limits, we will quite likely be constrained by the hardware on which BigVTT is run (both RAM limits and CPU/GPU performance difficulties may come into play here), though of course we will do our best to optimize the code to make efficient use of resources. Such things cannot be avoided; the key thing here is to impose no artificial limitations, i.e. we should have no restrictions on map size that are consequences of nothing more than poor UI design (e.g. a map pixel ratio slider that only goes down to 1), or of short-sighted choices in implementation (e.g. hardcoded limit values that are well short of those required by the browser). ⇑

2 In each case these can vary separately for the horizontal and vertical dimensions, but because these are orthogonal to each other—literally—we need not concern ourselves much with their interaction; so we will simply talk of single scalar values in each case, and assume that adding the second dimension works in the obvious ways. Where this assumption doesn’t hold, we’ll note it explicitly. ⇑

3 What is a “logical display pixel”? Here we are not referring to image pixels (which, confusingly, are sometimes referred to as “logical pixels”). Rather, we are referring to what the link in the previous sentence calls “device-independent pixels”, or what this article calls “points”, or what in web development are often known as “CSS pixels”. (The last of those is particularly relevant to BigVTT, as it is a browser-based app.) ⇑

4 How large a map scale can we expect, in practice, to always result in unmanageably large bitmap map image files? (The question is meaningless for vector graphics, of course.) Well, that obviously depends on what “unmanageably” means, but let’s arbitrarily pick a file size (let’s say, 5 MB) and a map size in grid squares (let’s say, 20×20), and ask: how large can we make the map scale while still fitting a map of those dimensions into that file size?

The answer obviously depends on what the map depicts, and how. Technically, this is a 20×20 map, at a map scale of 1000px per grid square:

Figure 11. (Click to enlarge, although there’s nothing more to see at a larger size.)

Yes, it is an absolutely uniform block of a single color (white), 20000×20000px in size—with a file size of 108 KB.

That’s an extreme (we could even say “degenerate”) case, obviously, but the same principle applies to more mundane cases. This is a 20×20 map:

Figure 12. (Click to enlarge.)

And this is also a 20×20 map:

Figure 13. (Click to enlarge.)

The former is 355 KB in file size, with a map scale of 36px per grid square. The latter is 91 KB in file size, with a map scale of 132px per grid square. (Both are sections of real dungeons that I, personally, have used in games that I’ve run.)

So the answer is—well, probably nothing short of four digits, at least. ⇑

(Previously: Extreme D&D DIY: adventures in hypergeometry, procedural generation, and software development (part 3))

Choice of data format is critical in a project like this.

As noted in my last post, BigVTT will support map background images (as well as images for tokens, objects, etc.) in as many image file formats as permitted by the capabilities of modern browsers. PNG, JPEG, GIF, WebP—if the browser can handle it, then BigVTT should be able to do likewise.

However, the preferred map image format—and the format which will be used internally, at runtime, to represent the map and objects therein—will be SVG. There are several reasons for this, and we’ll discuss each one—but you can probably anticipate most of the advantages I’m about to list simply by recalling the acronym’s expansion: Scalable Vector Graphics.

Vector/bitmap asymmetry

Bitmap graphics and vector graphics are asymmetric in two ways:

1. A vector image file can contain bitmap data, but not vice-versa.
2. It is trivial to transform a vector image into a bitmap, but the reverse is much, much harder.

This fundamental asymmetry is, by itself, enough to tilt the scale very heavily in favor of using a vector file format as the basis for BigVTT’s implementation, even if there were no other advantages to doing so. (Indeed, the vector format would have to come with very large disadvantages to outweigh the asymmetry’s impact.)

Compared to what?

Let’s take a step back and ask: what exactly are the alternatives, here? That depends, of course, on what we need our data format to do; and that depends on the purpose to which it’s to be put.

For what purpose?

Well, what is this a data format for, exactly? And what do we mean to do with the data stored thus?

Map background image

The term “map” is used in multiple ways in the VTT space, so we’ll have to be careful with our language.

We can think of the totality of all the entities or “pieces” which make up the VTT’s representation of the game world as being arranged into layers.

This is necessarily a somewhat loose term. Many VTTs (e.g., Roll20) do indeed organize the content of a “scene” or “room” or “page” into “layers” (in Roll20’s case, for example, there are four: the map layer, the token layer, the GM layer, and the lighting layer), and these are often modeled, in one way or another, on the way that the concept of layers is used in vector drawing programs like Adobe Illustrator. (This is only natural; VTTs and drawing apps share many similarities of purpose, so UX design parallels are to be expected and, indeed, often desirable.) However, the way that the general concept of “layers” is instantiated varies from VTT app to VTT app (and some VTTs do not make use of layers in their design at all—to their detriment, I generally think), so we cannot rely on existing consistent, sharply drawn definitions of any of the terms and concepts we will need to use.

What I’m going to call the map background image is the “lowest” layer of the VTT’s representation. There is nothing “underneath” this layer (hence, it is necessarily opaque—has an alpha value of 100%, both in the visual sense and in any functional sense, if applicable—and either fully covers the entire mapped region or else relies on a guarantee that any gaps in this layer will be covered by specific other layers).

The content of the map background image, in terms of what it represents in the game world, depends on what sorts of things the VTT must represent and model.

For example, suppose that we are constructing a map for a dungeon. Should the map background image include the dungeon walls? Well, that depends on whether the VTT needs to model those walls in any way (e.g., to determine sight lines for fog-of-war reveal operations). In the simplest case, where the code does not need to know anything about the walls (because either there is no fog of war, or the DM will use the region reveal tools to manage the fog of war manually; and there are no token movement constraint features, etc.), the map background image layer can include the walls. Similar considerations apply to the question of whether the map background image should contain objects (such as furniture, statuary, water features, etc.), terrain elements (such as mountains), etc.

Is it better for the map background layer to be composed of a single bitmap image? Or multiple bitmaps (possibly embedded in a vector file format)? Or vector-graphical data exclusively? Does it make any difference at all?

An obvious answer might be that the map background image can just be a bitmap, because there’s no need for it to have any internal structure—in other words, it won’t contain any elements that need to be modeled. (Because any such elements would instead be contained in other, “higher” layers.) And storing a single background image, that depicts what is essentially 2D data, as a bitmap, is maximally easy.

On the other hand, there are two considerations that motivate the use of a vector format even in this case.

First, there’s the fact that vector graphics can be rendered well at any zoom level (that’s the “Scalable” part of “Scalable Vector Graphics”). This applies to map background images in particular in the form of patterns or textures; we can represent regions of the map via patterns/textures which are rendered in a scale-dependent way, rather than consisting merely of a static bitmap. This is an element of visual quality, and so at first may not seem to matter very much; but when pushing the bounds of what sorts of creations are possible (in the dimension of size, for instance, as we are doing here), what is unimportant at “ordinary” points in the distribution may become critical as we move up or down the scale. In other words: blow up a bitmapped map texture to 2x scale, and it is perhaps slightly blurry; blow it up to 200x scale, and it’s a either completely unusable mess, or a solid block of color, or something else that is no longer the thing that it should be.

But there is a second, and even more important, consideration: what if the very lowest layer of the representation nevertheless contains elements that should be modeled?

How might this happen? Well, suppose that we wish to know the terrain type of any given map region. (In a dungeon or indoor setting, this might be “floor type”.) And why would we want to know this? Because it might affect character movement rate across regions of the map.

Remember our list of requirements for BigVTT? One of them was “measurement tools”. What are we measuring? Certainly distance, if nothing else (perhaps other things like area, as well), but distance for what purpose? The two most common uses of distance measurements in D&D are (a) spell/attack ranges and (b) movement rates. When measuring distances for the purpose of calculating spell/attack ranges, there is no reason to care about terrain/floor type. But when measuring distances for the purpose of determining how far and where a character can move in any given unit of time/action, terrain considerations suddenly become very important!

Now, this doesn’t mean that we have to model terrain effects on every map we construct. But we certainly might wish to do so, in keeping with BigVTT’s design goals. And that means that either the lowest map layer will have to store region data (that is, some mapping from map coordinates to terrain metadata, the most obvious form of which is a set of geometrically defined regions—each with some metadata structures attached—which together tile the map), or else we will need to apply terrain region data as an out-of-band metadata layer on top of what is otherwise an undifferentiated (presumably bitmap-encoded) map background layer. These two approaches are essentially isomorphic; even if the visual representation of our map background image consists of some sort of bitmap data, either in one large chunk or sliced up into smaller chunks, nevertheless this layer as a whole should be capable of representing more structure than simply “a featureless grid of pixels”.

It should be noted at this point that it is possible to encode things like terrain effects (and other region metadata) in a bitmap format. After all, that’s what maps are. But programmatically extracting structured metadata from a bitmap is a much harder problem than parsing an already-structured data format. (Perhaps AI will change this, but for now the disparity remains.) And, of course, a structured format can store vastly more data than a bitmap, for the simple reason that there’s no limit to how much metadata can be contained in the former, whereas there are obvious information-theoretic limitations on what may be encoded in a bitmap (and pushing the boundaries of those limitations inevitably leads to a sharply increasing algorithmic complexity).

Fixed non-background features

Here we are referring to things like walls. (In outdoor maps, elements like cliffs, trees, etc. may also fall into this category.) These may be part of the map background image (see previous section) in a simple scenario where we don’t need to model lines of sight and constraints on token movement/position. However, as the feature list for BigVTT includes fog of war and similar functionality, we do need to be able to model this sort of thing; thus we’ll need to have some way of representing walls.

How should such things be stored and modeled? One way (used by Owlbear Rodeo, for instance) is to have a layer which acts as an alpha mask (a 1-bit mask, in Owlbear Rodeo’s case), and encodes only the specific functional properties of walls or other fixed features, while the visual representation of those features remains in the map background image. Another way, also an obvious one, is to have multiple bitmap layers (each with a 1-bit alpha mask attached); thus, e.g., layer 0 (the map background image layer) would contain the dungeon floor, while layer 1 (the fixed features layer) would contain the walls. (One interesting question: consider the spot on the map occupied by a wall in layer 1; what is at that spot in layer 0? It could be nothing—that is, a transparent gap—or it could be more dungeon floor. The former arrangement would result if we took an existing, single-layer, bitmap and sliced it up to extract the walls into a separate layer; the latter could—though not necessarily would—result if we drew the map in multiple layers to begin with. Note that these two approaches have different consequences in scenarios where fixed map features can change—see below.) And, of course, we can also store map features like this as objects (possibly with textures or bitmap background images attached) in some sort of vector or otherwise structured format.

Here a similar argument applies to that given in the previous section: we should store and model fixed non-background features in as flexible and powerful way as possible, because it allows us to properly represent and support a variety of tactical options in gameplay.

What do I mean by this? Well, consider this: can walls change?

Put that way, the answer is obvious: of course they can. A wall can simply be smashed through, for one thing (with mining tools, for instance, or adamantine weapons, or a maul of the titans). Spells like disintegrate or stone shape can be used to make a hole in a dungeon wall; passwall or phase door can be used to make passageways where none existed. And what about an ordinary door? That’s a wall when it’s closed, but an absence of wall when it’s open, right? (Of course you could say that doors—and windows, and similar apertures—should be modeled as stationary foreground features, as per the next section; but this is a fine line to walk, and in any case doesn’t account for the previous examples.)

It’s clear that (a) these scenarios all have implications for BigVTT functionality (fog of war / vision), and (b) we should ensure that such things are robustly modeled, so as to do nothing to discourage tactics of this sort (which make for some of the most fun parts of D&D gameplay). This means that walls and other fixed non-foreground features must be stored and modeled in a way that makes them easy to modify, and which allows us to represent the consequences of those modifications in no less correct and complete a way as we represent the un-modified map.

Stationary foreground objects

This is stuff like furniture, statuary, etc. It could (depending on implementation) also include things like doors (see previous section). In outdoor environments, trees could also be included in this layer; things like large boulders, likewise.

Stationary foreground objects may or may not obscure sight. They may or may not have implications for movement. (That is, it may or may not be possible to move through spaces occupied by such objects; if it is possible to move through them, they may or may not impose modifications to movement rates.)

This variability in how objects of this kind interact with movement and vision suggests, once again, that we must aim for a very flexible way of storing and modeling such things. (The emerging theme here is that our data format should do nothing, or as little as possible, to constrain our ability to model the various ways in which characters may interact with the various in-game entities represented by elements of the map. We should even strive to minimize any friction imposed on those interactions by our UI design—it should not only be possible, but easy, to represent with our map all the things that characters may do with the things that the map represents.)

It might be useful to consider one small concrete example of the sort of flexibility that we want. Suppose that the player characters are in a forest. How should we model the trees? Having them be fixed background features seems intuitively obvious (they certainly obscure vision, right?). But now suppose that one of the trees turns out to be a treant. We do not want the players to have any hint of the “tree”’s true nature until and unless it decides to make itself known, so certainly it should behave (in terms of the map representation) like any other tree. But when the treant begins to move, speak, attack, etc., it should behave like a token (see below). We do not want the DM to have to do anything tedious, annoying, or difficult to manage this transition.

(Think twice before you suggest any jury-rigged solutions! For example, suppose we say “ah, simply let the DM have a treant token prepared, either sitting in some hidden corner of the map or else stored, fully configured, in the token library [we assume such a feature to exist], to be placed on the map when the treant animates”. Fine, but what of the tree object? The DM must now delete it, no? Well, that’s not so onerous, is it? But what if there are multiple treants? Now the DM must place multiple tokens and delete multiple objects. Still not a problem? But now we enter combat, and the DM—spontaneously, in mid-combat—decides that the treant should use its animate trees ability to make two normal trees into treants—with selection of candidate trees being driven by tactical considerations, thus much less amenable to preparation. Suddenly the DM is spending non-trivial amounts of time messing around with tokens and objects, slowing down the pace of combat. Not good.)

Situations like this abound, once we think to look for them. A boulder might turn out to be a galeb duhr; a statue is actually an iron golem; an armoire is a mimic waiting to strike. This is to say nothing of magical illusions, mundane disguises, etc. Anything might turn out to be something else. And, of course, the simplest sort of scenario: an object (such as a statue), be it as mundane and naturally inert as you like, may simply be moved or destroyed!

It would be best if our map representation robustly supported this inherent changeability and indeterminacy by means of a flexible data model. As before, we do not have to model any of the things I’ve just described, on any given map for any given scenario. But we may very well wish to do so, without thereby exceeding the scope of BigVTT’s basic feature roadmap.

Disguised & hidden elements

This is really more of the same sort of thing as we’ve already mentioned, across the previous several categories, just made more explicit. Basically, we are talking about any variation of “it seems like one thing, but is a different thing”. This might include:

• creatures disguised as inanimate objects (or even as walls, floors, etc.)
• illusionary walls (or, more generally, parts of the environment that look like they are real things but actually aren’t)
• invisible walls (or statues or couches or anything)
• entire parts of the environment that look different from how they actually are (via something like the mirage arcana spell)
• secret doors
• concealed traps

But wait! What exactly is the difference—as far as VTT functionality goes—between “it’s one thing, but (due to disguises or magic or whatever) looks like some other thing”, and “it’s one thing, but then it transforms into another thing”? Don’t both of those things involve, at their core, a change of apparent state? A wall that can disappear and a wall that wasn’t there in the first place but only looked like it was—will we not represent them, on the map as displayed to the players, in essentially the same way?

This suggests that was we need to store and model is something as broad as “alternate states of elements within the map representation, and a way of switching between them”.

And, of course, it’s not just walls or other fixed elements that can change, be disguised, be hidden, or otherwise be other than what they at some other time appeared to be—it’s also creatures (see the next section), effects (the section after that), etc.

Mobile entities (tokens)

Unlike all of the elements we’ve discussed so far, which at least possibly might be represented by a simple, single-layered bitmap image (albeit with considerable sacrifices of flexibility and ability to represent various properties and aspects of the game world), there is no possibility whatever of having tokens be simply a part of that static format. The movability of tokens, and their separateness from the map, is inherent to even the most narrowly construed core of virtual tabletop functionality.

What kinds of things are tokens? Without (for now) thinking too deeply about it, let us give a possibly-incomplete extensional definition. Tokens can represent any of the following:

• player characters
• NPCs
• monsters
• creatures of any sort, really
• certain magical effects, constructs, or entities that behave like creatures in relevant ways (e.g. a spiritual weapon, a Mordenkainen’s sword, a Bigby’s grasping hand, etc.)
• illusionary effects that appear to be any of the above sorts of things (e.g. a major image of a dragon)
• vehicles?
  • (Here we are referring to chariots, motorcycles, and the like; we probably wouldn’t represent a sailing ship, say, as a token… or would we?)

It might occur to us that one way to intensionally describe the category of “things that would be represented as tokens” might be “anything that might have hit points and/or status effects”. (We might then think to add “… or anything that appears to be such a thing”, to account for e.g. illusions.) However, that definition leads us to a curious place: what about a door (or a platform, or a ladder, or a statue, etc.)? Doors have hit points! Should a door be a token? As noted in the previous section (with the treant example), an object can become a creature very quickly (a treant can animate a tree; or a spellcaster can cast animate objects on a door or statue), or an apparent object can turn out to have been a creature all along. (Likewise, a creature can become an object, with even greater ease. The most common means of doing so is, of course, death.)

Is there, after all, any difference between tokens and stationary foreground objects? Or is the line between them so blurred as to be nonexistent?

On the other hand, it seems like it would be annoying and countinterintuitive to, e.g., drag-select a bunch of (tokens representing) goblins, only to find that you’ve also selected miscellaneous trees, rocks, tables, etc., even if we’ve already decided to represent the latter sorts of things as independent objects in our model (and not just parts of the map background image). Some differentiation is required, clearly.

In any case, how should we store and model tokens? As already noted, they are inherently distinct from the map. So we’ll have to store them separately, as the least. We’ll thus also need to store token position, state, and similar data, no matter what data format we are using for the map. What about internal structure? What is a token? If nothing else, it’s a graphical element of some sort, plus a non-graphical identifier. The rest, we can think about in more detail later.

Effects & phenomena

Here we are referring to things like a wall of fire, a magical gateway (e.g. one created by a gate spell), an area affected by an entangle spell, and other things of this nature. Such things are not exactly physical objects or parts of the terrain / architecture, and they’re not exactly creatures or similar autonomous entities, but they definitely exist in the game world and affect, and can be interacted with, the player characters as they move around the mapped area. Effects & phenomena share many functional qualities with the sorts of things typically represented by tokens, and likewise share many functional qualities with the sorts of things that we might classify as “stationary foreground objects” or the like. (Indeed, there is considerable overlap: a wall of fire is an effect, but what about a wall of ice—isn’t that pretty much your regular wall? But what about the “sheet of frigid air” left behind when a wall of ice is broken? How about a wall of stone? Clearly a regular wall, right? What about wall of force? It’s solid, but it doesn’t block sight! What about a wall of deadly chains…? And so on.) There’s also overlap with floor/terrain properties: what’s the difference between a part of the map that’s filled with mud, and the area of effect of a transmute rock to mud spell?

(Incidentally, what is the difference—as far as our model and representation goes—between the effect created when the PC wizard casts a wall of force in combat, and a dungeon which is constructed out of walls of force? Should there be any difference?)

We have already noted that effects may be mobile (e.g., a flaming sphere spell). But effects may also be linked to another entity (which is itself potentially mobile). A common type of such effects is illumination—that is, the light shed by a glowing object or creature (and if, e.g., a character is carrying a torch, we would generally model the character as casting light, rather than having a “torch” entity which casts light and is carried by the character). “Auras” of various sorts (e.g., a frost salamander’s cold aura) are another fairly common class of example.

For now, rather than spending time on thinking deeply about how to represent things like this, we will simply note that effects & phenomena are another example of reasons to consider a wide variety of types of map elements to constitute an essentially continuous region in the space of “what sorts of things can be found on or in the map representation of a VTT”, and are yet another reason to prefer maximal flexibility in our data storage and representation format.

Elevation shifts

Not different dungeon levels—that should be represented by separate maps (or, perhaps, disjoint regions of a single map, with an enforced lack of continuity between them—more on that later in a later post). No, here we are talking about something like, for instance, a raised platform or dais, in the middle of an otherwise flat dungeon room; or a sheer cliff face, cutting across part of an outdoor map; or two platforms, with a ramp between them; etc.

It is no trouble to depict such things visually, but need they be modeled in some way relevant to BigVTT’s functionality? Once again, it’s the distance measurement functionality which suggests that the answer be “yes” (essentially the same considerations apply as do to modeling different terrain/floor types). However, actually doing this may be quite difficult, and may require carefully constructed programmatic models of the specific movement-related game mechanics used in various TTRPG systems. It may be tempting to instead model elevation changes (that do not result in “dungeon level shifts”) via something akin to transparent walls. In any case, it’s clear that some means of representing such things is desirable, else we either forego support for maps with within-level elevation shifts, or else resign ourselves to our distance measurement tools giving mistaken output when used in parts of the map where such elevation shifts occur.

Fog, visibility, illumination, etc.

A detailed discussion of fog of war and related features (vision, illumination, exploration, etc.) must wait until a later post. For now it suffices to note that there are, in general, two approaches to this sort of thing: storing and modeling fog of war metadata entirely separately from the map itself, or inferring vision/fog from features of the map.

The latter obviously requires that we model the map in a more structured and complex way than, e.g., simply a single-layer bitmap image. We have, of course, already given many reasons why we might want to do that; to those we can now add the possibility of implementing more robust fog of war / vision behavior, without requiring any (or very much) additional work on the user’s (i.e., DM’s) part. Nevertheless, we may want to keep in reserve the option of storing an entirely independent fog layer (or layers), if doing so does not mean a significant amount of additional development effort.

The reason why we might wish to do this is that effort is conserved, because information is conserved; the data which defines fog / vision must come from somewhere, and if it comes from a structured map format then someone must have encoded that structure—and if that someone is the DM himself (as seems likely, given the near-total absence of existing RPG maps in vector formats), then it’s an open question whether it takes more work to create a map which has sufficient structure from which to infer fog / vision behavior, or to use a simple, single-layer map and add an independent fog / vision metadata map on top of it.

Whichever approach we choose, we will also want to model and store the current state of the fog of war and token vision (since the dynamic nature of the fog of war feature is its whole purpose). (This is one of several kinds of map state we might want to store, along with token position and status, etc.) It is plausible that such data will be stored separately from the map as such, but this is not strictly required. Finally, as with fog / vision itself, it is possible that the state of this map layer (or layers) can be inferred or constructed from other stored data, such as the action log (see below).

Map grid

Let’s start with the disclaimer that a grid is not, strictly speaking, necessary, in order to use a VTT for its intended purpose. (And many of the VTT apps listed in my last post correctly allow the grid to be disabled.) It is true that some TTRPG systems (e.g., D&D 4e) require the use of a grid, and many others (e.g., every other edition of D&D, to one degree or another) benefit from it; so there’s no question that we must support a grid (though we must never rely on its use).

Here, however, the key question is whether we need in any sense to store any grid-related data. The answer turns out to be “yes”—namely, grid scale and grid offset. That is, consider a map like this (we are using Roll20 for this example):

Figure 1. (Click to enlarge.) 100% zoom, 1:1 scale of map image pixels to VTT map pixels.

Now, how shall we apply a map grid to this dungeon map?

Note that the grid visible in figure 1 is a part of the imported map image, not a feature of the VTT. In other words, each grid square in the map image represents a 5-foot square of the mapped region—so the battle grid that our VTT imposes on this map must match that scale.

Suppose that we use 50-pixel grid squares. Applying such a grid to this map, we get this:

Figure 2. (Click to enlarge.)

Clearly not what we want; the VTT grid squares do not match the map’s own grid scale. To solve this, we can scale down the map image until the grid on the map matches the grid of the VTT, or we can make the VTT grid squares bigger. (These operations are obviously isomorphic; which is actually preferable depends on various factors which we need not discuss at this time, except to say that ideally, BigVTT should support both options; note that many existing VTTs only support one of these—and imperfectly, at that.)

So, we go up to 70-pixel grid squares:

Figure 3. (Click to enlarge.)

Great, now the grid scales match. Unfortunately, the grid offset is wrong.

… now, what does that mean, exactly?

That is—we can see, visually, that something seems to be misaligned. But what exactly is the nature of the mismatch? After all, the grid has no reality in the game world. It’s not like the floor of this cavern is marked up with a 5-ft.-square rectilinear grid of lines! What difference does it make, actually, if we shift the grid 2.3 feet to the left? Those pixels in the map image which depict the cavern wall represent a physical wall in our fictional game world. Those pixels in the map image which form the grid represent… what? Nothing, right?

This is a perfect example of the limitations of using single-layer bitmap file formats for storing TTRPG maps. The depiction of the cavern walls and other in-game are data; the grid is metadata. But a PNG file collapses these things into a single, undifferentiated block of pixels.

In any case, we might find it convenient to specify a grid offset in some cases—such as when we must use an existing map image in bitmap format which includes a grid. Thus:

Figure 4. (Click to enlarge.)

Much better; there is no longer a distracting mismatch between two grids.

One other reason why we’d need to specify a grid offset is if we are using the “snap to grid” feature (which any self-respecting VTT must have), which constrains things like token movement, measurement, shape drawing (e.g. for manual fog reveal purposes), etc., to align with, and occur in units corresponding to, the battle grid. To see why that’s important, consider this map:

Figure 5. (Click to enlarge.)

If we use snap-to-grid for token positioning on this map, with the grid aligned as pictured, then tokens will be snapped into a position which is embedded halfway into the walls of this 5-foot-wide dungeon corridor. What we want instead is for the map to be aligned such that snap-to-grid aligns the token precisely with the corridor:

Figure 6. (Click to enlarge.)

Much better.

Note that this time, the alignment of battle grid with the grid in the map image itself is not, strictly speaking, what we are talking about. It quite unsurprisingly so happens that the grid in the map image is aligned with the dungeon hallways and rooms, but that need not be so. Indeed, the very same map from which was taken the section shown in the above two screenshots, also contains bits like this:

Figure 7. (Click to enlarge.) The hallway pictured here is half the width of a 5-ft. grid square.

And this:

Figure 8. (Click to enlarge.)

How should snap-to-grid work in such cases? Probably the answer is “it shouldn’t”. (So there must be some way to disable it temporarily, for example, or some functionality along these lines.) Still, there is no reason to create problems where none need exist, nor to avoid useful features simply because they’re not always useful; so for those maps to which snap-to-grid may unproblematically apply, we must be able to specify a grid offset.

(Actually, we can go further still. There are other transformations that we may wish to apply to a map image in order to make it fit a battle grid more precisely, such as rotation, shear / skew, or distort. For that matter, we can even apply arbitrary transformation matrices to the map image. All of the data that defines such transforms must also be stored somehow.)

Annotations

This encompasses a wide variety of map-linked metadata, of the sort that does not directly affect any of the VTT’s core functionality (e.g., positioning, token movement, fog of war, vision, etc.), but which exists to provide useful information to the DM and/or players during play. Examples might include:

• dungeon room key labels (i.e., alphanumeric tags associated with each keyed location; see The Alexandrian on dungeon keys)
• dungeon room key content (that is, the text associated with the labels—why not include it with the map, and display it on the same screen?)
• secret information (e.g., “if any character steps on that part of the floor, they will be teleported to area 27”)
  • Note that this overlaps to some extent with “disguised & hidden elements”; the key distinction, perhaps, is that by “secret information” we mean things that do not look like anything in the game world, but are only facts about other map elements
• map legend (i.e., guide to map symbols, or other hints for reading the map, displayed for easy reference)
• ephemeral region markers (e.g., “I’m going to throw a fireball right… there”)
• tags describing alterations performed by the characters (e.g., suppose that the PCs decide to start drawing crosses in chalk on the doors of dungeon rooms that they’ve explored)

In short, annotations may be textual, graphical, or some combination thereof; and they may be visible to the DM only or also to the players. In either case, they do not themselves correspond to any part of the game world (though they may describe things that do), and do not need to be modeled in any way. They do, however, need to be stored, for persistence across sessions.

Active / interactive elements

We are now getting into relatively exotic territory, but it’s worth considering (though only in passing, for now) this fairly broad category, which may include any of the following:

• animations and audio cues linked to map regions or elements
• “hyperlinks” from one map region to another (e.g., suppose that clicking on a stairway shifts the map view to a section of the map that represents whatever different dungeon level the stairway leads to)
• defined regions which restrict token movement
• map-linked triggers for action macros (these may cause map transformations to occur; tokens to appear, disappear, move, or change in some ways; etc.)

And so on; this short list barely scratches the surface of the possible. (We are getting dangerously close to re-inventing HyperCard with this sort of thing… an inevitable occupational hazard when building user-configurable dynamic multimedia systems.)

Action history

Until now, we have mostly looked at elements which define the map as it exists in some state (which may include various potential alternate states, or conditional alterations to the map state, etc., but all of these things are merely part of the totality of a single actual state). There are, in addition, many good reasons why we would also want to store a history of updates to the map state. One obvious such reason would be to implement an undo/redo feature (surely a necessity if we want BigVTT to work as a map creation/editing tool). There are several other motivations for maintaining an action / update history; we will discuss them at length in a later post.

Is all of this really necessary?

It does seem like quite a lot, doesn’t it? Is everything we’ve just listed really a mere extrapolation from the list of requirements outlined in the previous post?

I think the answer is “with a few minor exceptions, yes, it is”—but anyhow, it doesn’t matter. The point is not that we must implement all of the features and capabilities which we’ve listed in this post (much less that we must implement them right away). Rather, the reason for enumerating all of these things is to keep them in mind when making fundamental design and implementation decisions. Specifically, when choosing a data format (or formats!), we should prefer to choose such that our choice will make our lives easier when we do start implementing some of the features and functions we’ve been discussing, and avoid choosing such that our choice will make our lives harder than that regard.

What, then, are the options?

It’s crystal-clear that a simple bitmap image format won’t cut it. Indeed, it seems quite plausible that a simple bitmap image format won’t cut it even for just the map background image—never mind anything else. Any use we make of bitmap image data will have to be incorporated into a more powerful, more complex data format.

The question is: what will be that more complex data format? There are, basically, two alternatives, which can be summarized as “SVG” and “some sort of custom format”.

In fact, are these even alternatives, as such? Mightn’t we need both, after all? For instance, suppose we store the map, as such, as an SVG file (somehow), and the action log as a separate text file. Why not? Or: suppose that the map is an SVG file, but then it contains references to various bitmap images, which are each stored as separate external PNG files. No rule against that, is there?

Another way in which “alternatives” isn’t quite the right way to look at this has to do with the fact that when you’re dealing with text-based file formats, there is no sharp dividing line between almost anything and almost anything else. For instance: SVG files can contain comments. What is the difference between (a) an SVG file and a separate text file and some separate PNG files, and (b) an SVG file with some text in a comment and some base64-encoded PNG data in another comment? (Well, the latter will take up a bit more disk space, but that’s hardly fundamental!)

The nitty-gritty of just how the various parts of our data storage mechanism will fit together are, ultimately, implementation details. What’s clear, at this point, is that our approach should probably be something like “start with SVG, see how far we can push that, and branch out if need be”. It’s possible, of course, that we’ll hit a wall with that approach, and end up having to rethink the data format from scratch. But that does not seem likely enough to justify trying to design a custom data format right from the get-go.

So what does SVG get us?

Other than the advantages already listed, I mean?

Quite a lot, as it turns out.

The drawing tools just about write themselves

Recall two of our requirements: we want to have map drawing/editing tools, and we want to have fog of war support (which means the ability to reveal/conceal regions of the map). In both cases, we need to let the user draw shapes, and we need to render those shapes on the screen.

Well, the SVG format supports pretty much all the kinds of shapes that any vector drawing app could want: rectangles and ovals and polygons and lines and paths (Bezier curves)… these parts of the SVG spec effectively serve as guides for implementating the tools to draw these shapes: just create fairly straightforward mappings from user actions (clicks, pointer movements, etc.) to shape attribute values, and you’re good to go. Rendering is even more trivial: create a shape object, plug in the values, add it to the page. Easy!

Version control

SVG is a text-based format. That means that we can store our map data in a Git repository, and track changes to it, very easily.

(Is this something that anyone will want to do? On a small scale—which describes most users—probably not. But this sort of capability tends to open up options that don’t exist otherwise. For instance, collaboration on a large project, that might involve creating many BigVTT-compatible maps for some large dungeon complex, or a series of adventure paths, or a whole campaign, etc., will be greatly advantaged by the use of a version control system.)

Extensible metadata

This is a fancy term that means no more than “the format makes it easy to add support for any kind of thing”. As an XML-based file format, SVG makes it trivial to attach arbitrary amounts and kinds of information to any object, or to the file as a whole, without breaking anything, affecting any existing feature, etc.

Native support for many aspects of the design

Layers? Objects in an SVG file are naturally “layered” (the painter’s algorithm); objects can be grouped into uniquely identifiable groups; objects can be moved from layer to layer, or the layers rearranged; all of this is already a direct consequence of how the format works.

Object types? Tags and attributes. Media embedding? The <image> and <foreignObject> tags.

In short, we get many of the basics “for free”.

Composability

You can embed a bitmap image into an SVG. You can embed an SVG into another SVG. You can embed an SVG in a web page. You can embed a web page in an SVG.

As far as composability goes, if you’re working with 2D graphical data, SVG is hard to beat.

The DOM

Using SVG in a web app means having access to the Document Object Model API, which lets us manipulate all the objects that make up our map using a variety of powerful built-in functions. (“Select all character tokens”? That’s a one-liner. “Turn every wall transparent”? That’s a one-liner. “Make every goblin as big a storm giant”? Oh, you better believe that’s a one-liner.)

Compatibility

SVG is supported by every graphical browser and has been for years. There exist innumerable drawing/editing tools that can edit SVG files. SVG can be easily converted to and from a variety of other formats. (There’s now even a way to transform bitmap images into SVG files!)

What’s next?

Upcoming posts will deal with four major aspects of BigVTT’s design: affordances for working with large maps, the fog of war features, the action history feature, and the rendering system.

Having built a procedural generator which can create maps of large sections of Lacc—the shadowy City of Monoliths from the D&D adventure “Gates of Oblivion”, we now face the question of how best to use those maps.

The point of the exercise, recall, was to use these for encounter (especially combat) mapping—so that, when the player characters, while traveling through Lacc, had some sort of encounter which we wished to resolve with the aid of a local map of the PCs’ surroundings, we had ready-made maps of a large region of the city, and could select a point on that map, and locate the encounter there. Well, we’ve got the maps, but what do we do with them? How do we actually make use of them for their intended purpose?

Print them out on posters a thousand feet across? Copy chunks of them onto one of those wet-erase battle-mats (or a whole bunch of them, tiled across the floor of someone’s basement)? Something involving really big sheets of graph paper…?

… ok, yes, the obvious answer is “use a virtual tabletop”. We’ve got a digital asset (the map file in SVG format), so we just pick our favorite VTT app, upload the map, and we’re good to go. Right?

Wrong.

The problem with virtual tabletop apps

… is that they’re all bad.

That might seem like a ridiculous, intentionally inflammatory exaggeration. Well, let’s do a survey of the VTT market and see if we can find one that will support our use case.

Roll20

I’ve used this VTT website for many years (both as a DM and as a player). It’s… fine. It works well enough that I’ve continued to use it, which is about as much of an endorsement as it is reasonable to expect. So it’s the first VTT we’ll try to use for this project.

First hurdle: SVGs are not supported—only JPEGs and PNGs. Alright, we’ll just convert our SVG to PNG format; 1216×982, multiplied by 10 grid squares (50 feet) per SVG length unit, then multiplied again by 70 pixels per grid square (the standard Roll20 map scale); that gives us a PNG image 851,200×687,400 pixels in size.

Hmm. My usual image editing programs can’t actually create an image file that big! Well, maybe ImageMagick or something… but wait; before we get too far down that rabbit hole, let’s do a sanity check. This image file size calculator tells us that our PNG map would be… several hundred GB in file size. (Yes, that’s gigabytes.)

Using JPEG instead might get us down below 100 GB… but that’s small consolation, given that Roll20 only lets you upload files up to 20 megabytes in size. (For which I can hardly blame the site’s developers. Having to have your players download a hundred-gigabyte chunk of data just to view a single combat map is… not reasonable.)

Maybe we can simply convert the map on a 1-pixel-per-10-grid-square scale (i.e., the way it’s rendered in the browser, without zooming), upload that file (which will definitely be smaller than 20 MB!), and then resize it in the Roll20 map editor, stretching it out to cover our 12,160×9,820 grid squares of 70 pixels each? (After all, all the information we need is there, in those 1216×982 pixels; we guaranteed that when we made sure that all map elements would come in dimensions that were multiples of 50 feet.)

The conversion works just fine:

Figure 1. (Click to enlarge.) This is a 1216×982px PNG; file size is 41 KB.

Now we upload the file to Roll20, and add it to the map. There’s a simple UI for setting the map image’s dimensions, which is nice. (Setting its position is not so simple; we have to do a lot of laborious mouse dragging. But it’s not the worst imaginable UI flaw, and anyhow we’re about to have much bigger problems, so we’ll let this pass.)

Having set the dimensions, and aligned the map image with the grid, we zoom to 100%, and:

Figure 2. (Click to enlarge.)

Huh. What the heck is going on here? What are we even looking at?

The answer is: interpolation during image scaling.

Let’s play around with a smaller image in GraphicConverter, to how this works. Here’s a small chunk of our map:

Figure 3. A 20×20px section of the map in figure 1, taken from the top-left corner of the map.

Now we scale it up 700 times. (10x because each pixel in our PNG map represents 10 grid squares, and then 70x because each grid square is 70 pixels across, in standard Roll20 display scale.) When scaling an image, GraphicConverter offers us the option to choose from a variety of interpolation algorithms:

Figure 4. (Click to enlarge.)

Let’s try them out one at a time. Here’s “no interpolation”:

Figure 5. (Click to enlarge.) Viewing a street of Lacc, at 100% zoom level, at 70px-per-grid-square scale.

Excellent! This is exactly what we want: perfectly sharp upscaling, with every pixel of the source image rendered as a 700×700px square block of identical pixels; no blurring, no colors other than the precisely two colors that were in the source image, no shenanigans of any kind.

What if we instead use one of these other scaling algorithms? Here’s “best interpolation”:

Figure 6. (Click to enlarge.) Same view as previous figure.

Well, that’s no good… how about “normal interpolation”?

Figure 7. (Click to enlarge.) Same view as previous figure.

Nope… perhaps “smooth interpolation”?

Figure 8. (Click to enlarge.) Same view as previous figure.

Extremely nope. (Note that this looks a lot like the effect we saw in the Roll20 screenshot, in figure 2.)

The other algorithms on offer don’t change the picture that has emerged already. (“Box” and “nearest neighbor” give the same results as “no interpolation”, “sinus” is kind of like “smooth” but with the addition of weird artifacts, and the rest are variations on “smooth”.)

But this is great news, right? We’ve identified the culprit: interpolation when scaling the map image. So all we have to do is turn that off, and… uh… hm.

There isn’t actually any way to do that.

This, of course, makes Roll20 totally unusable for maps of this size.

Of course, even in the entirely counterfactual event that we could solve this problem, we’d still be faced with the fact that the Roll20 UI entirely lacks anything resembling proper affordances for working with very large maps.

For one thing, the zoom function only goes down to 10%. But 10% of 851,200px is 85,120px. Who has a display that big? I certainly don’t. Being able to view, at most, 2% of the map on the screen at any given time is, obviously, horribly unwieldy, to the point where doing anything useful with such a map is impossible. There’s also no way to quickly move the view between distant parts of the map.

I also know from experience that activating the “fog of war”, “advanced fog of war”, and “dynamic lighting” features on even a much, much smaller—but still big by the standards of the app’s apparent design intent—map (a measly couple of hundred grid squares across) leads to noticeable drops in zoom and pan performance. The lag that a user on even a fairly powerful desktop computer will experience in such cases is enough to introduce a quite frustrating degree of friction into simple map operations, and slows down the pace of combat. How much worse will that be on a map two orders of magnitude larger…?

In short: Roll20 ain’t it.

At this point, we’ll do a web search for something along the lines of “best virtual tabletop”, and click a bunch of links…

Foundry VTT

Foundry VTT appears frequently in recommendation lists for this sort of thing. Unlike Roll20, Foundry requires that the DM download and install a desktop application; the DM then uses that app to host a session from his home computer, to which players can connect via their web browsers. (There are also cloud hosting options.) Foundry is also not free; the application must be purchased, at a one-time cost of $50 (for the DM only; players need not buy anything).

As it turns out, Foundry does support maps of the size we need. It also supports SVG files. It would seem that Foundry has all the pieces in place to do exactly what we want!

Unfortunately, when we actually try to use our SVG file as the background map image, we get this:

Figure 9. (Click to enlarge.)

What the heck? Well, it seems that Foundry actually renders SVGs in an extremely dumb way: they are first rendered into bitmaps (very poorly, at a bizarrely low resolution), and then scaled (using one of the smoothing-type interpolation algorithms we saw earlier). (Why do they do it like this? Who knows, really… but a glance at the Foundry documentation entry that deals with file format support suggests that the app’s developers intended SVG files to be used primarily for character tokens and other small images; perhaps the prospect of people using SVGs for maps did not even occur to them, and so they wrote their rendering code in a way that would produce good results for tokens and such, but breaks down when applied to maps, especially very large maps. But that is only speculation on my part.)

Of course, bitmap formats, such as PNG, are also supported—but we then we again run into the same interpolation problem as with Roll20. (And, again, there is no way to disable that.)

To Foundry’s credit, it does support the full range of zoom factors, so that the full map can be seen at one time. But that’s the only concession to large-map usability; there’s no view-saving feature, nor any other UX design elements aimed at making it easy or practical to work with large maps.

Fantasy Grounds

One of the most popular and well-reviewed VTTs. I have high hopes for this one.

Sorry, no, that’s a lie. I don’t actually have high hopes for any of these apps. But I should have high hopes for Fantasy Grounds, right? Popularity of a VTT among TTRPG players is evidence that it’s very good, well-designed, feature-full, etc. (Isn’t it?) Well, let’s find out!

Fantasy Grounds is also non-free and requires installing a desktop application, like Foundry. It’s a very bloated piece of software (the installer immediately downloaded several entire game systems’ worth of support assets to my computer, without giving me any choice in the matter), with a clunky, custom-built UI that features all of the worst UI design anti-patterns of your average 1990s CRPG. Combined with the program’s extreme feature complexity, this makes it nigh-impenetrable for the starting user; as far as I can tell, the way you learn to use this thing is by watching hours upon hours of YouTube videos (the support forum is hilariously useless).

Nevertheless, I managed to figure out how to import an image and use it as a map. I still have no idea how to set grid scale, so I couldn’t say what map size (in grid squares) Fantasy Grounds supports… but it doesn’t matter, because—as with Roll20—SVG files are unsupported, and bitmap scaling makes our map worthless due to interpolation (which, as usual, cannot be disabled).

Sad! Not surprising, though. Next!

Mythic Table

A relatively new contender in the VTT arena. Web-based. Very simplistic, badly designed, and buggy (e.g. changing grid size simply does not work). More importantly for our purposes, Mythic Table doesn’t seem to have any support for maps bigger than maybe ~100 grid squares across (actually, it seems to be tied to viewport size, and a very tightly restricted zoom range). There’s no way to even attempt to use this app to do what we’re trying to do.

Role

A Roll20-esque VTT (web-based integrated video and text chat, asset management, etc.). Very new. Very sleek and “modern” look; very polished UI; very 2020s sensibilities.

Underneath the polish and sparkle? Garbage.

SVGs can be uploaded, but aren’t actually supported; the image will just be silently broken. Large map sizes can be set, but then you can’t zoom in far enough to even see the individual grid squares, much less make any kind of use them by placing tokens or what have you. (Although even zooming in as far as the app lets you do makes it clear that even if greater zoom factors were allowed, the bitmap map image would be unusable due to interpolation.)

Shmeppy

You have to pay to sign up, and there’s no demo of the GM features. As far as I can tell, there’s no SVG support. Based on a perusal of the forums and support knowledge base, I would be very surprised to learn that this VTT can do what we need here. But the documentation is very minimal and slapdash, so it’s hard to tell.

Let’s Role

What immediately struck me about this website is how heavily geared toward monetization it is. I mean, look at this account info page:

Figure 10. (Click to enlarge.)

It’s hard to tell from this page what this website even is—except for the fact that it’s all about buying content.

Well, never mind that. Does it do what we want?

Nope. No SVG support, the usual forced interpolation, and anyway it’s a moot point because the maximum map size in pixels is almost two orders of magnitude smaller than what we want. (Also the map configuration UI is bizarrely obtuse and generally poorly designed.)

Next!

Rolz

Can’t zoom out to further than 50%. Can’t specify image size in pixels or units or anything (only by dragging). Fixed total map size (128×128 grid squares).

Pathetic.

Diceweaver

Extremely obtuse UI. No SVG support. Bitmap map backgrounds (“boards”) can’t be scaled up to any kind of reasonable map size. Map size can’t even be configured.

Thoroughly bizarre app, on the whole. (I can’t imagine using it for anything, never mind just this project.)

Shard Tabletop

Very strangely designed and buggy map upload/configuration tool. Apparently does not actually let you use a map image where 1 pixel represents more than 1 grid square. You might think that SVG is a way around this (what’s a “pixel” in SVG?), but SVG map background support is even more broken than PNG map support, so… apparently not. I have no idea what the designers of this UI/feature were trying to do, but whatever it was, they don’t seem to have succeeded.

On the plus side, you can zoom in as far as you want. On the minus side, the UI as a whole is clunky.

Owlbear Rodeo

The front page of this website proclaims “ANIMATED MAPS!”. Alright. But what about regular maps? How are you at regular maps?

The answer is: I don’t know. This app seems like it’s broken in my browser—features that should be there, according to the documentation, are just absent. When I tried to log in from a different computer, to test Owlbear Rodeo on a different browser/OS setup, I got a strange error (“check server settings”, or some such).

Maybe this VTT is actually wonderful, if you can get it to work. But I couldn’t.

UPDATE: I was able to get Owlbear Rodeo to work on a different computer/browser. Unfortunately, the results were disappointing.

There’s no SVG support. PNG maps can be used, and map image size can even be set such that multiple grid squares are mapped to each grid pixel (using a fairly decent map sizing tool!). However, the usual interpolation problems ruin the map. I might be tempted to try using a statically upscaled map (despite the egregious file size required by this)… except that it is in any case impossible to zoom out to see the whole map of this size, and there are (as usual) no affordances for working with maps this large. (There is not even a zoom level indicator!)

One More Multiverse

What’s with the animated backgrounds on some of these? This sort of nonsense is absolutely terrible for performance. Well, never mind that; does OMM (as this VTT calls itself) do what we want?

Well… I can’t seem to actually create a map. At all. There does appear to be a UI for level/map creation, but… uh… it simply fails to do anything.

Oh well. Next!

D&D Beyond

Wizards of the Coast has added a VTT feature to D&D Beyond, their official digital platform. The Maps feature is currently in alpha, so perhaps it will get better, but for now, it’s useless for this sort of project: there’s no SVG support and no way to scale a bitmap map image to represent multiple grid squares per pixel (or even one grid square per pixel, for that matter).

Above VTT

An odd one, as VTTs go. Above VTT is a browser extension that integrates with D&D Beyond. I expect that it will fall out of use once WotC’s official Beyond-integrated VTT (see previous entry) is released, but for now it still works.

Above VTT seems pretty well-designed, as VTTs go. It even supports SVG maps! Unfortunately, zooming in causes performance to drop like a rock, and at a certain zoom level the browser process starts crashing outright (and even causing GPU glitches). This, obviously, makes it impossible to do anything.

Digital D20 Virtual Tabletop

Extremely slapdash effort. Spelling mistakes all over the UI, broken or incorrectly laid out components, etc. “Amateur hour” would be a compliment. In any case, SVGs are not supported, and large map sizes are not supported. Useless.

Alchemy RPG

Alchemy is the world’s first virtual tabletop (VTT) built specifically for cinematic immersion and theater of the mind style gameplay.

…

Alchemy is a Virtual Tabletop (VTT) with a slightly different focus. Whereas most others provide a map and grid as your starting point, we focus on cinematic elements, like music and environmental backgrounds, motion overlays, and more. We still have the map and grid, but we don’t think that’s the only thing players want to look at for hours during a session.

Uh… I see. What are the odds that this app has the kind of robust map features we want? Probably not great, right?

Sadly, right. No SVG support, and the most pitiful map sizing/positioning feature I have seen yet:

Figure 11. (Click to enlarge.)

It’s just a slider. And it doesn’t go past approximately 1 grid square per 135 map pixels. (What we need, of course, is 1 grid square per 0.1 map pixels.)

Oh well. At least Alchemy makes its inclinations pretty clear up-front, which is… something.

Beyond Tabletop

This one seems like a reasonably simple and straightforward VTT. I could even see myself using it… that is, if it weren’t so buggy and missing basic features like image uploading… and a bunch of other things…

In fact, it even sort of, almost, works for this project, because it does support SVGs, it does support creating a large map object (even if the grid doesn’t expand to accommodate the large map, so you can’t place tokens anywhere but a tiny part of it; and there seems to be no way to resize the battle grid, either), it renders the SVG correctly…

… but you can’t zoom out past 50%.

Quest Portal

The first VTT I’ve seen that prominently features AI. There’s some sort of “AI assistant”; there’s AI-generated art. Makes sense, really. However, not relevant to our current goal. How’s their maps feature?

Useless. No SVG support, can’t scale a map image up to fractional pixels per grid square.

Next!

Tableplop

This is the first VTT whose UI impresses me with the amount of thought that has gone into it.

Now… it’s not enough thought. There are definitely awkward parts and weird interactions. The absence of vector-drawing-app style select tools is an obvious oversight, for instance. And the absence of hotkeys for tool selection is an obvious and large oversight. Have these people never used Illustrator? Or… any other drawing app? There’s no undo/redo for drawing operations, which is just wild. The zoom feature is coded incorrectly (the zoom origin is fixed to the screen center, which violates user intuitions and makes it take much more effort to zoom in on any particular location). The menus don’t support off-axis mouse movement. Et cetera… so, I certainly wouldn’t use this app, in its current state.

But consider what it means that I’m even bothering to make criticisms like that! These guys have come pretty far indeed, for me to notice things like this, instead of just saying “lol, it’s shit”.

In any case, the UI seems designed around the combat map, which is the right approach. So maybe Tableplop can meet the challenge of our project?

Nope.

SVGs are supported, which is cool. But there’s a fixed maximum grid size (which is about two orders of magnitude too small), which is not cool. Map images can’t even be resized to cover the entire grid, which is even less cool. The resize tool is just a mouse-drag-to-resize deal, so you can’t resize precisely anyhow. (And only on the lower-right corner of an object! I was joking before about “have these guys never used a drawing app”, but now I think that… maybe they actually never have??)

In short: not even close.

Next!

D20PRO

Another desktop app. (And one that runs on my—fairly old—version of the Mac OS, at that!) Java-based. Ancient, clunky, poorly-designed UI. Nothing surprising here. What about the maps feature?

This one comes closer than most, actually! The map sizing/positioning tools are fairly advanced (if very awkward UX-wise). SVGs aren’t supported, but importing a PNG works… and you can even set the map scale all the way down to 1 grid square per 1 pixel! That’s still a factor of 10 off from what we need, but… what if we used GraphicConverter to upscale the PNG map (to 12160×9820, with no interpolation, of course), and then imported that? (It’ll be an almost 500 MB file, but that’s… maybe not too bad?)

Unfortunately, then creating the map simply fails. No error message, nothing. Just: the map-creation wizard is stuck at the last screen. Womp womp.

Eh, it’s probably a moot point, anyhow. Map zoom/pan performance was very bad, even with the 10x-scale map image; and the UI really is as clunky as they come.

Ogres Tabletop

The description / marketing materials for this VTT say all the right things, like “Instantly start preparing your game; no sign-ups or ads” and “No accounts, no ads” and “Immersive lighting system”. How’s their maps support?

Bad. SVG map images can be uploaded but are rendered incorrectly, in the same way as Foundry VTT, making them useless. Uploading a PNG map works, but it’s not possible to scale it up to fractional pixels per grid square. (Why do so many VTTs fail at this extremely basic feature? It is very easy—just look at how Roll20 does this. All you have to do is let the user specify the size, in grid squares or pixels or map units or anything, of the map image!) In any case, bitmap map images at high grid to pixel scales are ruined in the usual way, via interpolation during upscaling. Map image position can’t be set, only size. There’s a fixed maximum battle grid size. (Which, by the way, is much too small to contain the map that results when setting the map scale on our sample map to the minimum of 1 pixel per grid square.) There are no affordances for working with maps even as large as allowed…

I guess the developers’ hearts are in the right place. Alas, good intentions do not good software make.

MapTool

A very long-running VTT (plus auxiliary tools) project. Written in Java, available as desktops apps for every platform. The UI looks somewhat dated (reminiscent of Windows XP), but is actually fairly decently designed.

MapTool gets so close to getting it right. So, so close.

SVGs and PNGs are both supported. PNGs, in fact, are even scaled without interpolation. Holy s***! Someone gets it!! You can zoom in and out as far as you want. You can set the number of map image pixels (or map image units, in the case of SVGs) per grid square…

… but only as low as 9.

9!! Why 9?! Not even 10, but 9. What the hell is 9?!?

Alright. It’s fine. So we can’t use a PNG for this. (Because a 12,160×9,820-grid-square map at 9 map pixels per grid square would make for an impossibly huge file size.) But MapTool supports SVGs! So we’ll just create our SVG with all the values set at a scale of 9 (or more) map units per grid square, and…

… then the SVG map import fails.

I believe this is what they call “snatching defeat from the jaws of victory”.

Tarrasque.io

This VTT has a prominent “Tarrasque.io is going open source!” link on their front page… but the link goes to someplace called announcekit.app (an “Announcement App for Product Updates & Software Updates”)—instead of, say, a blog—and also the link is broken.

Hmm. Not a great sign. Well, how’s the VTT itself?

Well, for starters, the UI feels like it was designed by someone who knows how to design UIs. That’s already more than I can say for any of the other VTT apps reviewed in this post!

The maps feature doesn’t support SVG files. Sigh. PNG files work, but fractional map image pixels per grid square aren’t supported. Uploading a large PNG file (scaled to 1 map image pixel per grid square) technically works… but the zoom constraints prevent you from zooming in far enough to actually use the resulting map… and it’s a moot point anyway because a map file even as large as 2.2 MB (12160×9820px) drops the zoom/pan performance straight into the garbage.

Sad!

Bag of Mapping

This one’s very new. It’s also not very interesting. The UI is confusing (no, an “assistant” is not actually a substitute for having your UI make sense or work properly), and while it does support SVG maps, it does not support fractional pixels per grid square. (And client-side form field validation is also not a substitute for having your UI communicate to the user that something’s wrong!) The UX design, on the whole, is lazy and half-assed. Pass.

EpicTable

A Windows-only desktop application. No SVG support; does not support fractional pixels per grid square. (Map scaling UI is also buggy.)

If you want something done right…

Just like last time, there’s no choice but to roll my own.

Of course, building a VTT app is a much bigger project than building a tiny, single-purpose procedural generator. It’s not a matter for a single blog post; there are innumerable details to talk about (interesting and otherwise).

But the bigger the project, the more reason to start sooner instead of later, right? So, let’s get to it.

Cause for optimism

There are two major advantages that I have over all the developers of all of those VTTs I review in this post.

First, I know exactly what I need, and can make sure that my VTT has it. I’m not designing this for all D&D players, much less all TTRPG players; I’m building it for me, and people in my gaming groups. Not only does this allow me to guarantee that what I build will cover all the relevant use cases, but it also lets me make design choices that I know will perfectly suit my play style (and the play styles of my friends).

Second, I have no intention of “monetizing” this project in any way. It’ll be totally free (speech and beer). The goal here is to build something for me to use. (I would gain nothing but hassle from trying to make money off this thing, and there’s no reason not open the source.) This means that there’s no reason or incentive for me to build any features that don’t serve my purposes. I don’t need to add support for any systems except those I use; I don’t need to integrate with D&D Beyond, provide branded content, add video chat or a creator marketplace or payment processing of any kind, etc.

It’s hard to overstate the impact of these two advantages. I’m not bringing a product to market; I’m building a tool to solve a problem that I have. Nothing but time and human frailty stands between me and success.

Only two hard problems…

Working name: BigVTT.

Requirements

When it comes to requirements, details inevitably emerge in the course of development. But there are some big, obvious desiderata that we can identify in advance.

Large map support. This is the raison d’être of the entire project. BigVTT should support maps of arbitrary size (in grid squares), limited only (and limited as little as possible) by the constraints of client hardware, browser built-in maximum values, and similar inescapable limitations. There’s simply no reason to pre-emptively forbid the user from creating, say, a map of the continental United States at 5-foot-grid-square scale.¹

But simply allowing the battle grid to be set to a large size isn’t enough. We will need to ensure that BigVTT provides robust affordances for working with very large maps. This will cash out in a variety of ways, big and small; for now, it’s enough to note that we will at every step need to pay very careful attention to the entire experience (both from the DM’s side and the players’ side!) of creating, preparing, and using a very large map, in actual prep and play for an actual game. (Many unusual features and elements of UI design will emerge from this requirement, as we’ll see.)

And, of course, our app will also need to properly support the use of ordinary, small-sized maps, no less conveniently and effectively than any other VTT on the market. This should not be difficult, as it’s much easier to scale tools and UI affordances down in map size than up; still, we must not neglect to check and verify that we haven’t inadvertently somehow made the small-map use case unwieldy or problematic.

Ease of setup. It should be extremely easy to start playing. There shouldn’t be any lengthy process of first making an account, then creating a new campaign, then creating a new scene, then fumbling with a convoluted asset import UI, then… etc. Any obstacles on the path from “we should use a VTT to handle this encounter” to “ok, on my turn I move like so…” should be removed if possible, minimized otherwise.

Broad image format support. Consequence of the above two requirements. SVG maps need to be supported but not required; all other common file formats should be supported and handled properly.

Robust media management. Importing and managing images, creating maps or tokens from them, etc., should be very easy. (There should also be robust export features, though that’s a slightly more complicated matter.)

Map drawing/editing tools. It should be possible to create a map from scratch in BigVTT, using a robust set of drawing tools. Indeed, this should be easy to do, and to do quickly. It should also be possible to mark up an existing map with annotations, overlays, etc. Vector and bitmap image data should be combinable seamlessly in all of these contexts.

Tokens / effects / objects. Goes without saying, but I’m including it for completeness. Without robust token/effect/object creation/control/management, a VTT is useless.

Measurement tools. Roll20 is the gold standard here; this part of the feature roadmap just says “measurement tools at least as good as Roll20’s”.

Fog of war / illumination / vision. This feature (or, rather, cluster of related features) deserves its own post (probably multiple posts, even), but for now I will say that we don’t just want to have support for these things—we want these features to be carefully designed in such a way that using them is as painless as possible. The DM should never even be tempted to half-ass player exploration/vision state representation, much less disable it entirely, because of the overhead of using these features. (This is a remarkably common problem in many of the VTTs reviewed above.)

Compatibility. This will be a web app (because a desktop app would not be conducive to ease of setup), but the very latest bleeding-edge browser should not be required. We should make a reasonable effort to support the different browser engines as well.

Performance. It should be possible to run BigVTT on a relatively low-end laptop, a tablet, etc. It should not slow down substantially even at very large map sizes, and should not place undue stress on the user’s hardware.

Non-requirements

There’s quite a few things that many VTT apps include, that BigVTT absolutely does not need.

Voice / video chat. It would be an absolute waste of time for me to try to integrate features like this, because there’s no way I could do these things better than existing video chat services (like Discord), and anyway BigVTT does not need them, because there already are existing video chat services (like Discord).

(Text chat, however, is a possibility, mostly because it’s so easy that there’s almost no reason not to include it. But we’ll see. It’s not like there’s any shortage of available text chat options, either. Similar considerations also apply to dice-rolling.)

Providing content. Any kind of “content”, really—pre-made maps, token graphics, you name it. Totally unnecessary. I’ll just make it easy to import things. There’s no shortage out there of maps, character art, or whatever else.

Built-in game mechanics support. BigVTT is not intended to replace the DM in any way. Using the rules of the game to resolve player actions is the DM’s job. Likewise, there’s really no good reason to integrate character sheets, monster stats, etc., because that sounds like a lot of additional work for minimal benefit—such features would have to be highly system-specific, and for what? What will you do with that detailed character info? (To add insult to injury, features like this create more work not just for me as the developer of BigVTT, but for me as the DM who will use BigVTT, and for any players in games run via BigVTT! Adding things like this is worse than pointless.)

(But things like hit point / status tracking for tokens is a possibility, provided that they can be made generic enough.)

Campaign journal / wiki / forum / etc. BigVTT is a VTT. It is not a “complete integrated solution” for all your campaign-running needs. (Not that there’s anything wrong with functionality like this—far from it!—but it’s important to keep a project’s scope in check.)

(But a “show the players this image” feature—akin to Roll20’s “handouts”, but better implemented—might be useful, and in-scope.)

Fancy multimedia features. No soundtrack / visual effects / 3D dice / animated maps / etc. No fancy shit that serves no purpose except to increase the “glitz factor”.

Social media features. No “community” features, no “sharing” features, absolutely no integration with or connection to social media of any kind in any way.

Make it so

With the motivation established, and the requirements enumerated, I’m ready to begin building BigVTT.

… which is good, because I’m actually several thousand lines of code into the implementation already.

There are many fascinating details of the design and development to talk about… but that’s a matter for the next post.

In part 1, we developed a mathematical model to determine the timeline of key events in a modified version of the D&D adventure “Gates of Oblivion”, in which the player characters must repel an incursion into their home world by Lacc, the vast, shadowy City of Monoliths. This time, we’ll examine another key part of running that adventure: the maps.

The need for maps

As I noted last time, every aspect of a well-designed adventure should contribute to the adventure’s feel. In the case of “Gates of Oblivion”, the players should have a strong experience of Lacc as impossibly vast, maybe even infinite; the broad avenues (silent except for the grinding sound of great masses of stone and the distant moans of the unquiet dead) and the great monoliths of black stone should seem to stretch endlessly in all directions. From the text of the module:

The sky overhead is a featureless black, and ebon monoliths loom on all sides, divided by broad avenues. The avenues are layered with bones, many of them humanoid, though the bones of dragons and other monstrous beasts are visible as well. Some of the monoliths flicker with ghostly radiance, which does little to illuminate the darkened expanse. The blackened vault of heaven seethes with scraps of shadow, and the bone-strewn avenues are choked with tenebrous shapes that flit about without direction and purpose. In some places, vast mounds of rubble or dunes of pale sand obscure the bones of the avenue.

Lacc is a haunting and ever-shifting environment. Strings of glowing runes dance across the surfaces of the monoliths, while half-seen shapes twist and flutter across the featureless sky. Pools of sludgy black water gather inside the skulls of giant beasts, and the breeze carries the laments of countless tortured souls. Still, despite the shadows that flit through its streets, most of Lacc is desolate and empty. Though it is not truly infinite, a man would die of old age before he could cross the city on foot.

Very atmospheric!

But there’s a problem. While the module does include several combat maps (one for the interior of Xin’s tower, and one each for the immediate vicinity of the three magical Gates), they are tiny, describing, in total, less than half a square mile of area. Meanwhile, we are given a well-stocked random encounter table for Lacc, and a solid chunk of the adventure consists of traveling through the city, encountering various things, people, and creatures (many of which encounters are likely to resolve via combat).

Of course, these encounters may be resolved in the “theater of the mind” style, with the DM simply describing the environment, positioning, distances, etc.; but, for one thing, that is distinctly less fun for any players who enjoy tactical combat challenges (and if your players do not, then it’s not entirely clear why you’re running an 18th-level D&D 3.5 adventure), and for another thing, using “theater of the mind” style for encounters that take place in a strange, alien environment (as opposed to something like “a forest road”) can create a feeling of unreality and dissociation from the game world, which severely detracts from the play experience.

In many other cases similar to this one, DM might find it easy enough to quickly sketch a map of a very small section of a very large, abstractly specified environment (whether that’s a city or an extensive cavern system or whatever else), just big enough for a combat encounter… but, for one thing, that is unusually tricky in this case due to the sizes and distances involved (see below); and for another thing, being able to see the edges of the map creates a claustrophobic feeling for the players (“I want to move 100 feet that way” “Uh… that’s off the map, so…” “Eh, never mind, I’ll just… kinda… stay in this area…”), which is precisely the opposite of what we want here. (Of course the DM can improvise the off-the-map areas, but then that just makes things feel unreal again: if the DM is making the place up as he goes along, that’s pretty much the same thing as the place not really existing in any meaningful sense.)

What to do? Well, recall what we know: Lacc is vast, most of it is empty, and it’s filled with endless miles upon miles of basically the same sort of thing: bone-strewn avenues and black monoliths. Here, by the way, is what we are told about the dimensions of both of those things:

The avenues of Lacc range from 50 to 400 feet wide. Any street narrower than 100 feet wide is invariably rough terrain, as mounds of rubble and heaps of bones make progress difficult. A typical monolith is a block of black stone 200 feet wide, 200 feet long, and 600 feet tall, with a pyramidal crest (though they come in all shapes and sizes).

This is a setup that practically screams “procedural generation”.

With a simple generator, we can create, in advance, multiple (arbitrarily many, in fact) very large maps of big (i.e., a dozen miles or more across) chunks of Lacc. At any point in the adventure when the PCs are traveling through the city and encounter something interesting (i.e., something with which the encounter is worth playing out, rather than merely describing), the DM can pick a spot somewhere in the middle of one of these maps and set the encounter there. The players will then find that their characters can move even large distances in any direction, and not find themselves “off the map”—in other words, the players will feel like the characters’ surroundings really exist, can be described concretely, aren’t just being made up on the spot, etc. This sort of thing will go a very long way toward making Lacc feel like a real place. And that will, in turn, contribute to making the city feel like (ironically) a fantastic place—eerie, alien, haunting.

There’s also another major advantage of having large combat maps (i.e., that cover a large area and can support tactical-scale movement across substantial distances): it broadens the tactical scope of combat by enabling a wider variety of movement and positioning options, long-range attacks, etc. to be used in play. (Consider, for example, how rare it is to find a tactical-scale map that covers an area large enough that it is possible for two opponents to be placed on the map in such a way that they are too far apart to hit each other with a fireball. 600 feet is just 120 grid squares on a standard 5-foot-square grid, but even that evidently turns out to be too much—when did you last see a combat map that was more than 120 grid squares across?¹)

(Note that what we’re mapping here is a straightforwardly two-dimensional street layout. The hypergeometry described in the previous post is not relevant here; it’s not Lacc’s incursion into the Prime Material Plane that we’re concerned with, this time, but the landscape of the city itself, once the player characters make their way into it; and—locally, at least—Lacc will be experienced by the PCs as having the same sort of basic geometry as any other city. Of course, the DM is free to create various weird effects and consequences of Lacc’s alien nature, which may be linked to the hyperdimensionality we previously discussed—but that is beyond the scope of this post.)

Our procgen should be very simple. It should generate a layout of streets and monoliths—nothing else. (If the DM wishes to place specific things in some spots of the map, that is trivial to do, even on the fly; it’s generating the basic layout that’s the tedious and not-doable-spontaneously part, so that’s what we’re focusing on.)

Must we DIY?

Before we proceed, a seemingly reasonable question might be: why should I need to write a custom procgen for this? Surely there are innumerable D&D map generators out there already? Indeed there are, but I have been able to find none which can do, or can easily be configured to do, something that is both so simple and so specific. (This, I find, is a pattern which recurs often, whenever one determines to really do something the right way, and refuses to accept compromises for the sake of convenience.)

Let’s look at a couple of examples:

• City Generator by ProbableTrain
  • Ludicrously complex and nigh-impenetrable controls. In any case, as far as I can tell, no way to make the simple but specific sort of map I want. (Maybe I’m wrong about that, but with a UI this hard to understand, how would I know?)
• Medieval City Generator by watabou
  • Not even close. No configuration, highly opinionated city and map design.
• Fantasy Town Generator
  • Basically the same problem as the previous one.
• Random City Map Generator
  • Same problem.
• Fantasy Town Generator by donjon
  • Same problem.

None of these are even approximately what we need here. None can be configured to output a simple rectilinear grid, with arbitrary (and quite large) dimensions, consisting of streets of a certain range of widths with rectangular buildings of a certain range of sizes. It’s such a simple thing, and yet—none of these city map generators have anything even sort of like this capability. They’re just not designed to do what we want, which, again, is both extremely simple (all the graphical “frills”, all the ornamentation, all the styling details offered by all of the above generators—it is all absolutely worthless for our purposes) and very specific (any deviation whatsoever from the requirements makes the results useless, because Lacc is not a generic vaguely-medieval city with some houses and castles and such—it is the City of Monoliths, and not anything else).

There’s nothing for it: we have to write our own.

In the next section, I’ll talk about the reasoning behind the algorithm we’ll use. Afterwards, I’ll give a high-level explanation of the algorithm, and comment on some design decisions. (There’s a link to the complete code at the end of the post.)

Developing the algorithm

First, we should define some key parameters. One pair of key parameters is the permissible range of dimensions for the footprint of monoliths. (That is, we care about their width and length, not their height; of course we can also generate random height values if we wish, but since the height of a monolith does not in any way affect the heights of neighboring monoliths, no special algorithm is needed for this. We may return to this point later.)

The module text quoted above informed us that a typical monolith is “200 feet wide, 200 feet long … (though they come in all shapes and sizes)”. Let us now pick a reasonable range—say, that length and width should vary, independently and uniformly, from 150 feet to 600 feet, in 50-foot increments. (As we’ll see shortly, the 50-foot increment of variation will permit us to represent the map in a very efficient way.) We can alter the values of these parameters later, of course.

The other key parameter is the permissible set of possible street widths. This is also given in the module text: “The avenues of Lacc range from 50 to 400 feet wide.”. (We will once again assume that street widths vary in 50-foot increments.) However, for the first iteration of our algorithm, we will actually ignore this variability, and only include 50-foot-wide streets. (We will relax this restriction later, of course.)

We are ready to proceed.

Divide & conquer

One obvious approach might be the following:

1. Start with one available lot (i.e., rectangular region of map not divided by any streets running through it), spanning the whole map.
2. Grab a lot from the set of available lots.
   • If that lot is already no greater, in both dimensions, than the maximum size of a monolith (i.e., if both the lot’s length and its width are within the permissible ranges for those parameters), set it aside as claimed.
   • Otherwise, divide the lot by placing a street such that the lot is cut along its shorter axis (i.e., we want to divide a long and narrow lot into two lots of a more equitable aspect ratio, rather than dividing it into two equally long but even narrower lots).
     • Place this dividing street not necessarily equidistantly from the two ends of the lot, but at a uniformly-randomly selected position, picked in 50-foot increments from the permissible positions, which are only those positions that result in the two lots resulting from the division both being no smaller than the minimum permissible monolith size. (In other words, we do not want to end up with any lots that are too small to fit a monolith.)
     • The ends of the street should not extend beyond the boundaries of the lot.
   • For each of the two lots created by the division, if the lot is already the appropriate size (by the same criteria as above), set it aside as claimed. Otherwise, place it back into the set of available lots.
3. If there are still lots available, repeated step 2.
4. All lots should now be claimed. Place a monolith on each.
5. Done!

The code (leaving out assorted boilerplate, utility functions, etc.) is below. (Note that the distance measurements are in units of 50-foot increments, i.e. a lot width of 3 represents a lot 150 feet wide, etc. This convenient uniformity is the advantage of enforcing 50-foot increments in variation of key proportions.)

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12
};

L.lots = [ { x:      0,
			 y:      0,
			 width:  L.gridWidth,
			 height: L.gridHeight
			 } ];
L.claimedLots = [ ];

function newStreetDividingBoundingBlock(block) {
	let streetWidth = 1;
	if (block.width > block.height) {
		return {
			width:  streetWidth,
			length: block.height,
			orientation: "v",
			x: (  block.x 
				+ L.minMonolithFootprint 
				+ rollDie(block.width - 2 * L.minMonolithFootprint - streetWidth)),
			y: block.y
		};
	} else {
		return {
			width:  streetWidth,
			length: block.width,
			orientation: "h",
			x: block.x,
			y: (  block.y 
				+ L.minMonolithFootprint 
				+ rollDie(block.height - 2 * L.minMonolithFootprint - streetWidth))
		};
	}
}

function lotIsClaimable(lot) {
	return (   lot.width  <= L.maxMonolithFootprint
			&& lot.height <= L.maxMonolithFootprint);
}

function newLotsAfterStreetDividesLot(street, lot) {
	if (street.orientation == "h") {
		let topLot = {
			x:      lot.x,
			y:      lot.y,
			width:  lot.width,
			height: street.y - lot.y
		};
		let bottomLot = {
			x:      lot.x,
			y:      street.y + street.width,
			width:  lot.width,
			height: lot.y + lot.height - (street.y + street.width)
		};

		return [ topLot, bottomLot ];
	} else {
		let leftLot = {
			x:      lot.x,
			y:      lot.y,
			width:  street.x - lot.x,
			height: lot.height
		};
		let rightLot = {
			x:      street.x + street.width,
			y:      lot.y,
			width:  lot.x + lot.width - (street.x + street.width),
			height: lot.height
		};

		return [ leftLot, rightLot ];
	}
}

function subdivideLots() {
	while (L.lots.length > 0) {
		let lot = L.lots.pop();
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			newLotsAfterStreetDividesLot(newStreetDividingBoundingBlock(lot), lot).forEach(newLot => {
				if (lotIsClaimable(newLot)) {
					L.claimedLots.push(newLot);
				} else {
					L.lots.push(newLot);
				}
			});
		}
	}
}

subdivideLots();
addMonoliths(L.claimedLots);

And here’s one sample result (click to zoom in):

Figure 1. (Click to zoom in.)

Not bad! This map depicts a 60,800 foot × 49,100 foot region of Lacc. (That’s 11.5 miles × 9.3 miles, or 12,160 × 9,820 standard 5-ft. grid squares.) This is already quite large enough to create the illusion of a vast, unbounded space—and we can create as many such maps as we like.

The generator defaults to creating a map exactly as big as the browser viewport (i.e., the above map was generated by loading the demo in a browser window 1216 pixels wide by 982 pixels tall, resulting in a map 1216 units × 982 units in size; remember that 1 map unit here represents 50 feet), but that’s no intrinsic limitation; we can just as easily set the grid dimensions to something much larger—say, 10,000×10,000. That does, of course, make the code take correspondingly longer to run, and creates a correspondingly larger output file (warning: 48 MB SVG file). (A ~100-fold increase, in both cases, as both run time and output size scale linearly with area, the latter due to the fixed average monolith size and thus an expected monolith count proportional to area—the 1216×982-unit map above has ~18,000 monoliths, while the 10,000×10,000-unit map has ~1,500,000 monoliths.) A map of those dimensions represents a region of Lacc that is ~94.7 miles square, a.k.a. 100,000 standard grid squares to a side.

Not bad, as I said… but not great. The obvious flaw is that we only have one width of street represented, whereas what we’d like is a reasonable mix: a few great thoroughfares that run across great lengths of the map, some decently-wide connecting avenues between them, a bunch of medium-sized streets, and a whole lot of short little (well, “little” by the standards of the City of Monoliths) alleys.

Random street widths

We might first think to just make a minimal tweak to the above algorithm that gives each placed dividing street a random width (omitted sections of code are unchanged):

L = {
	minMonolithFootprint: 3,
	maxMonolithFootprint: 12
	streetWidths: {
		8: 0.01,
		4: 0.09,
		2: 0.25,
		1: 0.65
	}
};

function randomStreetWidth() {
	let dieSize = 100;
	let roll = rollDie(dieSize);

	let minRoll = dieSize + 1;
	for (let [ width, probability ] of Object.entries(L.streetWidths)) {
		minRoll -= probability * dieSize;
		if (roll >= minRoll)
			return parseInt(width);
	}
}

function newStreetDividingBoundingBlock(block) {
	let streetWidth;
	do {
		streetWidth = randomStreetWidth();
	} while (streetWidth > (Math.max(block.width, block.height) - L.maxMonolithFootprint));

	if (block.width > block.height) {
		return {
			width:  streetWidth,
			length: block.height,
			orientation: "v",
			x: (  block.x 
				+ L.minMonolithFootprint 
				+ rollDie(block.width - 2 * L.minMonolithFootprint - streetWidth)),
			y: block.y
		};
	} else {
		return {
			width:  streetWidth,
			length: block.width,
			orientation: "h",
			x: block.x,
			y: (  block.y 
				+ L.minMonolithFootprint 
				+ rollDie(block.height - 2 * L.minMonolithFootprint - streetWidth))
		};
	}
}

Notice that we’ve specified the distribution of street widths that our algorithm should sample from when attempting to place a street: 400-ft.-wide (a.k.a width of 8 units) streets—1%; 200-ft.-wide—9%; 100-ft.-wide—25%; 50-ft.-wide—65%. (The resulting distribution of street widths in the generated map will be somewhat different from this—more skewed toward narrower streets, to be precise—because the widths of dividable lots at each iteration will increasingly limit the average maximum width of a street that can fit in a lot).

Unfortunately, the result is not what we want:

Figure 2. (Click to zoom in.)

This looks wrong. The problem here is that wider streets should, in general, be longer than narrow streets; having broad avenues that go for only a tiny distance is weird—you never see this sort of thing in a real city. To be precise, what we want is for a street to be able to cut across any orthogonal-orientation street that is narrower than it. So the broadest avenues could span the whole map, while most of the small alleys would run only between the two nearest larger streets.

(Actually, is that quite right? Hold that thought; we’ll come back to it. For now, let’s take for granted the desideratum described in the previous paragraph.)

Drawing lots

Let’s try a different approach. Instead of iterating over lots and subdividing them, we will do the following:

1. Randomly select a street width and an orientation.
2. Selecting from only those lots in which a street of the selected width and orientation can fit (without resulting, after dividing the lot, in the creation of any lot that’s too small to contain a monolith), pick a random such lot.
   • If no lot can be found that fits a street of the selected width and orientation, go back to step 1.
3. Place the street in the selected lot (at a random position within the lot, selecting from only those positions that satisfy the constraint described in the previous step). (This will divide the lot into two lots.)
   • For each of the two newly created lots, check whether the lot is ready to have a monolith placed on it. If so, set it aside as claimed. Otherwise, place it back into the set of available lots.
4. If any available lots remain, repeat from step 1.

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12,

	streetWidths: {
		8: 0.02,
		4: 0.08,
		2: 0.25,
		1: 0.65
	}
};

function newLotsAfterStreetDividesLot(street, lot) {
	if (street.orientation == "h") {
		let topLot = {
			x:      lot.x,
			y:      lot.y,
			width:  lot.width,
			height: street.y - lot.y,
			left:   lot.left,
			right:  lot.right,
			top:    lot.top,
			bottom: street.y
		};
		let bottomLot = {
			x:      lot.x,
			y:      street.y + street.width,
			width:  lot.width,
			height: lot.bottom - (street.y + street.width),
			left:   lot.left,
			right:  lot.right,
			top:    street.y + street.width,
			bottom: lot.bottom
		};

		return [ topLot, bottomLot ];
	} else {
		let leftLot = {
			x:      lot.x,
			y:      lot.y,
			width:  street.x - lot.x,
			height: lot.height,
			left:   lot.left,
			right:  street.x,
			top:    lot.top,
			bottom: lot.bottom
		};
		let rightLot = {
			x:      street.x + street.width,
			y:      lot.y,
			width:  lot.right - (street.x + street.width),
			height: lot.height,
			left:   street.x + street.width,
			right:  lot.right,
			top:    lot.top,
			bottom: lot.bottom
		};

		return [ leftLot, rightLot ];
	}
}

function lotIsClaimable(lot) {
	return (   lot.width  <= L.maxMonolithFootprint
			&& lot.height <= L.maxMonolithFootprint);
}

function getRandomStreetWidth() {
	let dieSize = 100;
	let roll = rollDie(dieSize);

	let minRoll = dieSize + 1;
	for (let [ width, probability ] of Object.entries(L.streetWidths)) {
		minRoll -= probability * dieSize;
		if (roll >= minRoll)
			return parseInt(width);
	}
}

function getRandomOrientation() {
	return (rollDie(2) - 1) ? "h" : "v";
}

function getRandomLot(width, orientation) {
	let suitableLots = L.lots.filter(lot => {
		if (orientation == "h") {
			return lot.height >= 2 * L.minMonolithFootprint + width;
		} else {
			return lot.width >= 2 * L.minMonolithFootprint + width;
		}
	});

	let orientationString = orientation == "h" ? "horizontal" : "vertical";

	if (suitableLots.length == 0)
		return null;
	else
		return suitableLots[rollDie(suitableLots.length) - 1];
}

function getRandomPointInLot(lot, width, orientation) {
	if (lot == null)
		return null;

	if (orientation == "h") {
		return {
			x: lot.x + Math.floor(lot.width / 2),
			y: lot.y + L.minMonolithFootprint + rollDie(lot.height - 2 * L.minMonolithFootprint - width)
		};
	} else {
		return {
			x: lot.x + L.minMonolithFootprint + rollDie(lot.width - 2 * L.minMonolithFootprint - width),
			y: lot.y + Math.floor(lot.height / 2)
		};
	}
}

function placeRandomStreet() {
	if (L.lots.length == 0)
		return false;

	let width = getRandomStreetWidth();

	let orientation = getRandomOrientation();

	let lot = getRandomLot(width, orientation);
	let position = getRandomPointInLot(lot, width, orientation);

	if (position == null)
		return true;

	let length = orientation == "h" 
				 ? lot.width 
				 : lot.height;
	if (orientation == "h") {
		position.x = lot.x;
	} else {
		position.y = lot.y;
	}

	L.lots.remove(lot);
	newLotsAfterStreetDividesLot({
		width:  width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	}, lot).forEach(newLot => {
		if (lotIsClaimable(newLot)) {
			L.claimedLots.push(newLot);
		} else {
			L.lots.push(newLot);
		}
	});

	return true;
}

while(placeRandomStreet());

addMonoliths(L.claimedLots);

Figure 3. (Click to zoom in.)

We’re making progress! We’ve still got a lot of those short, wide streets, though…

Unbounded extension

Perhaps we can simply extend each street we place past the bounds of the lot we’re placing it in, all the way to the edges of the map? Of course, when placing a street, we will have to divide not only the lot we picked out, but all the other lots which that street will intersect. Like so (as before, unchanged code is omitted):

function placeRandomStreet() {
	if (L.lots.length == 0)
		return false;

	let width = getRandomStreetWidth();

	let orientation = getRandomOrientation();

	let lot = getRandomLot(width, orientation);
	let position = getRandomPointInLot(lot, width, orientation);

	if (position == null)
		return true;

	let length = orientation == "h" 
				 ? L.gridWidth 
				 : L.gridHeight;
	if (orientation == "h") {
		position.x = 0;
	} else {
		position.y = 0;
	}

	let newStreet = {
		width:  width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	};
	let lotsAfterSubdividing = [ ];
	for (let lot of L.lots) {
		if (streetIntersectsLot(newStreet, lot)) {
			lotsAfterSubdividing.push(...(newLotsAfterStreetDividesLot(newStreet, lot)));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}
	for (let lot of L.claimedLots) {
		if (streetIntersectsLot(newStreet, lot)) {
			lotsAfterSubdividing.push(...(newLotsAfterStreetDividesLot(newStreet, lot)));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}	
	L.lots = [ ];
	L.claimedLots = [ ];
	for (let lot of lotsAfterSubdividing) {
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.lots.push(lot);
		}
	}

	return true;
}

while(placeRandomStreet());

addMonoliths([ ...L.lots, ...L.claimedLots ]);

Figure 4. (Click to zoom in.)

Hmm. Not quite.

Top-down planning

Let’s revisit the question of which streets should be able to cut across which other streets. We said before that wider streets should be able to cut across narrower streets, but not vice-versa; but what does that actually mean? If street A intersects street B, then street B by definition also intersects street A. Yet there’s clearly something wrong with both figure 4 and figure 2 (and, to a slightly lesser extent, figure 3), which has to do with what streets intersect what others.

Recall what we said we want to see: “a few great thoroughfares that run across great lengths of the map, some decently-wide connecting avenues between them, a bunch of medium-sized streets, and a whole lot of short little alleys”. So, the widest streets should run all the way across the map, but a small alley should not run all the way across the map. One way to think about this is to imagine the city layout being planned in stages: first we place the widest streets, then we place slightly narrower streets in the lots between those widest streets (but never crossing the boundaries of those lots), then we place even narrower streets in the lots that remain, etc., until we’ve reached the narrowest street type, which we can continue placing until we’ve subdivided all the lots down to our desired size.

The problem with implementing this approach algorithmically is that having started placing streets of width 8, say, we don’t know when to stop—how many such streets should we have? When can we say “that’s enough streets of width 8, let’s now start placing streets of width 4”? Since we’re placing streets in order of width, we can’t rely on random sampling from a defined probability distribution to give us (an approximation to) the street width frequency distribution we’re going for.

However, perhaps we can cheat, by means of a simple heuristic. The code that produced figure 3 results in ~23,000 streets at a grid size of 1216×982 (that’s in width units representing 50 feet each, remember, not feet or grid squares). Let’s round that down to 20,000, and then simply create as many streets of each type as we estimate there should be, given our desired street width frequency distribution. (That distribution will not match the probability distributions we’ve been using in the previous code samples, because there, the width of a placed street was constrained by the average available lot size. Since that won’t meaningfully be the case any longer, we’ll have to adjust the frequencies significantly downwards for the larger street widths, e.g. there certainly cannot be 200 or 400 streets of width 8 on a 1216×982 map!)

A bit of tweaking of the frequencies, and we have (omitted code unchanged, as before):

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12,

	streetWidths: {
		8: 0.00002,
		4: 0.00028,
		2: 0.00470,
		1: 0.99500
	}
};

function placeRandomStreet(streetWidth) {
	if (L.lots.length == 0)
		return false;

	let width = streetWidth;

	let orientation = getRandomOrientation();

	let lot = getRandomLot(width, orientation);
	let position = getRandomPointInLot(lot, width, orientation);

	if (position == null)
		return true;

	let length = orientation == "h" 
				 ? lot.width 
				 : lot.height;
	if (orientation == "h") {
		position.x = lot.x;
	} else {
		position.y = lot.y;
	}

	let newStreet = {
		width:  width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	});

	let lotsAfterSubdividing = [ ];
	for (let lot of L.lots) {
		if (streetIntersectsLot(newStreet, lot)) {
			lotsAfterSubdividing.push(...(newLotsAfterStreetDividesLot(newStreet, lot)));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}
	L.lots = [ ];
	for (let lot of lotsAfterSubdividing) {
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.lots.push(lot);
		}
	}

	return true;
}

let totalNumStreets = 2E4;
let streetWidthsInReverseOrder = [ ...(Object.keys(L.streetWidths).sort()) ].reverse();
for (let width of streetWidthsInReverseOrder) {
	width = parseInt(width);
	let numStreetsOfThisWidth = L.streetWidths[width] * totalNumStreets;
	for (let i = 0; i < numStreetsOfThisWidth; i++)
		placeRandomStreet(width);
}

addMonoliths([ ...L.lots, ...L.claimedLots ]);

Figure 5. (Click to zoom in.)

We’re making progress!

We’ve got a bunch of un-subdivided lots in there, though (the large blocks of black). Those definitely exceed our defined monolith size ranges. Now, we could adjust our anticipated total street count upwards, and tweak the defined street width frequency distribution… but that seems like a very fragile solution (even more so than the heuristic we’re already using).

A mixed approach

For a more robust fix, let’s bring back the approach we started with (which generated the map shown in figure 5): subdividing lots until all lots are suitably small. We will do this after we have placed all the streets as per the previous code sample:

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12,

	streetWidths: {
		8: 0.00002,
		4: 0.00028,
		2: 0.00470,
		1: 0.99500
	}
};

function placeRandomStreet(streetWidth) {
	if (L.lots.length == 0)
		return false;

	let width = streetWidth;

	let orientation = getRandomOrientation();

	let lot = getRandomLot(width, orientation);
	let position = getRandomPointInLot(lot, width, orientation);

	if (position == null)
		return true;

	let length = orientation == "h" 
				 ? lot.width 
				 : lot.height;
	if (orientation == "h") {
		position.x = lot.x;
	} else {
		position.y = lot.y;
	}

	let newStreet = {
		width:  width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	});

	let lotsAfterSubdividing = [ ];
	for (let lot of L.lots) {
		if (streetIntersectsLot(newStreet, lot)) {
			lotsAfterSubdividing.push(...(newLotsAfterStreetDividesLot(newStreet, lot)));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}
	L.lots = [ ];
	for (let lot of lotsAfterSubdividing) {
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.lots.push(lot);
		}
	}

	return true;
}

function newStreetDividingBoundingBlock(block) {
	let streetWidth = 1;
	if (block.width > block.height) {
		return {
			width:  streetWidth,
			length: block.height,
			orientation: "v",
			x: (  block.x 
				+ L.minMonolithFootprint 
				+ rollDie(block.width - 2 * L.minMonolithFootprint - streetWidth)),
			y: block.y
		};
	} else {
		return {
			width:  streetWidth,
			length: block.width,
			orientation: "h",
			x: block.x,
			y: (  block.y 
				+ L.minMonolithFootprint 
				+ rollDie(block.height - 2 * L.minMonolithFootprint - streetWidth))
		};
	}
}

function subdivideLots() {
	while (L.lots.length > 0) {
		let lot = L.lots.pop();
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.streets.push(newStreetDividingBoundingBlock(lot));
			newLotsAfterStreetDividesLot(L.streets.last, lot).forEach(newLot => {
				if (lotIsClaimable(newLot)) {
					L.claimedLots.push(newLot);
				} else {
					L.lots.push(newLot);
				}
			});
		}
	}
}

let totalNumStreets = 2E4;
let streetWidthsInReverseOrder = [ ...(Object.keys(L.streetWidths).sort()) ].reverse();
for (let width of streetWidthsInReverseOrder) {
	width = parseInt(width);
	let numStreetsOfThisWidth = L.streetWidths[width] * totalNumStreets;
	for (let i = 0; i < numStreetsOfThisWidth; i++)
		placeRandomStreet(width);
}

subdivideLots();

addMonoliths([ ...L.lots, ...L.claimedLots ]);

Figure 6. (Click to zoom in.)

Definitely starting to get somewhere.

One problematic behavior that this algorithm has is that it often places parallel wide streets much closer to one another than is plausible. You can see many cases of this in the preceding two samples, e.g.:

Figure 7. (Click to zoom in.)

Breathing room

So let’s explicitly correct for this. We’ll introduce a “repulsion factor”, which will prevent streets from being too close to each other. Streets will repel one another in proportion to width—specifically, the width of the narrower of two streets. Thus, a narrow street can be close to a narrow street, or to a wide street; but two wide streets must be further apart. Each time we pick a random location to place a street, we’ll check whether it’s too close to another street, according to this repulsion factor; if so, we’ll try again with another random location.

And so (unchanged code omitted, as before):

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12,

	streetWidths: {
		8: 0.00010,
		4: 0.00090,
		2: 0.00900,
		1: 0.99000
	},

	streetRepulsionFactor: 10
};

function streetsBoundingLot(lot) {
	let boundingStreets = L.streets.filter(street => {
		if (street.orientation == "h") {
			return (   (   street.y + street.width == lot.top
						|| lot.bottom == street.y)
					&& (   street.x < lot.right
						&& street.x + street.length > lot.left));

		} else {
			return (   (   street.x + street.width == lot.left
						|| lot.right == street.x)
					&& (   street.y < lot.bottom
						&& street.y + street.length > lot.top));
		}
	});

	let streets = {
		all: boundingStreets
	};
	for (let boundingStreet of boundingStreets) {
		if (boundingStreet.y + boundingStreet.width == lot.top)
			streets.top = boundingStreet;
		if (lot.bottom == boundingStreet.y)
			streets.bottom = boundingStreet;
		if (boundingStreet.x + boundingStreet.width == lot.left)
			streets.left = boundingStreet;
		if (lot.right == boundingStreet.x)
			streets.right = boundingStreet;
	}

	return streets;
}

function placeRandomStreet(streetWidth) {
	if (L.lots.length == 0)
		return false;

	let width = streetWidth;

	let orientation = getRandomOrientation();

	let lot = getRandomLot(width, orientation);
	let position = getRandomPointInLot(lot, width, orientation);

	if (position == null)
		return false;

	let boundingStreets = streetsBoundingLot(lot);
	if (orientation == "h") {
		let spaceAbove = position.y - (boundingStreets.top.y + boundingStreets.top.width);
		let spaceBelow = boundingStreets.bottom.y - (position.y + width);

		let minSpaceAbove = Math.max(L.minMonolithFootprint, 
									 Math.min(width, boundingStreets.top.width || width)    * L.streetRepulsionFactor);
		let minSpaceBelow = Math.max(L.minMonolithFootprint,
									 Math.min(width, boundingStreets.bottom.width || width) * L.streetRepulsionFactor);

		if (   spaceAbove < minSpaceAbove
			|| spaceBelow < minSpaceBelow)
			return false;
	} else {
		let spaceLeft = position.x - (boundingStreets.left.x + boundingStreets.left.width);
		let spaceRight = boundingStreets.right.x - (position.x + width);

		let minSpaceLeft = Math.max(L.minMonolithFootprint, 
									Math.min(width, boundingStreets.left.width || width)   * L.streetRepulsionFactor);
		let minSpaceRight = Math.max(L.minMonolithFootprint,
									 Math.min(width, boundingStreets.right.width || width) * L.streetRepulsionFactor);

		if (   spaceLeft  < minSpaceLeft
			|| spaceRight < minSpaceRight)
			return false;
	}

	let length = orientation == "h" 
				 ? lot.width 
				 : lot.height;
	if (orientation == "h") {
		position.x = lot.x;
	} else {
		position.y = lot.y;
	}

	L.streets.push({
		width:  width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	});

	let lotsAfterSubdividing = [ ];
	for (let lot of L.lots) {
		if (streetIntersectsLot(L.streets.last, lot)) {
			lotsAfterSubdividing.push(...(newLotsAfterStreetDividesLot(L.streets.last, lot)));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}
	L.lots = [ ];
	for (let lot of lotsAfterSubdividing) {
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.lots.push(lot);
		}
	}

	return true;
}

let totalNumStreets = 2E4;
let streetWidthsInReverseOrder = [ ...(Object.keys(L.streetWidths).sort()) ].reverse();
for (let width of streetWidthsInReverseOrder) {
	width = parseInt(width);
	let desiredNumStreetsOfThisWidth = L.streetWidths[width] * totalNumStreets;
	let numStreetsOfThisWidth = 0;
	if (width > 1) {
		while (numStreetsOfThisWidth < desiredNumStreetsOfThisWidth) {
			if (placeRandomStreet(width))
				numStreetsOfThisWidth++;
		}
	} else {
		for (let i = 0; i < desiredNumStreetsOfThisWidth; i++)
			placeRandomStreet(width);
	}
}

subdivideLots();

addMonoliths(L.claimedLots);

Figure 8. (Click to zoom in.)

Not too bad.

We’ve definitely reached the point where we can generate maps (in as great a quantity as we please) which have the property that they locally look plausible at pretty much any point, and offer a variety of types of street configurations (from great highways with smaller avenues branching off them, to haphazardly-arranged warrens of alleys). In other words, this is already usable for the purpose of picking an arbitrary location somewhere in the middle of the map and setting an encounter there (which is what we wanted in the first place).

Still, there are some problems. One obvious problem is that the algorithm is fragile and contains multiple “magic numbers” which must be tweaked in an ad-hoc manner to produce desired results—an expected street count (which doesn’t even end up matching the street count in the resulting map; the map shown in figure 8, for example, has ~15,000 streets, not ~20,000), and a carefully tweaked expected street width frequency distribution (which also doesn’t end up matching the actual frequency distribution of streets in the resulting map). The former, in particular, has to be adjusted for different map sizes (though perhaps we could pick a reasonably suitable number automatically as some function of map size…). Robust and flexible, it ain’t.

Even setting aside implementation details, though, something about this map (and this is true of basically all maps created by this version of the algorithm) looks wrong—unnatural, somehow. This is not necessarily a problem for our very specific motivating purpose (using one or more such maps as settings for random encounters while traveling through the City of Monoliths)… but, as with our other design decisions so far, it would be better if every aspect of the design contributed to the feel of the adventure, while avoiding any visibly artificial-seeming elements.

Clumping

Why does the map shown in figure 8 look vaguely wrong? On close inspection, we can see that it has two odd properties. First, this algorithm has a tendency to subdivide some parts of the map many times (producing regions with many streets of intermediate width and heterogeneous sizes of “blocks” between them), while leaving other parts of the map relatively uniform (producing large regions with only small alleys, and no intermediate-width streets crossing them).

This is easier to see if we pause the generator in the middle of the process, before any streets of width 1 have been placed. Here’s one map with only streets of width 2 or greater:

Figure 9. (Click to zoom in.)

And here’s a map with only streets of width 4 or greater:

Figure 10. (Click to zoom in.)

Whether this effect is good or bad by itself is probably a question of aesthetics (although in combination with the next quirk, it’s definitely bad). But why does it happen? Actually, that’s a pretty straightforward mathematical consequence of how the street-placement algorithm works. Remember that when placing a street, we select a random point at which to (attempt to) place the street by first picking an un-subdivided lot at random, with the distribution across lots being uniform and—importantly—not weighted by lot size. Now suppose that we place two streets, like this:

Figure 11. (Click to zoom in.)

We now have three lots—and each of them has an equal chance to be selected for attempted street placement! The top two lots together cover a smaller area than the bottom lot, and the top-left lot covers a smaller area than the top-right lot—which means that, when selecting a random lot to place a street in, that street is more likely to be placed closer to the top edge of the map than to the bottom edge, and more likely to be placed closer to the left edge of the map than to the right edge. And the more streets we place in some region of the map, the more lots we create there, and the more likely it becomes that further streets will be placed in that region, etc. Of course, the relatively likelihood that a street will be place in some part of the map levels off once the repulsion effect and the minimum lot size rule start to prevent streets from being placed in more and more of the randomly chosen points in that part of the map… but by then, most or all of the widest and intermediate-width streets have been placed, and the skew in the distribution of street widths by map region is already in place.

Whither crossroads?

The other odd property of maps generated by this algorithm can be seen if we take a close look at the map in figure 8. Take a look at the intersections between streets. Notice anything odd?

There are almost no X-intersections (a.k.a. crossroads).

There’s plenty of T-intersections, of course. But very few where two streets cross and both of them continue in both directions—and only one such intersection involving streets of width greater than 1!

This is, actually, pretty weird. Real cities tend to have plenty of X-intersections; their near-total absence from this map is a large part of what makes it look vaguely artificial. The way this algorithm is written means that narrower streets can never cut across wider streets… but that turns out to mean that the reverse is also true, with the result that streets don’t cut across one another at all. (The few existing X-intersections are created by coincidence—each consists not of two streets, but of three, with two coincidentally-collinear streets meeting, at the same point, a third which is orthogonal to the other two.)

Another way to look at the city layout that results from this is that there is no way out of a region of the map except by traversing increasingly wide avenues. In effect, there are no “take the local streets” routes as alternatives to the major thoroughfares. This has the effect of making the map less interesting on a large scale. (Again, this is not relevant for the very specific purpose of using the map to run disjoint encounters, each of which is localized to a small sub-region; however, it would be preferable if these maps we are generating could stand up to a bit more prodding and “off-label use” without their Potemkin facades collapsing.)

Robert Moses would approve

Let’s take a third crack at the idea that wide streets should be able to cut across narrower streets, but not vice-versa. Consider what happens if we once again place streets not in descending width order, but randomly (as in figure 3), allowing a street to extend past the ends of the lot we placed it in (unlike in figure 3), but not necessarily all the way to the edges of the map (unlike in figure 4). Instead, we will extend each street, in either direction, only until it hits another street of the same width or wider (or the edge of the map).²

The full code (sans boilerplate / utility functions):

L = {
	gridWidth: window.innerWidth,
	gridHeight: window.innerHeight,

	minMonolithFootprint: 3,
	maxMonolithFootprint: 12,

	streetWidths: {
		8: 0.02,
		4: 0.08,
		2: 0.25,
		1: 0.65
	},

	streetRepulsionFactor: 10,
};

L.lots = [ { x:      0,
			 y:      0,
			 width:  L.gridWidth,
			 height: L.gridHeight,
			 left:   0,
			 right:  L.gridWidth,
			 top:    0,
			 bottom: L.gridHeight
			 } ];
L.claimedLots = [ ];
L.streets = [
	{ width: 0,
	  length: L.gridWidth,
	  orientation: "h",
	  x: 0,
	  y: 0
	  },
	{ width: 0,
	  length: L.gridHeight,
	  orientation: "v",
	  x: 0,
	  y: 0
	  },
	{ width: 0,
	  length: L.gridWidth,
	  orientation: "h",
	  x: 0,
	  y: L.gridHeight
	  },
	{ width: 0,
	  length: L.gridHeight,
	  orientation: "v",
	  x: L.gridWidth,
	  y: 0
	  }
];

function newLotsAfterStreetDividesLot(street, lot) {
	let newLots = [ ];

	if (street.orientation == "h") {
		let topLot = {
			x:      lot.x,
			y:      lot.y,
			width:  lot.width,
			height: street.y - lot.y,
			left:   lot.left,
			right:  lot.right,
			top:    lot.top,
			bottom: street.y
		};
		let bottomLot = {
			x:      lot.x,
			y:      street.y + street.width,
			width:  lot.width,
			height: lot.bottom - (street.y + street.width),
			left:   lot.left,
			right:  lot.right,
			top:    street.y + street.width,
			bottom: lot.bottom
		};

		if (topLot.width    * topLot.height    > 0)
			newLots.push(topLot);

		if (bottomLot.width * bottomLot.height > 0)
			newLots.push(bottomLot);
	} else {
		let leftLot = {
			x:      lot.x,
			y:      lot.y,
			width:  street.x - lot.x,
			height: lot.height,
			left:   lot.left,
			right:  street.x,
			top:    lot.top,
			bottom: lot.bottom
		};
		let rightLot = {
			x:      street.x + street.width,
			y:      lot.y,
			width:  lot.right - (street.x + street.width),
			height: lot.height,
			left:   street.x + street.width,
			right:  lot.right,
			top:    lot.top,
			bottom: lot.bottom
		};

		if (leftLot.width  * leftLot.height  > 0)
			newLots.push(leftLot);

		if (rightLot.width * rightLot.height > 0)
			newLots.push(rightLot);
	}

	return newLots;
}

function lotIsClaimable(lot) {
	return (   lot.width  <= L.maxMonolithFootprint
			&& lot.height <= L.maxMonolithFootprint);
}

function getRandomStreetWidth() {
	let dieSize = 100;
	let roll = rollDie(dieSize);

	let minRoll = dieSize + 1;
	for (let [ width, probability ] of Object.entries(L.streetWidths)) {
		minRoll -= probability * dieSize;
		if (roll >= minRoll)
			return parseInt(width);
	}
}

function getRandomOrientation() {
	return (rollDie(2) - 1) ? "h" : "v";
}

function getRandomLot(width, orientation) {
	let suitableLots = L.lots.filter(lot => {
		if (orientation == "h") {
			return lot.height >= 2 * L.minMonolithFootprint + width;
		} else {
			return lot.width >= 2 * L.minMonolithFootprint + width;
		}
	});

	let orientationString = orientation == "h" ? "horizontal" : "vertical";

	if (suitableLots.length == 0)
		return null;
	else
		return suitableLots[rollDie(suitableLots.length) - 1];
}

function getRandomPointInLot(lot, width, orientation) {
	if (lot == null)
		return null;

	if (orientation == "h") {
		return {
			x: lot.x + Math.floor(lot.width / 2),
			y: lot.y + L.minMonolithFootprint + rollDie(lot.height - 2 * L.minMonolithFootprint - width)
		};
	} else {
		return {
			x: lot.x + L.minMonolithFootprint + rollDie(lot.width - 2 * L.minMonolithFootprint - width),
			y: lot.y + Math.floor(lot.height / 2)
		};
	}
}

function getRandomPoint(width, orientation) {
	return getRandomPointInLot(getRandomLot(width, orientation), width, orientation);
}

function getBoundingBlockAtPoint(point, options) {
	options = Object.assign({
		streetWidth: 1,
		orientation: null
	}, options);

	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >= options.streetWidth 
		   	)
		&& street.orientation != options.orientation
	);

	let compareFunction = (a, b) => {
		if (a.orientation == "v") {
			if (a.x < b.x)
				return -1;
			if (a.x > b.x)
				return 1;
			return 0;
		} else {
			if (a.y < b.y)
				return -1;
			if (a.y > b.y)
				return 1;
			return 0;
		}
	};

	let nearestStreetLeft, nearestStreetRight, nearestStreetAbove, nearestStreetBelow;
	let blockLeft, blockTop, blockRight, blockBottom;

	let lotAtPoint = L.lots.find(lot => 
		   lot.left   <= point.x
		&& lot.right  >= point.x
		&& lot.top    <= point.y
		&& lot.bottom >= point.y
	);
	if (lotAtPoint == null)
		return null;

	if (options.orientation == "h") {
		nearestStreetLeft = crossStreets.filter(street => 
			   street.x <= point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).last;
		nearestStreetRight = crossStreets.filter(street => 
			   street.x > point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).first;

		blockLeft = nearestStreetLeft.x + nearestStreetLeft.width;
		blockRight = nearestStreetRight.x;

		blockTop = lotAtPoint.top;
		blockBottom = lotAtPoint.bottom;
	} else {
		nearestStreetAbove = crossStreets.filter(street =>
			   street.y <= point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).last;
		nearestStreetBelow = crossStreets.filter(street => 
			   street.y > point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).first;

		blockTop = nearestStreetAbove.y + nearestStreetAbove.width;
		blockBottom = nearestStreetBelow.y;

		blockLeft = lotAtPoint.left;
		blockRight = lotAtPoint.right;
	}

	return {
		x:      blockLeft,
		y:      blockTop,
		width:  blockRight - blockLeft,
		height: blockBottom - blockTop,
		left:   blockLeft,
		right:  blockRight,
		top:    blockTop,
		bottom: blockBottom
	}
}

function streetIntersectsLot(street, lot) {
	if (street.orientation == "h") {
		if (   street.x < lot.right
			&& street.x + street.length > lot.x
			&& street.y < lot.bottom
			&& street.y + street.width > lot.y)
			return true;
	} else {
		if (   street.y < lot.bottom
			&& street.y + street.length > lot.y
			&& street.x < lot.right
			&& street.x + street.width > lot.x)
			return true;
	}

	return false;
}

function placeRandomStreet() {
	if (L.lots.filter(lot => lot.width * lot.height > 0).length == 0)
		return false;

	let width = getRandomStreetWidth();

	let orientation = getRandomOrientation();

	let position = getRandomPoint(width, orientation);
	if (position == null)
		return true;

	let boundingBlock = getBoundingBlockAtPoint(position, {
		streetWidth: width,
		orientation: orientation
	});

	if (boundingBlock == null)
		return true;

	let length = orientation == "h" 
				 ? boundingBlock.width 
				 : boundingBlock.height;

	if (orientation == "h") {
		position.x = boundingBlock.x;
	} else {
		position.y = boundingBlock.y;
	}

	L.streets.push({
		width: width,
		length: length,
		orientation: orientation,
		x: position.x,
		y: position.y
	});

	let lotsAfterSubdividing = [ ];
	for (let lot of [ ...L.lots, ...L.claimedLots ]) {
		if (streetIntersectsLot(L.streets.last, lot)) {
			lotsAfterSubdividing.push(...newLotsAfterStreetDividesLot(L.streets.last, lot));
		} else {
			lotsAfterSubdividing.push(lot);
		}
	}
	L.lots = [ ];
	L.claimedLots = [ ];
	for (let lot of lotsAfterSubdividing) {
		if (lotIsClaimable(lot)) {
			L.claimedLots.push(lot);
		} else {
			L.lots.push(lot);
		}
	}

	return true;
}

while(placeRandomStreet());

addMonoliths(L.claimedLots);

And the result:

Figure 12. (Click to zoom in.)

Hmm. Something has gone wrong here. On closer inspection, we can see that most of what at first look like very wide streets, are actually just narrower streets that run directly adjacent to each other (or even overlapping) for some part of their lengths. But how can this be, given that we explicitly check for proximity of a street to the edges of the lot that it’s placed in? Well, that’s the problem, actually: we check for proximity to the edges of the lot it’s placed in, but we’ve just decided to extend streets in both directions past the ends of the lots they’re placed in—and we aren’t checking for proximity to the edges of those other lots that the street will pass through!

Breathing room, redux

So we’ll add an explicit check for that (as usual, omitted code is unchanged):

function getBoundingBlockAtPoint(point, options) {
	options = Object.assign({
		streetWidth: 1,
		orientation: null
	}, options);

	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >= options.streetWidth 
		   	)
		&& street.orientation != options.orientation
	);
	let parallelStreets = L.streets.filter(street => 
		street.orientation == options.orientation
	);

	let compareFunction = (a, b) => {
		if (a.orientation == "v") {
			if (a.x < b.x)
				return -1;
			if (a.x > b.x)
				return 1;
			return 0;
		} else {
			if (a.y < b.y)
				return -1;
			if (a.y > b.y)
				return 1;
			return 0;
		}
	};

	let nearestStreetLeft, nearestStreetRight, nearestStreetAbove, nearestStreetBelow;
	let blockLeft, blockTop, blockRight, blockBottom;

	if (options.orientation == "h") {
		nearestStreetLeft = crossStreets.filter(street => 
			   street.x <= point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).last;
		nearestStreetRight = crossStreets.filter(street => 
			   street.x > point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).first;

		blockLeft = nearestStreetLeft.x + nearestStreetLeft.width;
		blockRight = nearestStreetRight.x;

		nearestStreetAbove = parallelStreets.filter(street => 
			   street.x < blockRight
			&& street.x + street.length >= blockLeft
			&& street.y <= point.y
		).sort(compareFunction).last;
		nearestStreetBelow = parallelStreets.filter(street => 
			   street.x < blockRight
			&& street.x + street.length >= blockLeft
			&& street.y > point.y
		).sort(compareFunction).first;

		let spaceAbove = point.y - (nearestStreetAbove.y + nearestStreetAbove.width);
		let spaceBelow = nearestStreetBelow.y - (point.y + options.streetWidth);

		let minSpaceAbove = Math.max(L.minMonolithFootprint, 
									 Math.min(options.streetWidth, nearestStreetAbove.width || options.streetWidth) * L.streetRepulsionFactor);
		let minSpaceBelow = Math.max(L.minMonolithFootprint,
									 Math.min(options.streetWidth, nearestStreetBelow.width || options.streetWidth) * L.streetRepulsionFactor);

		if (   spaceAbove < minSpaceAbove
			|| spaceBelow < minSpaceBelow) {
			return null;
		} else {
			blockTop = nearestStreetAbove.y + nearestStreetAbove.width;
			blockBottom = nearestStreetBelow.y;
		}
	} else {
		nearestStreetAbove = crossStreets.filter(street =>
			   street.y <= point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).last;
		nearestStreetBelow = crossStreets.filter(street => 
			   street.y > point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).first;

		blockTop = nearestStreetAbove.y + nearestStreetAbove.width;
		blockBottom = nearestStreetBelow.y;

		nearestStreetLeft = parallelStreets.filter(street => 
			   street.y < blockBottom
			&& street.y + street.length >= blockTop
			&& street.x <= point.x
		).sort(compareFunction).last;
		nearestStreetRight = parallelStreets.filter(street => 
			   street.y < blockBottom
			&& street.y + street.length >= blockTop
			&& street.x > point.x
		).sort(compareFunction).first;

		let spaceLeft = point.x - (nearestStreetLeft.x + nearestStreetLeft.width);
		let spaceRight = nearestStreetRight.x - (point.x + options.streetWidth);

		let minSpaceLeft  = Math.max(L.minMonolithFootprint, 
									 Math.min(options.streetWidth, nearestStreetLeft.width  || options.streetWidth) * L.streetRepulsionFactor);
		let minSpaceRight = Math.max(L.minMonolithFootprint,
									 Math.min(options.streetWidth, nearestStreetRight.width || options.streetWidth) * L.streetRepulsionFactor);

		if (   spaceLeft  < minSpaceLeft
			|| spaceRight < minSpaceRight) {
			return null;
		} else {
			blockLeft = nearestStreetLeft.x + nearestStreetLeft.width;
			blockRight = nearestStreetRight.x;
		}
	}

	return {
		x:      blockLeft,
		y:      blockTop,
		width:  blockRight - blockLeft,
		height: blockBottom - blockTop,
		left:   blockLeft,
		right:  blockRight,
		top:    blockTop,
		bottom: blockBottom
	}
}

However, when we run this code, it seems to hang. On closer investigation, it’s actually running just fine—but because of the check that we’ve added, the algorithm will, at a certain point, start failing to find a suitable street placement (i.e., discovering that the randomly chosen point at which to attempt street placement is actually such that a street of the randomly chosen width and orientation cannot be placed there without passing impermissibly close to an edge of one or more lots) almost all the time, and finding a suitable placement more and more rarely. To illustrate this, we add a bit of debugging output:

function placeRandomStreet() {
	// … code omitted …

	if (boundingBlock == null) {
		console.log("Bounding block is null!");
		return true;
	}

	// … code omitted …

	console.log(`Placed a street (${L.streets.length} streets total). ${L.lots.length} lots remain.`);

	return true;
}

And this is what we see after less than a minute of runtime:

Figure 13. (Click to zoom in.)

If we wait for this to complete, we’ll be here all day…

Stopping halfway

Well, what happens if we stop the process after placing, let’s say, 4,000 streets? (The number is obviously chosen in an ad-hoc manner, and that won’t do for the actual implementation, but we’re just experimenting here.) The code still takes uncomfortably long to get even that far (around 15 seconds—much too long for a procgen like this), but:

Figure 14. (Click to zoom in.)

This seems fine. Of course most of the lots are bigger than we need them to be, but that is fixable, with the subdivision technique we’ve already used. And so:

Figure 15. (Click to zoom in.)

Nice! This is basically what we’re looking for. We’ve certainly solved our problem with the lack of X-intersections. The street clumping problem remains, but we’ll get to that later. First, though: how do we fix this excessive runtime? And how can we pick a stopping point in a less ad-hoc and arbitrary way than simply picking a street count? (Which would be map-size-dependent, anyhow.)

Roll to give up

We can use probabilistic stopping. That is: whenever we pick a random point (and random street width and orientation) and fail to place a street there (because of impermissible proximity to the edges of one or more of the lots the street would cross, if extended as far as it can be), we will roll a die (a 10,000-sized die, let’s say). If the die comes up anything but 1, we’ll keep trying; if it comes up 1, we’ll give up, and declare that random street placement is concluded.³ (At this point, we subdivide all remaining too-large lots with streets of width 1, as before.)

The modification to the code is trivial:

L = {
	//	… other configuration fields omitted …

	keepTryingHowHard: 10000
};

function placeRandomStreet() {
	// … code omitted …

	if (boundingBlock == null) {
		return (rollDie(L.keepTryingHowHard) != 1);
	}

	// … code omitted …
}

Figure 16. (Click to zoom in.)

Cool. Now the code finishes in couple of seconds at most—mission accomplished.

Cornstarch added to prevent

We’re very close to perfection now, but let’s see if we can solve that “street clumping” problem. Recall that this was caused by the fact that we are selecting a random lot to place a street in, which means that if the left half of the map has 10 lots and the right half has one big lot, then new streets are 10 times more likely to be placed on the left half of the map than on the right half, which results in the left half having even more lots and thus being even more likely to have new streets placed there… etc.

Well, one obvious solution is to instead select a point at random from a uniform distribution of all grid locations. (We will, of course, have to check that the point we’ve selected isn’t on a street instead of being within any lot, but that is easy enough.) Thus (omitted code unchanged, as usual):

function getRandomGridPoint() {
	return {
		x: rollDie(L.gridWidth) - 1,
		y: rollDie(L.gridHeight) - 1
	};
}

function pointIsOnStreet(point, street) {
	if (street.orientation == "h") {
		return (   point.x >= street.x
				&& point.x < street.x + street.length
				&& point.y >= street.y
				&& point.y < street.y + street.width);
	} else {
		return (   point.x >= street.x
				&& point.x < street.x + street.width
				&& point.y >= street.y
				&& point.y < street.y + street.length);
	}
}

function getBoundingBlockAtPoint(point, options) {
	options = Object.assign({
		streetWidth: 1,
		orientation: null
	}, options);

	if (L.streets.findIndex(street => pointIsOnStreet(point, street)) !== -1)
		return null;
	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >= options.streetWidth 
		   	)
		&& street.orientation != options.orientation
	);
	let parallelStreets = L.streets.filter(street => 
		street.orientation == options.orientation
	);

	let compareFunction = (a, b) => {
		if (a.orientation == "v") {
			if (a.x < b.x)
				return -1;
			if (a.x > b.x)
				return 1;
			return 0;
		} else {
			if (a.y < b.y)
				return -1;
			if (a.y > b.y)
				return 1;
			return 0;
		}
	};

	let nearestStreetLeft, nearestStreetRight, nearestStreetAbove, nearestStreetBelow;
	let blockLeft, blockTop, blockRight, blockBottom;

	if (options.orientation == "h") {
		nearestStreetLeft = crossStreets.filter(street => 
			   street.x <= point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).last;
		nearestStreetRight = crossStreets.filter(street => 
			   street.x > point.x
			&& street.y <= point.y
			&& street.y + street.length >= point.y
		).sort(compareFunction).first;

		blockLeft = nearestStreetLeft.x + nearestStreetLeft.width;
		blockRight = nearestStreetRight.x;

		nearestStreetAbove = parallelStreets.filter(street => 
			   street.x < blockRight
			&& street.x + street.length >= blockLeft
			&& street.y <= point.y
		).sort(compareFunction).last;
		nearestStreetBelow = parallelStreets.filter(street => 
			   street.x < blockRight
			&& street.x + street.length >= blockLeft
			&& street.y > point.y
		).sort(compareFunction).first;

		let spaceAbove = point.y - (nearestStreetAbove.y + nearestStreetAbove.width);
		let spaceBelow = nearestStreetBelow.y - (point.y + options.streetWidth);

		let minSpaceAbove = Math.max(L.minMonolithFootprint, 
									 Math.min(options.streetWidth, nearestStreetAbove.width || options.streetWidth) * L.streetRepulsionFactor);
		let minSpaceBelow = Math.max(L.minMonolithFootprint,
									 Math.min(options.streetWidth, nearestStreetBelow.width || options.streetWidth) * L.streetRepulsionFactor);

		if (   spaceAbove < minSpaceAbove
			|| spaceBelow < minSpaceBelow) {
			return null;
		} else {
			blockTop = nearestStreetAbove.y + nearestStreetAbove.width;
			blockBottom = nearestStreetBelow.y;
		}
	} else {
		nearestStreetAbove = crossStreets.filter(street =>
			   street.y <= point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).last;
		nearestStreetBelow = crossStreets.filter(street => 
			   street.y > point.y
			&& street.x <= point.x
			&& street.x + street.length >= point.x
		).sort(compareFunction).first;

		blockTop = nearestStreetAbove.y + nearestStreetAbove.width;
		blockBottom = nearestStreetBelow.y;

		nearestStreetLeft = parallelStreets.filter(street => 
			   street.y < blockBottom
			&& street.y + street.length >= blockTop
			&& street.x <= point.x
		).sort(compareFunction).last;
		nearestStreetRight = parallelStreets.filter(street => 
			   street.y < blockBottom
			&& street.y + street.length >= blockTop
			&& street.x > point.x
		).sort(compareFunction).first;

		let spaceLeft = point.x - (nearestStreetLeft.x + nearestStreetLeft.width);
		let spaceRight = nearestStreetRight.x - (point.x + options.streetWidth);

		let minSpaceLeft  = Math.max(L.minMonolithFootprint, 
									 Math.min(options.streetWidth, nearestStreetLeft.width  || options.streetWidth) * L.streetRepulsionFactor);
		let minSpaceRight = Math.max(L.minMonolithFootprint,
									 Math.min(options.streetWidth, nearestStreetRight.width || options.streetWidth) * L.streetRepulsionFactor);

		if (   spaceLeft  < minSpaceLeft
			|| spaceRight < minSpaceRight) {
			return null;
		} else {
			blockLeft = nearestStreetLeft.x + nearestStreetLeft.width;
			blockRight = nearestStreetRight.x;
		}
	}

	return {
		x:      blockLeft,
		y:      blockTop,
		width:  blockRight - blockLeft,
		height: blockBottom - blockTop,
		left:   blockLeft,
		right:  blockRight,
		top:    blockTop,
		bottom: blockBottom
	}
}

Figure 17. (Click to zoom in.)

Excellent. The street clumping problem has been banished. We have the result we want.

Optional Manhattanization

One final thought: in our current implementation, we allow streets to cut across existing streets that are narrower (than the street being placed). What if we tweaked this condition? The relevant part of the code is this, in the getBoundingBlockAtPoint() function:

	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >= options.streetWidth 
		   	)
		&& street.orientation != options.orientation
	);

Here’s the kind of thing we get if we allow streets to cut across existing streets that are narrower or as narrow:

	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >  options.streetWidth 
		   	)
		&& street.orientation != options.orientation
	);

Figure 18. (Click to zoom in.)

And here’s what we get if we allow streets to cut across existing streets that are at most twice as wide:

	let crossStreets = L.streets.filter(street => 
		   (   street.width == 0
		    || street.width >  options.streetWidth * 2
		   	)
		&& street.orientation != options.orientation
	);

Figure 19. (Click to zoom in.)

Probably this isn’t very useful, but the option is there, if we want it.

(If we allow streets to cut across existing streets of any width, we simply get figure 4, of course.)

The algorithm

It may seem otherwise from the lengthy discussion thus far, but this really is a simple approach. (One might even call it “simplistic”. There isn’t anything very clever about this algorithm, and there’s no particular reason to be impressed by it. But it works well.)

1. Start trying to place streets of random width and orientation at random points on the grid, checking to make sure they don’t run too close to any other streets. Each time you fail to place a street, roll a big die; if you roll a 1, give up and go to the next step.
2. Find any lots (i.e., blocks of un-divided space) that are bigger than the minimum lot size, and divide them into two lots (at a random split point, down the shorter axis of the lot). Keep doing this until there are no too-big lots remaining.
3. You’re done! Render to the output format, display, save, whatever.

Implementation details

How should we save these maps, by the way? I’ve chosen SVG for the output format, because it’s widely supported, editable, usable for other purposes (see the next part of this series), and convertible into bitmap format, if need be. I see no compelling arguments for doing it in any other way.

There is one small detail of the output format which is a bit less obvious. What exactly should be represented? “Just monoliths” is one possible answer; “just streets” is another; “both” is a third. (Note that this question arises only because we’re using a vector file format; in a bitmap image, these three cases are completely indistinguishable given the constraints we’ve imposed on the generated map.)

I think that monoliths have to be represented (because it is otherwise unnecessarily tedious to derive the set of monolith coordinates from the set of street parameters), but whether streets also need to be represented is an open question, the answer to which depends on the use to which the SVG map file will be put. I have opted not to include streets by default, to reduce SVG file complexity (SVGs with many elements take longer to render in browsers or other viewing programs), but you can override that default by passing true to the saveSVG() function.

The demo

You can try out the generator for yourself:

https://dnd.obormot.net/lacc/

Note that there’s no GUI. To generate a new map, simply reload the page. To save the generated map, open the JavaScript console and run the saveSVG() function. (Pass true to said function if you want streets to be included as distinct elements in the SVG; by default, only monoliths will be included, with streets left implicit as the negative space between monoliths.)

The code

Download the code (zip file). (Everything in the package is MIT licensed.)

The scenario:

In the depths of the Plane of Shadow stands Lacc, an ancient, unimaginably vast city inhabited by restless shades and creatures of darkness. This City of Monoliths consumes entire worlds, incorporating each world into itself as the monoliths that give Lacc its nickname grind their way across the landscape, expanding like a growing ink-stain upon a planet’s surface.

The important question, of course, is: how should I model this process mathematically?

The scenario described above comes from an adventure module called “Gates of Oblivion” (by Alec Austin), published in Dungeon magazine #136. The module states that “The area consumed by Lacc expands at a rate of half a mile per hour”. This is clear enough, but: (a) it’s entirely the wrong sort of rate function for the needs of the adventure; (b) it’s much too arbitrary; and (c) it’s much too straightforward and thus boring.

What is the geometry of the Plane of Shadow?

Most planes (certainly including the Inner Planes) are said to be infinite in all directions (cf. the Manual of the Planes)—but how many directions is “all”? While considering this, I recalled certain suggestions (e.g. this blog post, Dragon magazine #8, #17, #38, etc.) that the planes exist in four spatial dimensions. This makes sense: if there’s only one Plane of Shadow, say, for all the Material Planes in existence (and such is indeed the canonical depiction of the planes in D&D), there will hardly be enough of it to contain everything that it would need to have (i.e., shadow reflections of Material Plane locations and inhabitants, for multiple—possibly infinitely many—Material Planes), if its dimensionality is no greater than that of a Material Plane.

This gave me the idea of modeling the manifestation of the City of Monoliths upon the Prime Material Plane as an intrusion of a four-dimensional object into a three-dimensional space. In this model, Lacc exists in four spatial dimensions, of which three are “lateral” (“north”, “south”, “east”, “west”, “kata”, “ana”) and one is the usual up–down. An incursion of Lacc onto the planet where our player characters reside will have the shape of an expanding hypersphere in four-dimensional space, the three-dimensional surface of which contains two “lateral” spatial dimensions and the one “vertical” dimension; at the point of contact with the PCs’ three-dimensional space, the contents of this surface will “flow” out into that space, the two “lateral” spatial dimensions of Lacc expanding onto the planet’s surface, and constituting the growing zone of darkness and inexorably advancing stone monoliths that the world’s inhabitants behold.

Consider first the one-dimension-lower analogue of the situation. We have two parallel planes (2D spaces), call them {$M$} and {$L$}, separated by a distance of {$d$} in the three-dimensional space within which they’re both embedded (figure 1); these are our analogues of the Prime Material Plane, and the city of Lacc in the Plane of Shadow, respectively. In {$M$} is a circle {$C_{M}$}; this is our analogue of a three-dimensional planet. (Note that the exterior of a circle is a finite one-dimensional space, just as the exterior of a sphere is a finite two-dimensional space.)

Figure 1.

At a point {$P_{M}$} on {$C_{M}$}, we construct a line, perpendicular to plane {$M$}; designate the point where this line intersects plane {$L$} as {$P_{L}$} (figure 2).

Figure 2. The length of {$\overline{P_{M}P_{L}}$} is equal to {$d$}.

Now we construct a sphere {$S$}, centered at {$P_{L}$} (figure 3). The radius {$r_{S}$} of sphere {$S$} begins at 0 and increases as time passes, the increase going as the square root of time {$t$} (with a constant growth rate coefficient {$k$}). (Why the square root? We’ll come to that. Note that this naturally means that the surface area of {$S$}—which is proportional to the square of the radius—will increase linearly with {$t$}.)

Figure 3. Sphere {$S$} at some time {$0<t<t_{M}$}; {$0<r_{S}<d$}.

At some {$t_{M}$}, the radius {$r_{S}$} of sphere S will be equal to the distance {$d$} that separates planes {$M$} and {$L$}. At this time, {$S$} will be tangent to {$M$} (figure 4). The point of contact will of course be {$P_{M}$} (which, recall, is a point on the exterior of the circle {$C_{M}$} in plane {$M$}).

Figure 4. Sphere {$S$} at {$t=t_{M}$}; {$r_{S}=d$}.

As time continues to pass and {$r_{S}$} keeps increasing, the sphere {$S$} will intersect plane {$M$}, which will cut off a spherical cap {$\mathit{CAP}_{S}$} (figures 5 and 6).

Figure 5. Sphere {$S$} at {$t_{M}<t<t_{total\ doom}$}; {$r_{S}>d$}; {$A(\mathit{CAP}_{S})>0$}; {$0<r_{C_{S}}<2r_{C_{M}}$}.

The shape of the intersection of {$S$} with {$M$} is of course a circle, but we are not interested in that. As noted before, the contents of the surface of the expanding sphere (or hypersphere, in the actual model) should “flow” into the Material Plane. Thus what we’re actually interested in is the surface area of {$\mathit{CAP}_{S}$}. We will map that area onto plane {$M$} by drawing a circle {$C_{S}$}, centered at point {$P_{M}$}, with area equal to the surface area {$A(\mathit{CAP}_{S})$} (figure 7).

Figure 6. {$\mathit{CAP}_{S}$}.

Figure 7. Orthogonal view onto plane {$M$}. Note that the smaller of the two circles centered at {$P_{M}$} represents the intersection of {$S$} with {$M$} (i.e., the base of {$\mathit{CAP}_{S}$}), and is not what we are interested in. Rather, we are concerned with {$C_{S}$}, the circle with area equal to {$A(\mathit{CAP}_{S})$}.

As {$t$} increases, {$A(\mathit{CAP}_{S})$}, and thus the area {$A(C_{S})$} of circle {$C_{S}$}, will increase approximately linearly with time as well (after {$t_{M}$}, that is; prior to {$t_{M}$}, {$A(\mathit{CAP}_{S})$} is of course zero); the radius {$r_{C_{S}}$} of {$C_{S}$} will increase approximately as the square root of t. As {$C_{S}$} grows (remember that it is centered on point {$P_{M}$} on the exterior of {$C_{M}$}), it will encompass an increasingly large sector of the circumference of {$C_{M}$} (figure 8), until a time {$t_{total\ doom}$} is reached when {$C_{S}$} fully contains {$C_{M}$}. (As {$C_{M}$} is our two-dimensional analogue of a planet, its circumference is the one-dimensional analogue of the planet’s surface.)

Figure 8. One-half of the arc of {$C_{M}$} which is encompassed by {$C_{S}$} is {$l_{semiarc}$}. This is the arc of {$C_{M}$} which is cut off by a chord with one endpoint at {$P_{M}$} and length equal to {$r_{C_{S}}$}.

We can now derive the formula for the arc-length of the encompassed sector {$C_{M}$}.

Radius of the expanding sphere {$S$}:

{$$ r_{S}=k\sqrt{t} $$}

Surface area of the spherical cap {$\mathit{CAP}_{S}$}:

{$$ A(\mathit{CAP}_{S})=2πr_{S}(r_{S}-d) $$}

(This value, and all subsequent equations that depend on it, will be zero when {$r_{S}\leq d$}, i.e. when {$S$} has not yet grown large enough to intersect {$M$}.)

Radius of circle with area equal to {$A(\mathit{CAP}_{S})$}:

{$$ r_{C_{S}}=\sqrt{\frac{A(\mathit{CAP}_{S})}{2π}} $$}

Arc-length of one-half of the arc of {$C_{M}$} which is contained within {$C_{S}$}:

{$$ l_{semiarc}=2r_{C_{M}}\cdot asin\left(\frac{r_{C_{S}}}{2r_{C_{M}}}\right) $$}

Substituting and simplifying:

{$$ l_{semiarc}=2r_{C_{M}}\cdot asin\left(\frac{\sqrt{k\sqrt{t}(k\sqrt{t}-d)}}{2r_{C_{M}}}\right) $$}

We can see that the value of {$t_{total\ doom}$} (which will occur when {$l_{semiarc}$} equals one-half the circumference of {$C_{M}$}) naturally depends on three variables:

• the planar separation distance {$d$} between {$M$} and {$L$}
• the growth rate coefficient {$k$} of {$r_{S}$} (a constant factor applied to the equation which relates {$r_{S}$} to {$t$})
• the radius {$r_{C_{M}}$} of circle {$C_{M}$} (which is the 2-dimensional analogue of the PCs’ home planet)

So that was the simplified (one-dimension-lower) version. Now we must add one dimension to the above considerations, which, unsurprisingly, makes our task rather more tricky. (There will be fewer diagrams in this part, as I do not have an easy way to depict four-dimensional spaces in a two-dimensional medium.)

We have two parallel three-dimensional spaces, again called {$M$} and {$L$}, separated by a distance of {$d$} in the four-dimensional space within which they’re both embedded; these are the Prime Material Plane, and the city of Lacc in the Plane of Shadow. In {$M$} is a sphere {$S_{M}$} (the world of the player characters). At a point {$P_{M}$} on {$S_{M}$}, we construct a line, perpendicular to space {$M$}; designate the point where this line intersects space {$L$} as {$P_{L}$}. Now we construct a hypersphere (specifically, a 3-sphere) {$H$}, centered at {$P_{L}$}. The radius {$r_{H}$} of hypersphere {$H$} begins at 0 and increases as time passes, the increase going as the cube root of time {$t$} (with a constant growth rate coefficient {$k$}). (This naturally means that the three-dimensional surface area of H will increase linearly with t.)

At some point {$t_{M}$}, the radius {$r_{H}$} of hypersphere {$H$} will be equal to the distance d that separates spaces {$M$} and {$L$}. At this time, {$H$} will be tangent to {$M$}. The point of contact will of course be {$P_{M}$} (which, recall again, is a point on the surface of the sphere {$S_{M}$} in space {$M$}). As time continues to pass and {$r_{H}$} keeps increasing, the hypersphere {$H$} will intersect space {$M$}, which will cut off a hyperspherical cap {$\mathit{CAP}_{H}$}.

The shape of the intersection of {$H$} with {$M$} is of course a sphere, but once again that does not interest us; in our scenario, the contents of the three-dimensional surface of the hypersphere should flow into the Material Plane (i.e., space {$M$}). Thus what interests us is the (three-dimensional) surface area of {$\mathit{CAP}_{H}$}. We will map that area onto space {$M$} by drawing a sphere {$S_{H}$}, centered at point {$P_{M}$}, with a volume {$V(S_{H})$} equal to the (3D) surface area {$A(\mathit{CAP}_{H})$}. As t increases, {$A(\mathit{CAP}_{H})$}, and thus the volume {$V(S_{H})$} of sphere {$S_{H}$}, will increase approximately linearly with time as well (but, again, only after {$t_{M}$}, prior to which {$A(\mathit{CAP}_{H})$} is zero); the radius {$r_{S_{H}}$} of {$S_{H}$} will increase approximately as the cube root of t. As {$S_{H}$} (which is centered on point {$P_{M}$} on the surface of {$S_{M}$}) grows, it will encompass an increasingly large (circular) sector of the surface of {$S_{M}$}, until a time {$t_{total\ doom}$} is reached when {$S_{H}$} fully contains {$S_{M}$} (i.e., totally encompasses the planet).

So, in order to determine the rate of Lacc’s expansion across the surface of the PCs’ world, we need to determine {$r_{sector}$}, the arc-radius of the circular sector of {$S_{M}$} which is subsumed by {$S_{H}$} at any given time {$t$}. This depends on the radius of the sphere {$S_{H}$}, which we can trivially determine from the volume {$V(S_{H})$}; and that, in turn, is stipulated to be equal to the (three-dimensional) surface area {$A(\mathit{CAP}_{H})$}.

Determining the (3D) surface area of a hyperspherical cap turns out to be a tricky problem, which seems to have been solved in closed form only surprisingly recently. The most recent (and, indeed, only) source I was able to find is a paper called “Concise Formulas for the Area and Volume of a Hyperspherical Cap”, by Shengqiao Li, published in 2011 in the Asian Journal of Mathematics and Statistics. The formula which Li gives for the surface area of a hyperspherical cap makes use of a function called the regularized incomplete beta function:

{$$ A(\mathit{CAP}_{H})=\frac{1}{2}\cdot A(H)\cdot I_{sin^{2}\phi}\left(\frac{n-1}{2},\frac{1}{2}\right) $$}

(Note that {$\phi$} here is one-half the arc angle of {$\mathit{CAP}_{H}$}; this is also known as the colatitude angle.)

As used here, this function takes as its one parameter the number of dimensions {$n$} of the sphere whose surface area is to be computed; in our case this is 3 (remember that a circle is a 1-sphere; a regular sphere, e.g. a planet or a basketball, is a 2-sphere; a hypersphere, i.e. a sphere in four dimensions, is a 3-sphere). Li helpfully gives equivalent forms for this function, for integer {$n\in [1,4]$}. For {$n=3$}, the formula thus becomes:

{$$ A(\mathit{CAP}_{H})=\frac{1}{2}\cdot A(H)\cdot \frac{2\phi-sin(2\phi)}{π} $$}

We can now derive the formula which gives us {$r_{sector}$} (the arc-radius on the planet’s surface of the expanding zone of Lacc’s incursion into the PCs’ world) as a function of {$t$} (time in days).

Radius of the expanding hypersphere {$H$}:

{$$ r_{H}=k\sqrt[3]{t} $$}

Surface area (3D) of {$H$}:

{$$ A(H)=2π^{2}r_{H}^{3} $$}

Colatitude angle of hyperspherical cap {$\mathit{CAP}_{H}$}:

{$$ \phi=acos\left(\frac{d}{r_{H}}\right) $$}

Surface area (3D) of hyperspherical cap {$\mathit{CAP}_{H}$}:

{$$ A(\mathit{CAP}_{H})=\frac{1}{2}\cdot A(H)\cdot (\frac{2\phi-sin(2\phi)}{π}) $$}

Radius of sphere with volume equal to {$A(\mathit{CAP}_{H})$}:

{$$ r_{S_{H}}=\sqrt[3]{\frac{3}{4π}\cdot A(\mathit{CAP}_{H})} $$}

Arc-radius of the circle on the surface of {$S_{M}$} encompassed by {$S_{H}$}:

{$$ r_{sector}=2r_{S_{M}}\cdot asin\left(\frac{r_{S_{H}}}{2r_{S_{M}}}\right) $$}

Substituting and simplifying:

{$$ r_{sector}=2r_{S_{M}}\cdot asin\left(\frac{\sqrt[3]{\frac{4}{3π}\cdot A(\mathit{CAP}_{H})}}{2r_{S_{M}}}\right) $$}

{$$ =2r_{S_{M}}\cdot asin\left(\frac{\sqrt[3]{\frac{2}{3π}\cdot A(H)\cdot (\frac{2\phi-sin(2\phi)}{π})}}{2r_{S_{M}}}\right) $$}

{$$ =2r_{S_{M}}\cdot asin\left(\frac{\sqrt[3]{\frac{2}{3π^2}\cdot A(H)\cdot \left(2\cdot acos\left(\frac{d}{r_{H}}\right)-sin\left(2\cdot acos\left(\frac{d}{r_{H}}\right)\right)\right)}}{2r_{S_{M}}}\right) $$}

{$$ =2r_{S_{M}}\cdot asin\left(\frac{\sqrt[3]{\frac{4}{3}r_{H}^{3}\cdot \left(2\cdot acos\left(\frac{d}{r_{H}}\right)-sin\left(2\cdot acos\left(\frac{d}{r_{H}}\right)\right)\right)}}{2r_{S_{M}}}\right) $$}

{$$ =2r_{S_{M}}\cdot asin\left(\frac{k}{2r_{S_{M}}}\cdot \sqrt[3]{\frac{4}{3}t\cdot \left(2\cdot acos\left(\frac{d}{k\sqrt[3]{t}}\right)-sin\left(2\cdot acos\left(\frac{d}{k\sqrt[3]{t}}\right)\right)\right)}\right) $$}

Once again the value of {$t_{total\ doom}$} (and, more generally, the relationship of the time {$t$} to the radius {$r_{sector}$} of the sector of {$S_{M}$} encompassed by the growing sphere {$S_{H}$} of Lacc’s incursion into the Prime Material Plane) depends on three variables:

• the spatial separation distance {$d$} between {$M$} and {$L$}
• the growth rate coefficient {$k$} of {$r_{H}$}
• the radius {$r_{S_{M}}$} of sphere {$S_{M}$} (i.e., of the PCs’ home planet)

It is customary to assume that the worlds of most D&D settings are approximately Earth-like in basic characteristics, such as size, mass, etc.¹ We will therefore set {$r_{S_{M}}$} to match that of Earth: 3959 miles.

That leaves the rate of growth {$k$} and the spatial separation distance {$d$}. These are essentially free variables, in that they are not constrained by any aspect of the model we’ve described so far, nor is there (yet) any obvious reason why either of them should take on any particular value rather than any other. This leaves us free to choose the values of both variables on the basis of adventure design considerations.

As noted previously, we would like to give the PCs a reasonable but not excessive amount of time (namely, somewhere from a week to a month, probably closer to the latter; let’s now make a concrete choice, and name three weeks as our critical time frame) to complete the adventure. Note that this period starts not at {$t=0$}, but rather at {$t=t_{M}$}, i.e. the time at which the hypersphere radius {$r_{H}$} is just large enough for the hypersphere {$H$} to make contact with space {$M$} (the Prime Material Plane). Likewise, the end of the critical period (i.e., the time at which, if the PCs have not defeated Tenaris Xin, they fail in their quest and their world is forfeit) occurs not at {$t=t_{total\ doom}$} (the hypothetical—and, as it turns out, irrelevant—time at which the sphere {$S_{H}$} would encompass the entirety of {$S_{M}$}); rather, it’s the moment at which Xin completes his ritual (whereupon the PCs’ world is absorbed into Lacc immediately).

Obviously, we may stipulate Xin’s ritual to take however long we wish it to take. If we say it takes three weeks to complete, then that’s how long it takes. The task is to make the ritual’s casting time (and, ideally, every other detail of the adventure setup) seem to be non-arbitrary.² There’s also another, related, design goal: to communicate to the players (i.e., to give their characters a way to intuit) that they are facing a concrete deadline (and what the time scale of that deadline is).

Here is how we will do it. In “Gates of Oblivion”, the means by which Lacc consumes a world is linked to three magical gates (the Colorless Gate, the Empty Gate, and the Hollow Gate); these are arranged in an equilateral triangle (figure 9), with Tenaris Xin’s tower at the center, equidistant from all three. Each Gate is exactly 16 miles from Xin’s tower. (This results in a triangle with sides approximately 27.7 miles long.)

Figure 9. The three magical Gates and the tower of Tenaris Xin, in Lacc, the City of Monoliths.

We are now going to slightly modify the setup described above. Instead of a single point {$P_{M}$} on the planet’s surface, we identify three points, arranged in an equilateral triangle, 27.7 miles to the side. From each of these points, we will construct a line perpendicular to {$M$}, then a hypersphere with center at the point where the line intersects {$L$}, etc., all as described previously. Thus we will have not one but three expanding zones of darkness (figure 10), as Lacc will make contact with the world of the PCs at three points (the vertices of the triangle).

Figure 10. Not one, but three distinct intrusion zones, located somewhere on the surface of the player characters’ home world.

Furthermore, we will now specify the spatial separation distance {$d$} to be 16 miles (matching the distance from each of the three Gates to the tower of Tenaris Xin).

This has several results. First, it naturally creates a temporal Schelling point which the players can identify as a plausible candidate for when something might happen: namely, the moment when the three expanding zones meet (figure 11).³ (It does not take a great leap of intuition to suspect that this will be a bad thing.) This is the hint to the players (and the PCs) that there’s a much closer deadline than merely “when the intrusion zone expands to encompass the whole world” (which will quite clearly be many months or even years away, given the observed expansion rate of the intrusion zones).

Figure 11. The expansion of the three intrusion zones brings them into contact at {$t=t_{zone\ contact}$}, when {$r_{sector}$} is equal to one-half the distance between the centers of the three zones (and also, necessarily, one-half the distance between the three Gates in Lacc).

Second, it allows the players to identify parallels between elements of the setup, which both creates the perception of a logically connected system and offers hints that point the PCs to the key locations which they must visit in order to gain more information about Tenaris Xin’s plans and, thereby, to successfully complete the adventure. That is: the center points of the intrusion zones form a triangle 16 miles from a center point. The spatial separation distance (which the PCs will have to cross in their journey to the heart of Lacc; see below) is likewise 16 miles; noticing this will give the PCs a hint that this value is somehow important. When the PCs arrive in the Plane of Shadow, they can notice the correspondence of the location of one of the Gates to the center point of the intrusion zone in their world, and intuit that the two other Gates exist and that they are important. If they think to travel to the center point of the triangle formed by the three Gates (which again is 16 miles away from each Gate), they will arrive at Xin’s tower.⁴

(Needless to say, none of these hints or deductions should be the only avenue by which the players can reach any of the aforementioned conclusions or learn any of the information I’ve described. In accordance with the three clue rule, there should be multiple hints or clues pointing the players toward these nodes in the scenario structure. Enumerating the rest of that scenario structure is beyond the scope of this post. Here it is important to notice only that carefully planning out the geometry of Lacc’s incursion allows us to use that very geometry as one source of clues for the players. This rewards players who pay attention to such details, encourages careful thought, and contributes greatly to the sense of the adventure’s events as coherent, logical, predictable, and amenable to understanding.)

Having specified the planetary radius {$r_{S_{M}}$} and the spatial separation distance {$d$}, it now remains for us only to pick the growth rate coefficient {$k$}. We will select a value of {$k$} that results in a period of exactly three weeks between {$t_{M}$} (the time at which the three hyperspheres of Lacc’s intrusion zones first make contact with the Prime Material Plane, and the beginning of the adventure) and {$t_{zone\ contact}$}³ (the time when the three expanding intrusion zones on the surface of the PCs’ world meet at three points of tangency), which we have decided is the moment at which Tenaris Xin completes his ritual, and the PCs’ world is permanently absorbed into the City of Monoliths. This value is 5.36.⁵

The formula we previously derived for the arc-radius of each of the three intrusion zones is:

{$$ r_{sector}=2r_{S_{M}}\cdot asin\left(\frac{k}{2r_{S_{M}}}\cdot \sqrt[3]{\frac{4}{3}t\cdot \left(2\cdot acos\left(\frac{d}{k\sqrt[3]{t}}\right)-sin\left(2\cdot acos\left(\frac{d}{k\sqrt[3]{t}}\right)\right)\right)}\right) $$}

And the values we’ve chosen for our three key variables are:

• {$r_{S_{M}}$} (the radius of sphere {$S_{M}$}, the PCs’ home planet): 3959 miles
• {$d$} (the spatial separation distance between {$M$} and {$L$}): 16 miles
• {$k$} (the growth rate coefficient of the hypersphere radii {$r_{H}$}): 5.36

Substituting those values, we get:

{$$ r_{sector}=7918\cdot asin\left(\frac{5.36}{7918}\cdot \sqrt[3]{\frac{4}{3}t\cdot \left(2\cdot acos\left(\frac{16}{5.36\cdot \sqrt[3]{t}}\right)-sin\left(2\cdot acos\left(\frac{16}{5.36\cdot \sqrt[3]{t}}\right)\right)\right)}\right) $$}

And the resulting values of {$r_{sector}$}:

Figure 13. Lacc intrusion zone radius in miles as a function of time in days since Tenaris Xin begins his ritual.

Rows in bold are key days. Day 27 is {$t_{M}$}, when Lacc first makes contact with the PCs’ home world, and the three intrusion zones appear (27.7 miles apart from one another) somewhere on the world’s surface (growing to a radius of 1.9 miles within that first day). Day 48 is {$t_{zone\ contact}$}, when the three intrusion zones first touch one another, and begin to merge; this is the first of the two possible endpoints for the adventure. Day 55 is {$t_{zone\ merge}$}, at which point no gap remains between the three intrusion zones; this is the second possible endpoint for the adventure. (The DM may select one of the endpoint dates in advance, or hold off the decision until later in the adventure; needless to say, in the latter case, he should be careful not to provide any hints which identify one of the dates as the endpoint.)

By the way, what are we to make of the period prior to day 27? (This is the period when the hyperspheres {$H$} are expanding but have not yet reached {$M$}, the Prime Material Plane; so there are as yet no intrusion zones on the surface of the PCs’ world, i.e. {$r_{sector}$} is zero.) We may suppose that after selecting a world for assimilation into Lacc, Tenaris Xin begins an almost-month-long process of magical preparation, during which time the City of Monoliths begins “reaching” across the interplanar distances toward the Prime Material World of the player characters. It is reasonable to assume that there is no feasible way for the PCs (or anyone else on their world) to know about this process prior to {$t_{M}$} (day 27). However, if the DM wishes to give the players a hint of what’s to come (e.g. if using this adventure in a larger campaign), he may have signs and portents manifest during this time period (visions experienced by oracles, for example, or warnings from the gods, or strange observations recorded by scholars of the arcane who study the lore of the planes, or other things of this nature).

(Incidentally, what would be the value of {$t_{total\ doom}$} given the values we’ve selected for our key variables? That is, how long would it take for Lacc to fully engulf the PCs’ home world in the absence of the ritual (i.e. if the hyperdimensional model described above were applied to the adventure as written)? We are looking for the lowest value of {$t$} that yields an {$r_{sector}$} equal to or greater than one-half the circumference of {$S_{M}$} (that being {$πr_{S_{M}}$}, i.e. ~12,437.6 miles). This value happens to be 772,797,939 days, or approximately 2,117,254 years.)

Finally, do we now have a non-arbitrary answer for where on the surface of the PCs’ world Lacc’s intrusion zones should be located? Yes: from Tenaris Xin’s perspective, Lacc should always make contact with a target planet in some location as remote as possible from civilization, to minimize the chance that any powerful inhabitants of that world (i.e., high-level characters such as the PCs, and/or any other entities likely to possess the capability to stop Xin’s plans) will discover the intrusion zones in time to learn their nature, reach Xin’s tower, and interrupt his ritual. (Determining what other measures Xin might take to minimize the chance of being discovered and interrupted in time, as well as the details of how the PCs will, despite Xin’s plans, learn of Lacc’s incursion before it’s too late—as indeed they must, or else the adventure can’t take place—is left as an exercise for the DM.)

1 See, e.g., Concordance of Arcane Space from the Spelljammer boxed set, which places Oerth, Krynn, Toril, etc. in the same celestial body size category, drawing no distinctions between them. Exceptions do exist, such as Mystara (the planet on which the “Known World” campaign setting of D&D Basic is located), which features a significantly smaller size and hollow interior. (Of course, players in the Known World may never even realize the existence of these major structural differences, due to the “world shield”—an internal layer of ultra-dense material; perhaps neutronium?—that, among its other effects, provides sufficient mass to bring Mystara up to Earth-normal gravity.) ⇑

2 “Seem” is really the key word here. This is not an idea original to me (I recall first seeing the formulation I give here in a social media post which I have long since lost the link to), but: when creating explanations for whatever the player characters encounter, you only need to go two levels deep. That is, if the players ask why something is the way that it is, they should be able to discover an explanation; and if they ask why that is the way that it is, they should be able to discover an explanation for that, too; and at that point, they will not keep asking, because you will have successfully created the impression that there’s an explanation for everything. Furthermore, if you then, e.g., tie the explanation for the third thing back to the first thing, you have created a complete system which can support explanations of arbitrary depth.

(One can, of course, always ask “but why is this whole system the way that it is”, but given that the same question can be asked just as easily of the real world, it’s unlikely that the lack of an in-world answer will detract from verisimilitude and immersion. If the players do, after all, ask the question, Morgenbesser’s reply should suffice.) ⇑

3 Actually, if the players consider the matter carefully, they will realize that there are two uniquely identifiable moments here. One—call it {$t_{zone\ contact}$} (figure 11)—is the moment when the three expanding zones come into contact, i.e. the moment at which the three subsumed circular sectors of the planet’s surface are tangent to each other. This will occur when the arc-radii of the subsumed surface sectors are equal to one-half the length of the sides of the equilateral triangle formed by the points of contact, i.e. ~13.86 miles. The other—call it {$t_{zone\ merge}$} (figure 12)—is the moment when there is no longer any gap in the middle of the three zones; this will occur when the arc-radii of the subsumed surface sectors are equal to the distance of a vertex of the triangle from the triangle’s center point, i.e. 16 miles.

Figure 12. The three intrusion zones expand far enough to fully merge (leaving no gap in the middle between them) at {$t=t_{zone\ merge}$}, when {$r_{sector}$} is equal to the distance from the center of each zone to the center of the triangle (which is, necessarily, also the distance from each of the Gates to Xin’s tower).

These two moments will—given the values we’ll choose for our key variables—occur one week apart. From a design standpoint, this works in our favor, as the ambiguity in which of these two key moments marks the completion of Tenaris Xin’s ritual offers the DM a means of either giving the PCs an extra week of time to succeed in their quest (if they’ve made slow progress), or not (if they’ve made good time). ⇑

4 And—strictly as a bonus for very clever players—if they manage to deduce the hyperdimensional structure of Lacc’s incursion, the players can work out the way in which the expansion rate of the three intrusion zones depends on the geometric layout of the Gates, the tower, and the spatial separation distance between the two planes of existence. The success of the PCs should in no way depend on making this leap; it exists only as a reward for players who wish to unravel the puzzle, to reinforce the sense of underlying order and logical coherence which is created by the existence of the mystery in the first place. ⇑

5 Unlike the spatial separation distance, there is no need to justify the growth rate coefficient in any “in-universe” way. It’s well known that our own universe is full of such essentially arbitrary constants, which have the values that they have for no reason other than “that’s just the way it happens to be”. One may appeal to anthropic reasoning to justify some such values, but philosophical points like this are epiphenomenal with respect to our design considerations here.

Of course, another option is to stipulate that this value is not some universal constant but rather a variable, which may depend on any number of factors, from the mystical to the logistical. Perhaps Lacc’s intrusion zones expand faster on worlds where a greater portion of the mortal population are sinners or evildoers, making {$k$} a sort of (inverse) measure of a world’s aggregate righteousness. Or perhaps the Gates, and Lacc’s expansion, must be powered by the souls of the damned, which Xin sources from fiendish contacts in the Lower Planes, exposing Lacc’s incursion timeline to supply-chain disruptions caused by current events in the Blood War. One may derive an endless variety of plot hooks from such free variables. ⇑

This essay was originally posted on 2016-01-12.

I.

Patterns crystallize in strange ways.

Have you ever had a conversation like this?

Person A is leaving the house; person B notices.
B: Hey, where are you going?
A: Hm? Why?
B: What, you can’t tell me?
A: Why do you ask, though?
B: Oh, well, if you were going to <place>, I was going to ask you to do something on the way, but if you’re not going there then never mind…

(Variants include “what are you doing tomorrow” / “oh in that case you’ll have time to do something for me”, “what are your plans this Saturday” / “oh well if you’re free then you can come help me with something”, “are you planning to do <thing X>” / “oh in that case you can do something for me while you’re at it”, etc.)

As person A in this conversation, you might be tempted to reply (as I often am) along these lines:

“Look, if you want me to do something for for you, just ask me to do that thing. I’ll decide whether it’s on the way, whether it’s convenient, whether it’ll be ‘no bother’, and so forth. If it’s not, I’ll tell you; I’m an adult, I’m capable of saying ‘no’. Or maybe it’s not on the way, but I’ll decide to do it anyway. In any case, it’s my decision; don’t try to make it for me! Don’t interrogate me about my plans; they’re none of your business. Tell me what it is you want, and I’ll decide what I’ll do about it.”

But maybe I’m just a curmudgeon.

II.

The Law of Demeter (a.k.a. the principle of least knowledge) is a concept in object-oriented software design. It says that an object should have limited knowledge about other objects, and shouldn’t know anything about the inner workings of other objects (as opposed to their behavior). The Law of Demeter is closely related to the “tell, don’t ask” principle—the idea that an object in a program should tell another object what to do, rather than requesting some component of the second object’s implementation or internal state, then doing something directly using that “borrowed” component. (If one object provides another object with access to its inner workings, who knows what the other object might do with that access?)

The Law has been stated and explained in many ways. One oft-encountered analogy involves a paperboy who wants to get paid for delivering the newspaper. Should the paperboy reach into the customer’s pocket, pull out the wallet contained therein, and take some cash right out of said wallet?

Of course not. The paperboy tells the customer to pay him, and the customer pulls out his own wallet, takes out some cash, and hands it to the paperboy. Or maybe he goes and gets some cash from under his mattress instead. Or maybe he asks his wife for cash, because she handles the finances in the family. None of this is the paperboy’s business; he simply does not need to know anything beyond the fact that he asks for payment, and he gets paid. (After all, if the customer just hands the wallet over to the paperboy, who knows what the paperboy might do with it? Take out more money than he ought to get, maybe! We just don’t know; and trusting the matter to the paperboy’s honesty and judgment is foolish in the extreme.)

What implications the Law of Demeter has in actual software engineering practice is a matter of much discussion. But reading some of that discussion reminded me of that conversation from part I. And then… well, everyone knows that generalizing from one example is bad; but once you’ve got two examples, you’ve got a hammer pattern.

III.

In the comments section of Scott Alexander’s recent post on gun control, commenter onyomi talks about pro-gun-control arguments of the form “do you really need <insert some form of rifle or other “powerful” firearm>?”:

See, I just hate seeing a policy debate framed in terms of what the citizen “needs.” The question should be, “is there a really good reason to restrict a citizen’s presumptive right to buy whatever he wants in this particular case?” rather than “do you need this?” If you want it, are willing to pay for it, and there’s no very pressing reason why you shouldn’t be allowed to have it, then you should be allowed to have it. The question of “need” shouldn’t even arise.

I sympathize with this view. If I encountered an argument like that—“do you really need …?”—I might be tempted to reply along these lines:

“It’s none of your damn business what I do or don’t ‘need’. If you want to ban me from owning something, or doing something, well—make a positive claim that I shouldn’t be allowed to have or do that thing, make a case in support of that claim, and we’ll go from there. But I am certainly not obligated to stand for an interrogation about what I ‘need’. In any free society, and certainly in the United States, the default is that I have a right to do and to own whatever I damn well please, without having to explain or justify myself to anyone. If you want to curtail that right somehow, the responsibility is on you, the advocate for state intervention, to demonstrate to my satisfaction (or, to put it another way, to the public’s satisfaction) that this curtailment is necessary or desirable—not on me, the citizen, to prove to you that it’s not. Make your case, and I might even agree with you! Certainly I don’t think that people should be allowed to do just anything; I’m not an anarchist. But you don’t get to start the conversation by demanding an account of what I ‘need’.”

This isn’t an argument against gun control. Even if you agree with every letter of my hypothetical reply, the question of gun rights is not settled thereby. This is a response to one class of argument: the sort that demands access to my internal state, and then bases further arguments on the basis of that revealed internal state. My view is that once I’ve agreed to discuss with you the question of what decisions or conclusions should follow from this or that aspect of my internal state, I’ve lost—regardless of what side of the debate I’m on. Instead, I reject the presumption that my internal state is any of your business.

IV.

Tabletop role-playing games are notoriously rife with quasi-religious debates about the Right Way To Play. One such dispute concerns the concept of the so-called “mother, may I” style of play. The question at issue is, what determines what your character can do? Different games, different game-masters (GMs), and different gaming groups or communities have answered this question in various ways. (Often, different aspects of the same game system answer this question in ways that fall on different places along the spectrum of possible answers.) But roughly speaking, any answer to this question falls into one of two categories.

In one camp are the people who say: here are the rules. These rules fully describe what options are available to your character—what actions you can take, how your character can develop, what exists in the game world, exactly what happens when your character takes this or that action, and so forth. If you want to do something that isn’t covered by the rules—too bad; you can’t. No pleading or argument will let you step outside what the rules allow. But within the rules, you’re free to do as you like; no further restrictions are placed upon you. Even if the GM doesn’t like it, “the rules is the rules”—no special treatment for anyone.

The people in the other camp think that “the rules is the rules” is fundamentally too restrictive; it stifles players’ creativity, and places artificial limitations on characters’ actions that may make no sense within the logic of the game world. Also in this camp are GMs who don’t like being rigid and inflexible, or who pride themselves on being able to improvise and invent ways to handle anything their players can dream up, as well as those GMs who feel that their role is to make the players’ desires and intentions happen, rather than to be computers who faithfully implement the rules as written. Players who don’t like being told that their character can’t do something that they think they should be able to, and those who enjoy coming up with unusual, bizarre, or creative plans and solutions, according to their own model of the game world and the situations in it (even when that model contradicts the game rules), are in this camp as well.

The answer to the “what can a character do” question that’s espoused by those in the latter camp is: describe to the GM what you want your character to accomplish. He’ll tell you if it’s possible or not, and he’ll decide what happens if your character tries to do that thing. The GM decides how the game world reacts to your character’s actions, the details of how your abilities work, and so forth. The rules, whatever they may say, are not a straitjacket; they’re guidelines, perhaps, or suggestions—and you’re not limited by them. Your character can, at least in principle, do whatever you can think of; tell the GM what you want to accomplish or what sort of action you want to take, and if it’s something that makes sense, or if the GM agrees that your character should be able to do that thing, then you can do it. Likewise, the GM will determine, and tell you, how your character can accomplish what you’re trying to do, and what the results will be, and so forth.

The term “mother, may I?” is a derogatory description of the latter approach, encapsulating a criticism of that approach that’s often made by those in the former camp. The criticism is this: yes, the rules no longer limit you. But neither do they shield, empower, or inform you. Now, you’re at the mercy of the GM’s whim. Before, the challenge was: can you figure out how to accomplish what you want to do, with these known rules, which are laid out before you and will not be altered? Now, the challenge is otherwise: can you persuade the GM—no computer he, but a fickle human, whose mind is full of biases, strange notions, and moods which the winds of chance, or last night’s ill-digested pizza, might sway this way or that—of your plan’s reasonableness? Before, you could confidently say: “My character does this-and-such, as the rules clearly say that he can”. Now, you’re the child who beseeches the GM to permit your actions: “Mother, may I…?”

“Hmm, and what is it you’re trying to accomplish? What’s your goal?” asks the GM. You must explain, as the GM listens and nods, and judges whether he wants your plan to succeed or fail, whether your goals shall be accomplished or whether your designs shall be frustrated, according to his own inscrutable design; and on that basis, he decides what options for action he will permit your character to have. Even if he does allow your character to do what you ask him to permit, the consequences of that action are decided not by any mechanism which you may inspect, and whose workings you can master, but by the GM—by the unpredictable goings-on inside his mind, which determine whether your plan “makes sense” to him—a determination which is quite beyond your control. You can attempt to convince him, of course. You can plead your case—not by mere reference to the rules, no! they’re only suggestions now, after all, and may be overruled as the GM pleases—but by vague and dubious appeals to “common sense”, ill-defined principles of dubious applicability (from game design, physics, personal experience, or just about any other source you can pull in), tangentially related “facts” of questionable accuracy, emotional arguments about what you want and what’s “important to the character concept”, and anything else you can think of. If it works—if it gets the GM to adopt your view—it’s fair game.

When “mother, may I?” reigns, you don’t know what your options really are. Those options might change from day to day. You don’t know how the game world really works (because it works in whatever way “makes sense” to the GM, who is no longer bound by those same rigid rules which you discarded in your pursuit of greater freedom). And the game is no longer a cognitive challenge, an exercise in creativity, strategic thinking, understanding and mastery of complex systems, and all the other sorts of challenges that TTRPGs excel at providing. Now, it’s a game of persuasion, of manipulation, of phrasing your pleas in the right way (or just being louder and more insistent). How droll.

That’s the argument, anyway. Of course, in practice, no sensible gamer takes either view to its extreme, nor takes the same position on the spectrum in every single situation. But at the heart of this conflict of two philosophies of game design is the same sort of thing as in the examples given in the previous parts. Instead of simply being told—what someone wants from you, what you must do, what is legal, what is allowed—you’re asked to open up your internal state for inspection and judgment. Your interlocutor refuses to provide well-defined rules, binding upon you and him both. Instead, he demands that you tell him all about your plans, your needs, your intentions, your inner workings; then, he says, he’ll make his decision—on the basis of a decision procedure that he, and not you, will carry out.

In the RPG case, gamers with views closer to the “rules is the rules” end of the spectrum may respond to such demands along these lines: “Look, it’s none of your business what my intentions are, or what I’m trying to accomplish. My plans are my own; my internal state is not available for your viewing. I have no interest in attempting to convince you that you should permit me to do what I want to do; don’t ask me to justify why you should allow me to take this or that action. Describe the world; tell me what the rules are; and I’ll decide on a course of action.”

V.

Of course, devotees of role-playing games aren’t the only people to prefer rigid, known-in-advance rules over the chance to secure an ideal outcome by persuading a human decision-maker that they deserve it. Legal scholars and rationalists alike have recognized the value of stare decisis, or the notion of precedent—that the courts should not (at least, barring extraordinary circumstances) make decisions that contradict previous decisions made by other courts in similar cases.¹ Why have such a principle? Surely a more context-sensitive approach would be better? Even “similar” cases differ in details, after all, and may involve different people, who come from different backgrounds, etc.; shouldn’t judges evaluate each case in isolation, and make whatever decision seems most appropriate to the circumstance?

A similar question may be asked about the concept of equality before the law. Why should people be equal before the law? Aren’t different people… different? Shouldn’t a judge treat every person who appears before them as distinct individuals, rendering whatever decisions seem most appropriate to the circumstances—regardless of how other courts (or even the same court) may have treated other people in “similar” cases?

I leave it to others to explain the value of the law’s predictability, and its effect on freedom of self-determination. Links between stare decisis and the psychology of motivation, too, would make fertile ground for blog posts, and the essay on the implications of both said topics for the design of user interfaces is practically written in my head already—but that is a matter for another day. Right now, I’ll just say that contextualism—the view, described above, that says we should judge legal cases on an individual basis, and that opposes the principles of both precedent and legal equality—inevitably requires exposure of the petitioner’s internal state. For one thing, it’s simply a competitive advantage: someone who bares their heart to the (precedent-rejecting, context-embracing) arbiter of their fate will often have a better shot at a favorable outcome than someone who won’t—we humans are suckers for a sob story, we sympathize more when we relate better, we relate better when we feel that we know someone better, and so on… But even more: the arbiter will demand it, will demand explanations, justification, an account of intent, belief, and mental state, a claim of needs and a convincing case for them… because how else can you fully grasp the context of a matter? In short, if we commit to judging every case on its own merits, and taking full view of the unique, individual situation that surrounds it, then we will find ourselves saying: you who stand before us—give us full access to your internal state, that we may inspect and judge it.

VI.

One may wonder what comes of having such a system. Maybe it’s nothing bad? Isn’t being open a good thing, in general? Open source, open borders, open bars… seems legit. Why not throw open the shutters of our hearts? Why shouldn’t other people have access to our internal state? Ok, if not literally everyone, then at least people who have power over us, who make decisions that affect us—shouldn’t they have all the information?

“Those people might be bad people! They might maliciously use this privileged access for bad purposes!” Yeah, that’s true. But let’s not stop at the easy answer. Let’s say we trust that those who stand in judgment over us are good people, who have the best intentions. Perhaps we should tell them everything about ourselves—present an account of our needs, say—and let them decide what we should get, and what we should do. What comes of this?

“Well, there was something that happened at that plant where I worked for twenty years. It was when the old man died and his heirs took over. There were three of them, two sons and a daughter, and they brought a new plan to run the factory. … The plan was that everybody in the factory would work according to his ability, but would be paid according to his need. …

“It took us just one meeting to discover that we had become beggars—rotten, whining, sniveling beggars, all of us, because no man could claim his pay as his rightful earning, he had no rights and no earnings, his work didn’t belong to him, it belonged to ‘the family’, and they owed him nothing in return, and the only claim he had on them was his ‘need’—so he had to beg in public for relief from his needs, like any lousy moocher, listing all his troubles and miseries, down to his patched drawers and his wife’s head colds, hoping that ‘the family’ would throw him the alms. He had to claim miseries, because it’s miseries, not work, that had become the coin of the realm—so it turned into a contest between six thousand panhandlers, each claiming that his need was worse than his brother’s. How else could it be done? Do you care to guess what happened, what sort of men kept quiet, feeling shame, and what sort got away with the jackpot?” …

“Any man who tried to play straight, had to refuse himself everything. He lost his taste for any pleasure, he hated to smoke a nickel’s worth of tobacco or chew a stick of gum, worrying whether somebody had more need for that nickel. He felt ashamed of every mouthful of food he swallowed, wondering whose weary nights of overtime had paid for it, knowing that his food was not his by right, miserably wishing to be cheated rather than to cheat, to be a sucker, but not a blood-sucker. He wouldn’t marry, he wouldn’t help his folks back home, he wouldn’t put an extra burden on ‘the family.’ Besides, if he still had some sort of sense of responsibility, he couldn’t marry or bring children into the world, when he could plan nothing, promise nothing, count on nothing. But the shiftless and irresponsible had a field day of it. They bred babies, they got girls into trouble, they dragged in every worthless relative they had from all over the country, every unmarried pregnant sister, for an extra ‘disability allowance,’ they got more sicknesses than any doctor could disprove, they ruined their clothing, their furniture, their homes—what the hell, ‘the family’ was paying for it! They found more ways of getting in ‘need’ than the rest of us could ever imagine—they developed a special skill for it, which was the only ability they showed. …

“We were a pretty decent bunch of fellows when we started. There weren’t many chiselers among us. We knew our jobs and we were proud of it and we worked for the best factory in the country, where old man Starnes hired nothing but the pick of the country’s labor. Within one year under the new plan, there wasn’t an honest man left among us. That was the evil, the sort of hell-horror evil that preachers used to scare you with, but you never thought to see alive. Not that the plan encouraged a few bastards, but that it turned decent people into bastards, and there was nothing else that it could do—and it was called a moral ideal!”²

(Don’t let the talk about the “shiftless and irresponsible” distract you. Change happens at the margins; you get what you incentivize. And as usual, the greatest enemy is not around us, but within us.)

VII.

So maybe it takes a contrarian and malcontent like me to see this pattern in the sort of conversation described in Part I (a fairly innocent exchange, all things considered), but clearly, many people have noticed it in lots of other places, and they seem to take a rather dim view of it. The interesting question is, why does anyone not object to this sort of thing? Why does “I demand to know all about your internal state” ever work?

Our as-yet-unnamed pattern is a certain sort of illusion—a thing that masquerades as its opposite. The one offers you a bargain: “Open yourself up to me—give me information about yourself, allow me access to your inner workings, your internal state—and I will control you less.” Less? “Sure—if I know more about you, I can make less onerous demands; I can ask for only what you’re able to give; I can restrict you less, changing the rules so that they don’t prevent you from doing what you want to do; I can make sure your needs are met, as much as possible. In doing these things, I’ll be relieving your hardships, easing your burdens.”

In short, you’re offered greater freedom. But in every case, it’s an illusion. By surrendering the secrecy of your internal state, you make yourself less free, not more; though it may not always be obvious how.

What motivates the conversation described in Part I? Person B wishes to promote illusion that their request isn’t really an imposition at all, that person A is doing them a very minor favor, at best. After all, if you’ve revealed your internal state to me, I can now judge for myself what is or isn’t an imposition for you, and what costs you bear for doing what I want you to do, and whether those costs are reasonable. You can argue with me, dispute my judgments; but by doing so, you tacitly admit that this is now a matter that we have to settle by debate. You’re no longer sole authority on what you may reasonably be asked to do, and what you ask in return; now I may weigh in also.

In the RPG case, the game-master who says “Tell me what you want to accomplish, what your intentions and goals are, and I’ll decide whether that’s possible and allowed, and how you can do it”—is he giving his players more freedom, as he might claim? With the flexible “cooperation” of the GM replacing the cold and rigid rules, the players are much less limited! No; rather, the GM gives himself more power—the power to shape the game world according to whim, the power to decide at each step and level whether the players’ plans succeed or fail, where otherwise they might fairly win, surprising him with their cleverness and cunning, their success assured by the rules.

And in our other examples, you might gain the chance to secure a better outcome (if your powers of persuasion are good enough) than you would if the arbiter were systematic and impartial—but now your obligation to make your internal state available for judgment binds you like a set of chains. And what have you really gained? Today the outcome might be favorable, but tomorrow I might alter my accounting of what conclusions or decisions follow from what you’ve revealed, and your fate reverses. Or, with your inner workings laid bare for my inspection, perhaps I might decide that those inner workings are objectionable somehow. Tell me what your needs are, and perhaps I’ll judge that you shouldn’t have such needs—no one ought to have such needs. You’re not even back at square one, then; it’s much worse than that. Rather than chafing under rules that tell you what to do, you’re now given rules about whom to be.³

VIII.

But there’s another sort of cost to abandoning encapsulation.

Once I reveal my internal state you—once I report my plans and intentions to you, once I present an account of my needs, once I submit the details of my life for your inspection—I lock myself down, on all of the things I’ve revealed. The fact that you are basing decisions—ones that affect my life, and perhaps the lives of others—on what I’ve revealed to you, exerts pressure on me, to be exactly that way, to conform to what I’ve revealed, not to deviate, not to change. If you’ve only based your weekend plans on what I’ve let you see, the pressure comes from the threat of mild social disapproval, and I am constrained only in a minor way—but constrained nonetheless. If my internal state forms the basis for decisions about legal cases, or the distribution of resources, or national policy—then I am hard pressed indeed, and loss of freedom I suffer thereby is great, much greater than the imposition from all but the most draconian of laws. There are few freedoms as vital as the freedom to change one’s mind.

Of course, programmers have known about this for some time. Thus the Law of Demeter—because my internal state is none of your business.

The idea of “different views on the same data” is crucial. It’s ubiquitous in desktop applications—so much so that we forget about it—the proverbial water to the proverbial fish. It’s not nearly as common in modern web apps as it should be. Here are some examples, that we may better grasp just how basic and fundamental this concept is.

Example one: Finder windows

Note for non-Mac-users: the Finder is the graphical file manager on the Mac OS. (It also does other things, but that's the part of its role that we're concerned with here.)

In all of the examples in this section, the data is the same: “what files are in this folder?” Let’s look at some of the possible views onto this kind of data.

Figures 1–4 show the same folder in each of the four different available view modes: list, icon, column, and cover flow.

Figure 1. Finder window in list view. Miscellaneous files.

Figure 2. Finder window in icon view. Miscellaneous files.

Let's play a game of “spot the difference” between Fig. 1 (list view) and Fig. 2 (icon view). Here we're not concerned with visual differences, but with UX differences. Here's a partial list:

(1) List view shows more metadata. (Here we see modification date, size, type; view options allow us to show more/other columns, like date added, version, tags, etc.)

Does the icon view show no metadata at all? Nope, it shows at least one piece of metadata: the file type—via the file icon. (This is an example of multiplexing; the icon has to be something—to provide a visual representation of a file, and to provide a click target—so why not multiplex file-type data into it?)

Of course, the icon is also visible in list view (but smaller); this means that in list view, file type is conveyed twice (if the “Kind” column is enabled). This is an example of redundancy in UI design, and of good use of sensory (in this case, visual) bandwidth (of which there is quite a lot!). Notice that this redundancy affords the UI a degree of freedom it would not otherwise have: the “Kind” column can be turned off (making room for other data columns, or allowing the window to be made smaller, to make room for other stuff on the screen) with minimal loss of information throughput for the UI.

But wait! What about the file name? There's metadata lurking there, too—the file type again, encoded this time in the file extension. Redundancy again; the file type is therefore displayed in three ways in list view (“Kind” column, icon, file extension) and in two ways in icon view (icon, file extension).

All of this gives the UI several degrees of freedom. How is this freedom spent? In at least two ways:

1. To allow for one or more of the channels through which file type information is communicated to be disabled or repurposed in certain circumstances, with minimal loss of information. (An example of a disabled channel: the “Kind” column is absent in icon view, but file type information is still visible. For an example of a repurposed channel, see the notes on Figures 5–9, below.)
2. To compensate for unreliability of some or all of the channels through which file type information is communicated. Sources of unreliability include:
   • The Finder may not recognize some obscure file types (the “Kind” column would then display no useful information); the file extension may be the only source of file type data in this case
   • The file extension may be missing (but Finder attributes may be set, thus allowing an appropriate icon to be shown and an appropriate value to be displayed in the “Kind” column)
   • The file icon channel may be repurposed (Again, see the notes on Figures 5–9, below, for an example)

(2) List view allows sorting. (Click on a column name to sort by that column's value; click again to reverse the sort order.)

… or is this really a difference? Actually, files can be sorted in icon view as well (there is both a “one-time sort” option and a “keep sorted by…” option). This is not obvious, because the UI for sorting in icon view is not discoverable by mere physical inspection, whereas in list view the column headers are visible, the sort order indicator is visible (the triangle, pointing up or down), and the “click column header to sort tabular data by that column's value” is a well-known idiom. (In icon view, sorting is done via a menu—either from the menubar, or from the context menu, or from a menu in the window toolbar.)

There is, however, a more subtle difference: in icon view it is not possible to sort in reverse order. Why not? The only reason is that Apple was unable (or unmotivated) to design a good UI for reversing sort order in icon view.

General lessons:

• The same (or analogous) forms of interaction with the data may be implemented via different UI designs in one view vs. another view.
• If the UX for a particular interaction in one view is obvious, don't assume that in other views it's impossible to design and implement.
• However, not all interactions that are possible in one view need to be (or can be) available in all views. (It makes little sense to provide “one-time sort” functionality in list view.)

Design principles:

1. In each view, provide as many interactions as is reasonable, no more and no less. (Provide more and you clutter and complicate the UI; provide fewer and some or all of the views will be too capability-poor to be useful.)
2. Strive to have each view provide as complete a set of interactions with the data as possible.
3. To reconcile the tension between the above two design principles, remember that it's better to provide a capability and hide it away behind a non-obvious or non-trivial-to-discover UI than not to provide it at all. This way, it will be available for power users but will not trouble less experienced users. (Of course, this is not an excuse to hide capabilities behind non-obvious UIs when there's a good reason, and a good way, to provide an easily-discoverable UI for them.)
4. At the same time, look for ways to exploit the unique properties of each view to provide additional interactions that would impossible or nonsensical in other views.
5. The more ways the user can interact with the data, the better.

(3) Icon view allows arbitrary grouping and arrangement; I can position the files in the window wherever I like (example 1, example 2, example 3, example 4, example 5).

(Unless a “keep sorted by…” option is enabled.)

Some file managers don't have this feature; the Finder does. The lesson:

Do not carry over UX/interaction limitations necessitated by one view, to another view where they are not necessary.

Arbitrary grouping and arrangement makes little sense in list view. In icon view, there's no reason not to permit it—except, of course, that allowing the user to set, and then tracking, arbitrary icon positions, takes work! Does it offer a benefit? Find out! Ask users, survey other implementations, etc. In general, users resent limitations on their freedom, and appreciate the lack of them.

(4) What aspect(s) of the data may be easily gleaned via visual inspection differs from one view to another.

Different views (usually) look different. It's easy to forget this, but it's crucial. Here (in the “Finder list view vs. Finder icon view” example) this manifests in a couple of ways:

1. In list view, it's easier to pick out files which differ from the others in any displayed metadata value (modification date, file name, etc.). This is true not only due to the sort feature, but also because humans find it easy to scan down a list of text items (which are horizontally aligned) and notice ones which stand out.
2. In icon view, the "file icon" data channel is wider (because the icon is displayed at a larger size); more data is coming through this channel. This makes it easier to distinguish icons, but also allows this channel to be used for other purposes (see notes on Figures 5–9, below).

General lessons:

For humans, the visual channel is a high-bandwidth one. Use it. Some ways to optimize UI visual bandwidth:

• Multiplex meaning.
• Allow the repurposing of high-bandwidth components.
• Remove obstacles to visual apprehension of patterns (minimize "non-data ink", etc.).
• Assist the brain's pattern-recognition abilities by using alignment, contrast, repetition, and proximity cues.

The same folder as in Fig. 1 and Fig. 2, but now in column view (Fig. 3) and cover flow view (Fig. 4):

Figure 3. Finder window in column view. Miscellaneous files.

Figure 4. Finder window in cover flow view. Miscellaneous files.

Figure 5. Finder window in icon view. Folder containing low-resolution icons.

Figure 6. Finder window in list view. Folder containing low-resolution icons.

Figure 7. Finder window in list view. Folder containing high-resolution icons.

Figure 8. Finder window in icon view. Folder containing high-resolution icons.

Figure 9. Finder window in icon view, zoomed to cover most of desktop. Folder containing high-resolution icons.

Figure 10. Finder window in list view. Miscellaneous files. No toolbar.

Figure 11. Finder window in list view. Miscellaneous files. One folder expanded to depth 1.

Figure 12. Finder window in list view. Miscellaneous files. One folder fully expanded.

Example two: Microsoft Word document windows

Figure 13. Word document window in draft view.

Figure 14. Word document window in print layout view.

Example three: structured data

1. A .csv file, displayed as plain text
2. The same .csv file, opened in Excel
3. An HTML file, containing the same data, plus markup such that the data will be displayed in tabular form, displayed as plain text
4. The same HTML file, rendered in a browser

(Analysis of examples two and three left as exercise for the reader.)

I’ve never seen this concept named, or concisely articulated, anywhere else. The idea itself is not original to me, of course.

Of any skill, or any domain where expertise of execution may be gained, there are three levels of mastery.

At the zeroth level, you break the rules, because you do not know the rules. Success is accidental; failure is likely; excellence, all but impossible.

At the first level, you know the rules, and follow them. You do well enough, though excellence is unlikely.

At the second level, you know, not just the rules, but the motivations behind them; you understand why the rules must be as they are. You follow the rules or break them, as the task demands; your actions are governed by deep principles. Success is near-effortless; excellence becomes possible, and even likely.

To achieve greater mastery, you cannot skip levels. At the zeroth level, you may look at one who has achieved the second level of mastery, and note that he routinely breaks the very rules he has instructed you to follow. Are there no rules, then? But there are; and they exist for good reasons. You will not achieve the second level of mastery before the first.

Likewise, the one who has achieved the second level of mastery says to him who has yet to achieve the first: “Do as I say, not as I do”. This is not hypocrisy. One who does not understand the three levels may think: “He is allowed to break the rules, as I am not, because of some privilege of rank”. But it is only that to think outside the box, you must know the shape of the box, its contours; if you cannot see the box, you will never escape it.

And once more: you cannot explore the space of possibilities, if you do not know its dimensions. The axes of that space are not the bars of a cage, but signposts; not seeing them, you are not infinitely free—but only doomed to wander forever in a Flatland of amorphous mediocrity.

There’s a small-ish cluster of serif fonts—all of recent design, not digitizations of classic typefaces, nor even designed for (professional) print¹—that people always have trouble fitting into one of the traditional categories of serif typefaces.

In appearance, it looks something like if Baskerville, a 225-year-old typeface that has been shown to shape our perception of truth, and Caecilia made a baby.

The Kindle Finally Gets Typography That Doesn’t Suck

These fonts are sort of like transitional serifs, but they’re also sort of like slab serifs, and sometimes they’re called “transitional serif but with features of a slab serif”² etc. etc.

… a crisp, modern serif typeface … avoids the stuffiness of historical text faces and doesn’t overreach when it comes to contemporary detailing … a balanced, low-contrast typeface with economic proportions…

Elena font description

Fonts in this category share these properties:

• fairly thick strokes in the normal weight
• low stroke weight variation
• serifs that are not sharply tapering nor thin and dainty, but thick (yet not geometric or square, as slab serifs)
• relatively open counters
• relatively large x-heights

… simply a contemporary body text font.

Tuna font description

Fonts in this category include:

• Charter
• Source Serif Pro
• Equity
• Chaparral Pro

… and quite a few more more—see the full list (that I’ve found so far) on my wiki (and feel free to suggest additions on the Talk page!).

Some samples:

The category does not seem to have any accepted name³—yet unquestionably this is a real cluster in font-space. This blog post is meant to call attention to the cluster’s existence.

The characteristics listed above mean that fonts like this will render well across a variety of environments, software and hardware. And empirically, these fonts make for pleasing and readable body text on the web. So, at least for now (unless and until someone tells me that there’s already an accepted name), I’m calling these fonts “screen serif” fonts.

If you want your pages to be readable and attractive, try setting your body text in one of these fonts! (Again, check out my wiki for the full list—I’ll be adding more “screen serif” fonts to it as I come across them.)

SimTower was an elevator simulation game.

OK, it actually had other things in it, not just elevators. But the elevators were the heart of it—they were the most engaging part of the gameplay, with the most complex game mechanics—and, more than anything else, it was mastery of the elevator design that would bring a player success in SimTower.

I played SimTower a lot when I was younger. Read more...